Оптический способ оценки поверхностных повреждений

Ограниченные возможности традиционных механических и оптических методов оценки поверхностных повреждений (невозможность проведения исследования в условиях эксплуатации без остановки оборудования и разборки изделий, низкая чувствительность измерений, сложность определения вида повреждения и др.) и случайный характер распределения самих повреждений и их параметров (глубина, угол раскрытия и расположение плоскости симметрии трещины, одновременное наличие различных видов повреждений и др.) требуют создания новых способов и испытательного оборудования для обнаружения дефектов поверхности. Преимуществами приборов, принцип действия которых основан на использовании лазерного излучения, являются бесконтактность, высокая информативность, быстродействие, возможность работы в реальном масштабе времени. Подобные измерительные приборы имеют существенное превосходство перед другими средствами контроля состояния поверхностей деталей и применяются для обнаружения поверхностных трещин, дефектов сварных швов и резьб, определения шероховатости и износа поверхности /1-2/.

В данной работе приводятся методика и результаты исследования зависимости отражательной способности конструкционных материалов от состояния поверхности, вида повреждений поверхностного слоя, энергетического соответствия пространственно-временных характеристик отраженного сигнала различным видам дефектов и влияния характеристик зондирующих лазерных пучков (диаметра пятна, угла падения излучения, длины волны, интенсивности источника излучения) на результаты измерений.

Переотражение излучения в измерительной системе

Для выявления зависимости величины отраженного сигнала от параметров оптической системы (диаметра пятна, угла падения излучения, диаметра приемного объектива) и геометрических параметров дефекта рассмотрим изменение интенсивности зеркально отраженного излучения при сканировании по

поверхности с трещиной произвольного угла раскрытия 2 у .

При распространении излучения точечного источника в трещине (рис.1) и постоянном коэффициенте отражения,

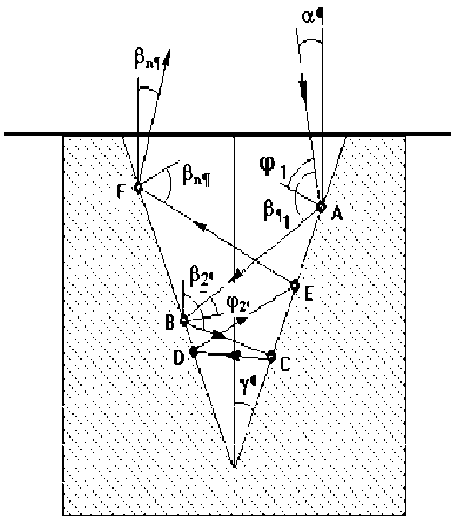
Рис. 1. Схема распространения излучения точечного источника в трещине.

П

Ф1 = - - а - Y в1 = 2ф1 + а = п- а - 2/ из треугольника АВО:

ПП

- - Ф1 + - + ф 2 + 2Y = П

П

ф 2 = -2Y + Ф1 = -а - 3Y + -

п в2 = у - Y + ф 2 = П - а - 4Y а для произвольного значения n:

вп = п - а- 2 nYф = у - а - (2 n -1)/

где а - угол падения излучения на исходную поверхность, ф 1 - угол падения излучения на поверхность трещины, Р 1 - угол между отраженным поверхностью трещины излучением и вертикалью при первом отражении, ф ₂, Р 2 - угол падения излучения и угол между отраженным лучом и вертикалью при втором отражении от поверхности трещины, ф _п, p n - угол падения излучения и угол между отраженным лучом и вертикалью при выходе из

трещины, у - половина угла раскрытия трещины, п -число переотражений излучения.

Отметим, что после отражения от поверхности трещины излучение идет вниз, если ф _п > 0 вверх если ф _п< 0.

Соотношение углов а и у , для которых направление распространения излучения на выходе из трещины, соответствует направлению зеркально отраженного от исходной поверхности излучения и определяется в случае р _п = а , у = ( п /2 - а )/п. При падении излучения источника с квадратным сечением с равномерным распределением мощности на поверхность с трещиной, когда приемный объектив также имеет квадратное сечение со стороной В₂ и расположен под углом Р к нормали к поверхности, значение x (смещение светового пятна относительно края трещины), при котором излучение, выходящее из трещины, попадает на приемный объектив, удовлетворяет неравенству:

H ₂ tg Y< x < H ₂ tg Y + В 1 / cos a (4) где H 2 =B 1 - глубина трещины. Момент, при котором отраженное трещиной излучение начинает попадать на объектив, соответствует x₁=x_, тогда максимальное значение отраженного трещиной излучения попадает на приемный объектив при x = 2H 2 tg y . Затем значение этой величины снижается и становится

Аналогичная картина распространения излучения в трещине будет наблюдаться, при всех четных значениях n и неизменном значении ширины трещины. Условие р _п = а также выполняется при уменьшении угла раскрытия трещины. Координаты x 1 и x 2 имеют те же значения, что и для n=2, угол выхода излучения из трещины р _п соответствует углу р ₂ при п=2. Значения W/W₀ определяются в соответствии с выражениями (5) и (6),во второе слагаемое вместо А₂² входит А₂ⁿ. При уменьшении угла раскрытия трещины данное условие выполняется при n=2 и увеличении значений углов а и р _п. Для нечетных значений n излучение выходит из трещины в направлении источника.

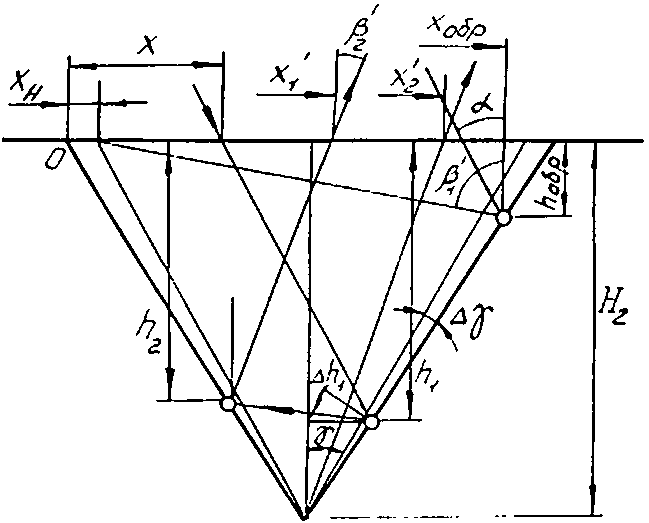
Рассмотрим случай, когда половина угла раскрытия трещины увеличивается на Ау (рис.2) и определим характеристики пучка, выходящего после переотражения из трещины при прежнем значении угла падения излучения а =30 0 и глубины трещины (Н₂ =В₁).

равным нулю, при x = H₂tg y + B₁/cos а .

Отношение величины сигнала W при наличии трещины к величине сигнала на бездефектной поверхности W 0, при п=2 для H₂tg y < x < 2H 2 tg y

определяется выражением:

- x 2/

W cos a      A 2 ( x - x 1 )

Wo =    B 1     + A 1 B 1

cos a cos a

а для H ₂ tg y ( x ( H ₂ tg Y + B 1 / cos a

A ₂ x ₂

W _ x - 2H2 tgY +   (

W 0

B 1

cos a

B 1

- I x--

I cos a

A 1 B 1

cos a

где А₂ - коэффициент отражения поверхности трещины, А₁ - коэффициент отражения бездефектной поверхности. При этом доля излучения, попавшего на объектив после переотражения в трещине для соотношения углов у = ( п /2 - а )/п, определяется координатой пятна x и не зависит от высоты расположения объектива над поверхностью Н₁.

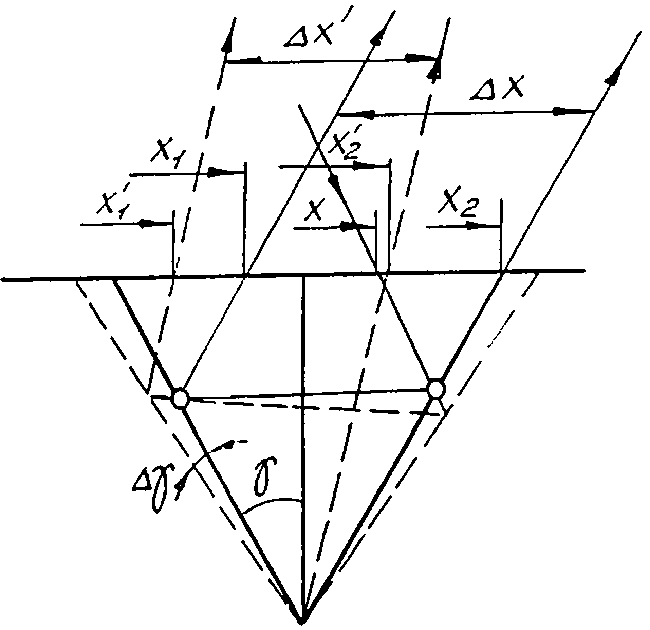
Рис. 2. Распространение излучения в трещине при увеличении угла раскрытия трещины на 2 Ау (а) и распространение излучения в трещинах с углами 2 у и 2( у + Ау ) (б).

В соответствии с условием (3), излучение выходит из трещины под углом Р 2 = Р 2 -4 Ау , Р 1 = Р ₁-2 Ау , Р 1 = п /2 - 2 Ау , а ширина выходящих из трещины пучков A x = x₂ - x₁, A x = x₂ - x₁. Здесь знак "" соответствует трещине с углом у + Ау . Если для трещины с углом у все излучение, попадающее в трещину, выходит из нее под углом р ₂, то для трещины с углом у + Ау под углом Р 2 = Р 2 -4 Ау распространяется излучение, попадающее в трещину при x_н< x < x_обр имеет следующие параметры: х_н= H₂tg( y + Ay ) -tg y , S =2H₂tg( y + Ay ), S/B 1 =2tg( y + Ay ). В частности, при Ау =3 0 S/B i = 1,3.

Определим значение xобр - координаты изменения направления сигнала:

xобр + hобрtga + hобрtg (/ + А/) =

= 2 H 2 (tg I/ + АУ)), hобр = (Хобр + hобр tga ^tg^i                   (7)

Тогда момент, когда излучение, выходящее из трещины, начинает попадать на приемный объектив, определится условием (рис.2):

D j( 0, D i = x j- x -

• - ( tg a - tg ^ X H i - 0,5 B i sin a ) ,

x j - x ( ( tg a - tg p ₂ X H 1 - 0,5 B_i sin a )           (8)

Излучение, выходящее из трещины, полностью попадает на приемный объектив при условии:

• D 2 ( 0, D jX

D j = x j- x + - B cos a

• -    ( tg a - tg p ₂ )( H 1 - 0,5 B_i sin a )

, f    Bi L xj -1 xI <

( cos a J

• <    ( tg a - tg p 2 X H i - 0,5 B i sin a )

D 2 = x 2 - x -

• -    ( tg a - tg p ₂ )( H _i - 0,5 B _i sin a )

x ^j- x (⁽ tg a - tg p 2 ) x                          (9)

x ( H _i - 0,5 B _i sin a )

Излучение выйдет за границы приемного объектива при условии:

D 2 ( 0,

D 2 = x 2 - x +—— cos a

• -    ( tg a - tg p ₂ )( H _i - 0,5 B _i sin a )

, f    Bi L x 2 -1 xI <

( cos a J                           (10)

• <    ( tg a - tg p 2 X H i - 0,5 B i sin a )

Соотношения (4), (5), (8) - (10) позволяют построить зависимости изменения относительной величины сигнала W/W0 от значения координаты x.

Экспериментальные результаты

Для экспериментального подтверждения теоретических зависимостей влияния формы трещины (угла раскрытия трещины и расположения плоскости симметрии трещины) на изменение интенсивности излучения, отраженного от поверхности использовался источник с равномерным распределением интенсивности излучения круглого сечения. Приемный объектив с круглым сечением устанавливался над исследуемой поверхностью на высоте H 1 , диаметр приемного объектива был равен диаметру источника излучения. Угол падения излучения составлял а =30 0 Угол a ₂ определял расположение плоскости наблюдения относительной исследуемой поверхности и был равен 0, если плоскость наблюдения перпендикулярна направлению распространения зеркально отраженного излучения от бездефектной поверхности. Относительная ширина трещины для всех случаев была равна S/D₂=1,15. Относительная глубина трещины S/H₂ изменялась в диапазоне S/H₂=0,65...1,44, S/H₂=0,65 соответствовала y =i8⁰, S/H₂=i,44 соответствовала y =35,8⁰ (S - ширина трещины,Н₂ - глубина трещины). Как показывают измерения, при а ₂=0⁰ и а = у относительная величина сигнала не зависела от высоты расположения приемного объектива над поверхностью, и при всех значениях H 1 кривая имела один и тот же вид. Здесь введены обозначения: у -угол раскрытия трещины, ф ₁- угол поворота плоскости симметрии трещины вокруг линии пересечения плоскости симметрии трещины с исходной поверхностью, ф ₂ - угол наклона плоскости симметрии трещины к плоскости, перпендикулярной данной плоскости. При S/D 2 >1 значения относительной величины сигнала W/W 2 не зависели от соотношения ширины трещины и диаметра пятна, вид кривой определялся конфигурацией трещины (значениями углов у , ф ₁ и ф ₂). При S/D₂<1 для той же трещины значения относительной величины сигнала W/W 0 возрастали, при S/D 2 ^ 0 W/W 0 ^ 1 для всех точек поверхности независимо от наличия дефектов, выявление трещин невозможно (этот вывод вытекает из зависимостей математической модели). Максимальное значение относительной величины сигнала на поверхности трещины при а = у соответствовало центру трещины (x/D₂ = =S/2D 2 + 1/2cos a ) и было равно при четном значении числа переотражений в трещине W/W₀ = A^(n-1), где А - коэффициент отражения поверхности трещины, n - число переот-ражений в трещине. При нечетных значениях n и п ^м (n>6,S/H₂<1) W/W₀ ^ 0 для указанного значения x/D 2 при S/D 2 >1.

При уменьшении угла раскрытия трещины максимум на кривой смещался в сторону приемного объектива. Величина максимума и его смещение за- висели от угла раскрытия и глубины трещины, а также расстояния от поверхности до приемного объектива.

Заметим, что изменение положения плоскости наблюдений ( α ₂ = 0⁰) оказывает существенное влияние на форму кривой W/W₀ . Для α = γ =30⁰ так же, как и при α ₂=0⁰, сохраняется значение относительной величины сигнала в максимуме и расположение максимума при всех значениях α 2 = 0⁰. Значение W/W 0 в точках, соответствующих прохождению центра пятна через края трещины (x/D 2 =0,577 и x/D₂=1,73) снижается с ростом α ₂. Для трещин с углами α - γ характерно появление максимумов при x/D 2 = 0,8...0,9, значение W/W 0 в максимуме возрастает с ростом α ₂, при x/D₂=1...1,6 наблюдается минимум, значение W/W 0 в этой точке снижается с ростом α ₂. Для γ =34⁰ максимальное значение W/W₀ =0,67 при x/D 2 =0,9 и W/W 0 =0 при x/D 2 =1,5 соответствуют α 2 =75⁰. Для γ =27⁰ и α 2 =75⁰ максимальное значение W/W 0 =0,85 при x/D 2 =0,83, W/W 0 =0 при x/D 2 =1,04.

Проведенные исследования показали, что расстояние от исследуемой поверхности до приемного объектива H₁ оказывает наибольшее влияние из всех параметров оптической системы на форму кривой W/W 0 . При H 1 /D 2 >>1 форма кривой не зависит от значений углов γ , ϕ ₁ и ϕ ₂ и определяется только шириной трещины S и соотношением ширины трещины и диаметра пятна S/D 2 . Соотношение S/D 2 не оказывает влияния на определение характера трещины при S/D 2 >1. При S/D 2 <1 для той же трещины значения относительной величины сигнала W/W 0 возрастают, при S/D 2 → 0 W/W 0 → 1 для всех точек поверхности независимо от наличия дефектов, выявление трещин невозможно. Поворот плоскости симметрии трещины (изменение величины угла ϕ 1 ) возможно выявить для неглубоких трещин (S/H 2 >1) при γ -( π /2 - α )/n и -5⁰< ϕ 1 <5⁰. При большем угле поворота трещины и для глубоких трещин значение угла ϕ 1 не влияет на форму кривой, так как излучение, переотраженное поверхностью трещины не попадает на приемный объектив. Наклон плоскости симметрии трещины (изменение величины угла ϕ 2 ) также приводит к смещению максимумов и минимумов на кривой сигнала измерений. Изменение положения плоскости наблюдения наиболее существенное влияние оказывает при γ - ( π /2 - α )/n. При α ₂-0⁰ и ϕ ₁=0⁰ и ϕ ₂=0⁰ появляются максимум в левой части кривой (x/D 2 <1) и минимум в правой части (x/D₂ → 1), с ростом α ₂ возрастает значение W/W₀ в максимуме и снижается значение W/W 0 в минимуме. Несмотря на большую чувствительность к изменению угла раскрытия трещины при α 2 = 0⁰, изменение ориентации плоскости наблюдения может привести к снижению разрешающей способности метода при α ₂ ≥ 45⁰, так как поворот плоскости наблюдения при неизменном значении размеров приемного объектива равносилен снижению его площади в плоскости α 2 =0.

Разработанное испытательное оборудование по обнаружению поверхностных дефектов по результатам измерения интенсивности отраженного лазерного излучения при сканировании по поверхности детали включает в свой состав гелийнеоновый лазер ЛГИ-224-1 ( λ =0,6328 мкм), стеклянную пластину для формирования опорного сигнала, два оптических ваттметра поглощаемой мощности ОМЗ-65 для регистрации сигналов опорного и измерительного каналов, плоские зеркала и собирающие линзы для направления излучения от источника к исследуемой поверхности и отраженного от поверхности излучения к фотоприемнику, устройство для перемещения образца. Величина опорного сигнала составляла ~ 6% от интенсивности источника излучения.

Были исследованы поверхности следующих образцов: из титанового сплава ВТ-14, из химически полированного алюминия АД-1М, из алюминиевого сплава АД-1М с покрытием на основе полисилоксанового масла, стеклотекстолита АФТ-2П. Профилограммы поверхностей образцов были записаны на профилографе завода "Калибр" модели 250.

Как показали исследования, резкое снижение интенсивности отраженного излучения на величину до 50...98% свидетельствует о наличии царапин, трещин и повреждения покрытий. Размеры дефекта определяются разностью координат, соответствующих резкому снижению сигнала и его возрастанию до прежнего уровня. Вероятность распознавания дефектов зависит от соотношения размеров пятна излучения на поверхности и дефекта, а также шага сканирования и размера дефекта. Распознавание дефекта невозможно, если его площадь значительно меньше площади сканирующей апертуры и шаг сканирования превышает размеры дефекта. Наибольшая вероятность распознавания дефекта достигается в том случае, если диаметр пятна излучения на поверхности не превышает размеров дефекта и равен шагу сканирования. Разброс величины сигнала W/ W₀ увеличивается с ростом шероховатости поверхности. Искривлению поверхности образца соответствует монотонное повышение или снижение величины сигнала W/W 0 c ростом координаты x/x 0 (образец из химически полированного алюминия с покрытием на основе полисилоксанового масла). Изменению шероховатости на участке поверхности образца соответствует изменение среднего уровня величины W/W 0 (образец из стеклотекстолита АФТ-2П; Ra=7,45 -W/W 0 =0,49; Ra=4,8 - W/W 0 =1,1).

Износ участка поверхности образца из титанового сплава ВТ14 характеризуется увеличением шероховатости и отклонением средней линии профиля, что соответствует снижению интенсивности излучения, отраженного от поверхности образца.

Наличие царапин, трещин и повреждений покрытий приводит к резкому снижению сигнала W/W0. Возможно также резкое увеличение интенсивности отраженного излучения (образец из стеклотекстолита). Наиболее сильное снижение сигнала отмечается при наличии трещин (W/W0≈0,03). Наличие воды на поверхности образца приводит к снижению среднего уровня сигнала W0, величина которого зависит от материала образца. Для образца из титанового сплава ВТ14 слой воды толщиной 1,5 мм приводит к снижению интенсивности излучения, отраженного от поверхности образца, в 2 раза. Наличие повреждения регистрируется так же, как и на сухой поверхности. При смачивании поверхности образца водой происходит смещение пятна излучения на фотодиоде, величина которого зависит от толщины слоя жидкости.

Существенное уменьшение габаритов испытательного оборудования возможно при использовании полупроводниковых лазеров в качестве источников излучения. Были проведены исследования их флуктуаций мощности, распределения плотности мощности и отклонения излучения в пространстве. Наиболее распространенными материалами для лазерных диодов являются кристаллы, полученные на основе GaAs и InP с активной областью на основе материалов тройных и четверных систем. Примерами таких лазеров являются GaAlAs/GaAl и AlGa-InP/InP лазерные диоды /3/. Преимуществами лазеров с четверной системой являются /4/: изопериодичность гетероструктуры и отсутствие температурных деформаций, связанных с несоответствием параметров решеток подложки и активной области; высокая оптическая прочность зеркал, отсутствие "дефектов темных линий", слабое участие дислокаций в процессе деградации и, вследствие этого, более высокая долговечность и выходная мощность; отсутствие изгибов на ватт-ам-перной характеристике и большая стабильность оси диаграммы направленности.

По сравнению с другими типами лазерных диодов лазеры с квантоворазмерными структурами имеют в 3 раза меньшее значение порогового тока и более высокое значение характеристической температуры (200К) и, следовательно, более слабую зависимость порогового тока и выходной мощности от температуры активной области и окружающей среды. Как показали исследования, они характеризуются отсутствием изгибов на ватт-амперной характеристике и более высокой дифференциальной эффективностью. Лазеры с квантоворазмерными структурами сохраняют одномодовый режим и длину волны генерации при накачке импульсным током высокой частоты.

Наиболее приемлемыми для использования в контрольно-измерительных системах являются лазерные диоды с квантоворазмерными структурами с активной областью на основе материалов четверных систем.

Заключение

Таким образом, построена математическая модель, описывающая изменение относительной величины сигнала W/W 0 от безразмерной координаты x/B 1 при сканировании по поверхности (B 1 -поперечное сечение источника излучения) при различных соотношениях значений углов α и γ (угла падения излучения и половины угла раскрытия трещины), когда размер поперечного сечения пучка и ширина трещины приблизительно равны (одного порядка), ∆γ < γ . На участке поверхности с наличием трещины кривая изменения относительной величины сигнала имеет максимум или минимум в зависимости от глубины трещины. Угол раскрытия трещины, при котором имеется максимум на кривой, зависит от коэффициента отражения поверхности и угла падения излучения. Теоретические и экспериментальные исследования показали, что расстояние от исследуемой поверхности до приемного объектива H 1 оказывает наибольшее влияние из всех параметров оптической системы на форму кривой W/W₀. Поворот плоскости симметрии трещины возможно выявить лишь для неглубоких трещин (S/H 2 >1) при -5⁰< ϕ 1 <5⁰, при большом угле поворота трещины и для глубоких трещин значение угла ϕ 1 не влияет на форму кривой. Наклон плоскости симметрии трещины приводит к смещению максимумов и минимумов на кривой отраженного сигнала. Изменение положения плоскости наблюдения приводит к появлению дополнительных максимумов и минимумов. Наиболее приемлемыми для использования в контрольно-измерительных системах являются лазерные диоды с квантоворазмерными структурами с активной областью на основе материалов четверных систем. Для учета флуктуаций мощности источника излучения в процессе измерений необходимо формирование опорного канала.