Оптический захват и перемещение микрочастиц с помощью асимметричных пучков Бесселя-Гаусса

В [1–4] рассмотрены непараксиальные асимметричные моды Бесселя (аБ-моды) и параксиальные асимметричные пучки Бесселя–Гаусса (аБГ), обладающие орбитальным угловым моментом (ОУМ). В поперечном сечении этих лазерных пучков распределение интенсивности имеет вид полумесяца. В [5] aБ-моды исследовались экспериментально с помощью цифровой матрицы микрозеркал. В [6] по аналогии с [2] (вводя комплексное смещение моды Бесселя) рассмотрены асимметричные пучки Чебышева–Бесселя. В [3–5] исследовалась также параксиальная фокусировка аБ-пучков. С другой стороны, известны векторные пучки Бесселя [7, 8], которые распространяются без дифракции и имеют различные состояния поляризации. В [7] показано, что бездифракционный линейно-поляризованный векторный пучок Бесселя выражается через ряды из функций Бесселя и имеет в своем спектре бесконечное число угловых гармоник. Векторные пучки Бесселя с азимутальной и радиальной поляризациями можно сформировать с помощью 4 конических поверхностей с углом Брюстера или 4 аксиконов [9]. Сфокусированный лазерный пучок с распределением интенсивности в виде полумесяца используется для оптического захвата и перемещения биологических микрообъектов [10]. Но данный пучок рассчитывается итеративно в параксиальном приближении, и его острая фокусировка в [10] не исследуется. Острая фокусировка аБГ-пучков исследовалась в [11].

В данной работе исследуется оптический захват, вращение и перемещение полистироловых микрошариков с помощью аБГ-пучков с разной степенью асимметрии. Экспериментально доказано, что при постоянном значении топологического заряда с ро-

стом степени асимметрии пучка растёт ОУМ лазерного аБГ-пучка и скорость перемещения микрочастиц вдоль искривлённой траектории этого пучка в поперечной плоскости.

1. Асимметричный пучок Бесселя–Гаусса

В [3,4] рассмотрен асимметричный пучок Бесселя–Гаусса:

E n ( r , ф , z ; c ) = 1exp ^q

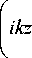
i a? z 2 kq

r2 .   L—- + inф |X q to     J

X

ar ar - 2 cq exp (i ф)

n 2

X

a r

2 cq exp ( i ф )^] } ,

который получается из обычного БГ-пучка [12]

„ ,      .    -w x |        ia2z |En(r,Ф,z) = q (z)expl ikz- ——- IX

(      2 kq ( z ) J

(    r2        I Г a r

^{X exp} l —ГТТ⁺ in ф I Jn —T , ( to o q ( z )        J L q ( z ) J

с помощью комплексного смещения моды Бесселя по декартовым координатам

, c

x = x, a ic

У = У —,

I a

где c – безразмерный параметр асимметрии, α = k sin θ 0 = (2 π /λ)sin θ 0 – масштабирующий множитель, k = 2 π /λ – волновое число света с длиной волны λ, θ 0 – угол конической волны, формирующей пучок Бессе-

ля, q(z) = 1 + iz/zo, z0 = кto0 /2 - длина Рэлея, too - радиус перетяжки Гауссова пучка, Jn(x) – функция Бесселя первого рода n-го порядка, n – топологический заряд пучка. Поле (1) формирует параксиальный асимметричный пучок Бесселя–Гаусса при любых целых n и любой комплексной постоянной с. Но для простоты в дальнейшем будем считать постоянную c вещественной положительной величиной: c ≥ 0. Хотя если рассмотреть c как комплексную величину c = |c|arg c или учесть, что она может быть отрицательной c <0, то распределение интенсивности поля (1) повернется на угол arg c вокруг оптической оси. На рис. 1 показано распределение интенсивности и фазы аБГ-пучка (1) при значении параметра асимметрии с, равном 10. При моделировании были исполь- зованы следующие значения параметров: длина волны X = 532 нм, радиус перетяжки Гауссова пучка too = 10X, масштабирующий множитель a = 1/(10X), границы расчётной области -40X < x, y < 40X.

а)

б)

Рис. 1. Распределение интенсивности (негатив) (а) и фазы (б) светового пучка (1) с топологическим зарядом n = 3 в начальной плоскости при z = 0 для с = 10

Угловой Фурье-спектр аБГ-пучка имеет вид [3,4]:

An ( р ,^ф ) = exp

к Р^юо Y  . _А

0   + in ф

• 2    f J *

  х

  
  

  5        ) n / ²

  5+ 2 ce< ^{ф-п /2)} J

  
  
  
  

х Ip {^ [5+2 ce(ф-/2) ]}, где 5 = а к ptoO /(2 f), In (x) - модифицированная функ- ция Бесселя. Угловой спектр (4) асимметричный: при φ = π/2 и на кольце фиксированного радиуса ρ = ρ0 модуль амплитуды (4) имеет максимум, а при φ = -π/2 – минимум. Вид углового спектра (4) похож на вид амплитуды аБГ-пучка (1) (с точностью до замены функции Бесселя модифицированной функцией Бесселя), но повернут на 90 градусов. Поэтому асимметрия спектра (4) похожа на асимметрию аБГ-пучка (1).

Выражение для ОУМ, нормированного на интенсивность, имеет вид [3,4]:

Л=„ +У ^{c 2 PpI} " + p ⁽ y )

I  n + ^0   ( p !)

- 1

^{c 2} p I n + p ⁽ У )

TO

s

,

( p ^! ) ²

p = 0

где y = a2to0/4 . Выражение (5) дальше упростить не удаётся. Из (5) следует, что ОУМ аБГ-пучков больше n, так как все слагаемые рядов в (5) положительные. То есть с ростом параметра с растёт асимметрия аБГ-пучка и почти линейно растёт его ОУМ, как видно из рис. 2. Так как параметры α и c являются действительными положительными числами, то второе слагаемое в (5) может быть как целым, так и дробным положительным числом. Поэтому из (5) также следует, что аБГ-пучок нулевого порядка (n =0) может иметь любой ОУМ. Заметим также, что в (5) масштабные параметры пучка Бесселя α и Гауссова пучка ω0 входят в виде произведения, поэтому у разных аБГ-пучков, у которых αω0 = const, ОУМ будет одинаковым (при равных n и c).

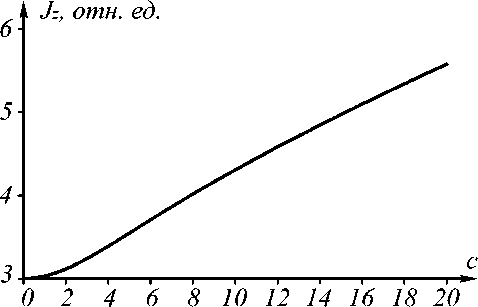
Рис. 2. Зависимость ОУМ от параметра асимметрии c при n = 3, to o = 10 X , a = 1/(10 X )

Для формирования аБГ-пучка был использован пространственный модулятор света SLM PLUTO-VIS (разрешение – 1920 × 1080 пикселов, размер пикселя – 8 мкм). Фаза и амплитуда пучка (1) кодировалась в виде только фазы и выводилась на этот модулятор [11]. На рис. 3 показаны распределения интенсивности аБГ-пучка, сформированные SLM на некотором расстоянии (а), и интенсивность в фокусе иммерсионного микрообъектива с высокой числовой апертурой (NA= 1,25) (б). Видно, что в случае, представленном на рис. 3, пучок при фокусировке поворачивается на 90 градусов и при этом сохраняет свою структуру с точностью до масштаба.

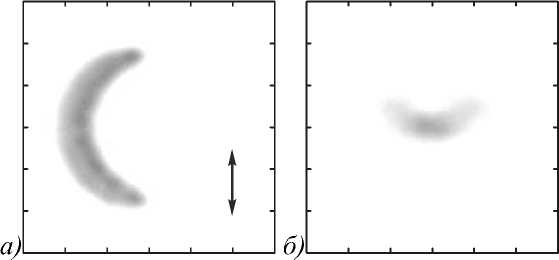
Рис. 3. Фокусировка асимметричного пучка Бесселя–Гаусса с помощью микрообъектива с высокой числовой апертурой (NA = 1,25). Полумесяц вытянут вдоль направления линейной поляризации освещающего пучка лазера (отмечено двунаправленной стрелочкой): а) распределение интенсивности в плоскости входного зрачка микрообъектива (шаг сетки равен 200 мкм);

б) распределение интенсивности в фокальной плоскости микрообъектива (шаг сетки равен 2 мкм)

• 2.    Эксперимент по передаче ОУМ микросферам полистирола с помощью асимметричных пучков Бесселя–Гаусса

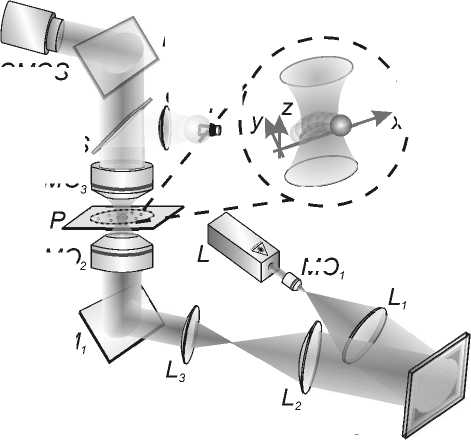
В этом параграфе мы экспериментально докажем, что с увеличением параметра асимметрии аБГ-пучка растёт ОУМ, и, значит, при прочих равных условиях большая часть ОУМ пучка должна передаваться микрочастице. Используемая оптическая схема показана на рис.4. Выходной пучок твердотельного лазера L (% = 532 нм, максимальная выходная мощность -1500 мВт) расширялся с помощью системы, состоящей из микрообъектива MO1 (16˟, NA=0,3) и линзы L1 (f1 =250 мм). Расширенный лазерный пучок направлялся на дисплей пространственного модулятора света SLM (PLUTO VIS, разрешение – 1920×1080 пикселов, размер пикселя – 8 мкм). Отражённый от модулятора модулированный лазерный пучок с помощью системы линз L2 (f2 = 350 мм) и L3 (f3 = 150 мм) направлялся во входное отверстие микрообъектива MO2 (60˟, NA = 0,85). Изображение плоскости манипулирования проецировалось на матрице CMOS камеры LOMO TC-1000 (разрешение – 1280×960 пикселов, размер пикселя 1,67 мкм) с помощью микрообъектива MO3 (16˟, NA=0,4). Для подсветки области захвата использовалась система, состоящая из конденсора C и освещающей лампы I, свет от которой вводился с использованием делителя пучка BS. Для манипулирования в эксперименте были использованы микросферы полистирола диаметром 5 мкм, которые находились на стеклянной пластинке P.

C

I

M 2

BS

MO

MO

M

SLM

Рис. 4. Экспериментальная схема установки для исследования передачи ОУМ микросферам полистирола с использованием асимметричных пучков Бесселя–Гаусса: L – твердотельный

CMOS

MO

лазер (λ = 532 нм, максимальная выходная мощность 1500 мВт), MO 1 – микрообъектив (8˟, NA = 0,3), L 1 , L 2 и L 3 – линзы с фокусными расстояниями (f 1 = 250 мм, f 2 = 350 мм, f 3 = 150 мм), SLM – пространственный модулятор света PLUTO VIS ( разрешение – 1920×1080 пикселов, размер пикселя – 8 мкм), MO 2 – микрообъектив (60˟, NA = 0,85), P – стеклянная пластинка со взвесью микросфер полистирола,MO 3 – микрообъектив (16˟, NA = 0,4), CMOS – видеокамера LOMO TC-1000 (разрешение – 1280×960 пикселов, размер пикселя – 1,67 мкм), C – конденсор, I – освещающая лампа, BS – делитель пучка

В зависимости от параметра c сформированного SLM (рис. 3) асимметричного пучка Бесселя–Гаусса в ходе экспериментов наблюдалось либо вращение микросфер полистирола вдоль сформированного светового кольца с асимметричным распределением интенсивности (при значениях c < 1), либо перемещение захваченных микросфер вдоль сформированной световой кривой в форме полумесяца (при значениях c ≥ 1). Типичные результаты экспериментов с использованием асимметричных пучков Бесселя–Гаусса с параметрами c1 = 0,3 и c2 = 3 и показаны на рис. 5 и 6 соответственно. В каждом из этих случаев значение параметра n равно 3. Как видно в экспериментах, представленных на рис.5, наблю-

Рис. 5. Распределение интенсивности в плоскости захвата (верхний левый кадр) и стадии движения трёх микросфер полистирола, захваченных с помощью асимметричного пучка Бесселя–Гаусса с параметрами n = 3, c = 0,3. Стрелочка показывает изменение положения одной из частиц

Во втором случае ( c 2 = 3) неподвижная микросфера полистирола, попав в область пучка, ускоряется и перемещается вдоль световой кривой (рис. 6), сформированной в плоскости захвата (средняя скорость перемещения равна 22,9 ± 1,0 мкм/с). Для формирования данных пучков были использованы выведенные на дисплей модулятора света фазовые функции, закодированные суперпиксельным методом [13].

Рис. 6. Распределение интенсивности в плоскости захвата

(верхний левый кадр) и стадии движения микросферы полистирола, захваченной с помощью асимметричного пучка

Бесселя–Гаусса с параметрами n = 3, c = 3. Стрелочка показывает изменение положения одной из частиц

Из уравнения (5) и рис. 2 видно, что на значение ОУМ влияние оказывает не только топологический заряд n сформированного асимметричного пучка Бесселя–Гаусса, но также и параметр c, отвечающий за асимметрию формируемого распределения интенсивности. Если считать, что мощность пучков с различными параметрами одинаковая, то отношение ОУМ двух асимметричных пучков Бесселя–Гаусса с различными параметрами c будет выражаться как (J    )/(J   ) . В табл. 1 приведены значения отно- z I c=c 1               z I c =1

шения ОУМ пучков с различными параметрами c к

ОУМ пучка с параметром c = 1,0. Для представленных пучков значение топологического заряда равно n =3.

Табл. 1. Рассчитанные по формуле (5) значения отношений

ОУМ асимметричных пучков Бесселя–Гаусса с параметрами c = 1,0; 1,5; 2,0; 2,5; 3,0 к ОУМ асимметричного пучка Бесселя–Гаусса с параметром c = 1,0. Топологический заряд пучков n = 3

с	1,0	1,5	2,0	2,5	3,0
( Ч >/< J- D	1,00	1,14	1,28	1,42	1,55

Для экспериментального подтверждения наличия данной зависимости были проведены эксперименты с асимметричными пучками Бесселя–Гаусса с параметрами c = 1,0; 1,5; 2,0; 2,5; 3,0, аналогичные показанным на рис. 5 и 6. Экспериментально измеренная эффективность формирования данных пучков совпадала в пределах погрешности используемого измерителя мощности. В табл. 2 приведены данные об экспериментально измеренных скоростях движения захваченных микросфер полистирола для каждого из сформированных пучков.

Табл. 2. Экспериментально измеренные значения скоростей движения полистироловых микросфер υ, захваченных с помощью асимметричных пучков Бесселя–Гаусса с одним и тем же топологическим зарядом n = 3, но с разными значениями параметра асимметрии c

с	и, мкм/c
1,0	13,6 ± 0,9
1,5	15,3 ± 1,8
2,0	17,5 ± 2,6
2,5	17,7 ± 2,8
3,0	19,0 ± 2,8

А в табл.3 – значения отношений величин скоростей движения полистироловых микросфер, приведённых в табл. 2.

Табл. 3. Экспериментально измеренные значения отношений величин скоростей движения полистироловых микросфер ( и |_с УС ^ с =1 ) , захваченных с помощью асимметричных пучков Бесселя–Гаусса с одним и тем же топологическим зарядом n = 3, но с разными значениями параметра асимметрии c

с	№)/( и | с = 1 )
1,0	1,0
1,5	1,1 ± 0,2
2,0	1,3 ± 0,2
2,5	1,3 ± 0,2
3,0	1,4 ± 0,2

На рис.7 представлена зависимость отношения экспериментально измеренных скоростей движения микросфер полистирола, захваченных с помощью асимметричных пучков Бесселя–Гаусса с различными значениями параметра c от значения данного параметра.

Видно, что с возрастанием значения c увеличивается средняя скорость движения захваченных микросфер. Скорость движения захваченных микросфер должна быть прямо пропорциональна переданному им ОУМ. В то же время формула (5) не учитывает такие факторы, как броуновское движение частиц, вязкость жидкости, градиентные и прочие силы, которые влияют на результаты измерения скорости микрочастиц.

Кроме того, экспериментально сформированные асимметричные пучки Бесселя–Гаусса формировались с помощью закодированных фазовых функций, которые не полностью учитывают амплитудную составляющую кодируемых комплексных распределений. Все эти факторы приводят к небольшим количественным отклонениям экспериментально измеренных отношений скоростей (табл.3) захваченных частиц (нормировка производилась относительно скорости движения микросфер, захваченных с помощью асимметричного пучка Бесселя-Гаусса с параметрами n = 3 и c = 1) от рассчитанных по формуле (5) отношений ОУМ (табл. 1) асимметричных пучков Бесселя–Гаусса, использованных при захвате (нормировка производилась относительно ОУМ асимметричного пучка Бесселя– Гаусса с параметрами n = 3 и c = 1). Наличие качественного соответствия эксперимента и численного расчёта очевидно из представленных результатов.

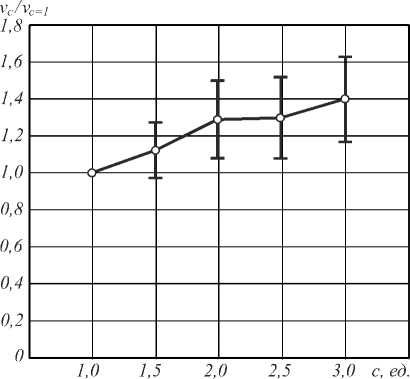
Рис. 7. Зависимость отношения экспериментально измеренных скоростей движения микросфер полистирола, захваченных с помощью асимметричных пучков Бесселя– Гаусса с различными значениями параметра c от значения данного параметра (n = 3)

Заключение

В работе экспериментально доказан близкий к линейному рост величины удельного орбитального углового момента лазерных асимметричных пучков Бесселя– Гаусса, предсказанный теоретически ранее в [1–4]. Для этого были проведены исследования по оптическому захвату, вращению и перемещению слабопоглощающих полистироловых шариков диаметром 5 мкм с помощью лазерных асимметричных пучков Бесселя–Гаусса с линейной поляризацией и длиной волны 532 нм, сформированных отражающим фазовым жидкокристаллическим микродисплеем и сфокусированных микрообъективом с числовой апертурой 0,85 в водный раствор этих микрочастиц. Эксперименты показали, что асимметричные пучки Бесселя-Гаусса с одинаковым топологическим зарядом (n =3) и одинаковой мощностью, но имеющие разную степень асимметрии по-разному вращают (перемещают) микрочастицы. С ростом параметра асимметрии (от с =1 до с =3) скорость движения микрочастиц по траектории пучка в поперечной плоскости почти линейно увеличи- лась в 1,4 раза. При этом орбитальный угловой момент пучка по теории должен увеличиться в 1,55 раза.

Работа выполнена при поддержке Министерства образования и науки РФ, гранта Президента РФ поддержки ведущих научных школ (НШ-9498.2016.9), и грантов РФФИ 14-29-07133, 15-07-01174, 15-3720723, 16-29-11698, и 15-47-02492