Оптическое деление частоты при распространении лазерного излучения в среде с насыщением поглощения и дисперсии

Задачи, связанные с изучением распространения мощного лазерного излучения в условиях резонанса, уже много лет привлекают к себе внимание исследователей (см., например, обзор [1] и ссылки в нём). Данные эффекты необходимо учитывать при оптическом зондировании атмосферы, стабилизации частоты лазеров, а также при оптимизации распространения лазерного сигнала в волоконно-оптических линиях связи и линиях задержки.

Под действием мощного лазерного излучения в условиях точного резонанса некоторые вещества начинают изменять свои оптические характеристики таким образом, что проявляется насыщение поглощения и дисперсии (показателя преломления). Эти эффекты вызывают возникновение наведённой дифракции лазерного пучка, приводящей к появлению резонансной самофокусировки [2]. Кроме того, в среде за счёт насыщения поглощения образуется канал наведённой прозрачности (эффект самопросветления среды), который способствует прохождению лазерного излучения на более значительные расстояния [3].

Большинство теоретических моделей нелинейной оптики строятся на основе описания отклика среды через нелинейную поляризацию и нелинейную восприимчивость среды на основе формализма матрицы плотности [4,5]. При рассмотрении распространения лазерного излучения в среде к этому описанию добавляется решение параболического волнового уравнения для поля. Очевидно, что тот же самый подход можно использовать для описания не только пространственных, но и временных зависимостей поля, так как они достаточно медленны и сравнимы с атомными временами релаксации. Подобные пространственно-временные численные модели достаточно удовлетворительно описывают проявления самофокусировки при распространении коротких импульсов (см., например, [6]).

Ранее нами [7] была подробно описана используемая численная модель и представлены результаты численного моделирования распространения модулированного лазерного сигнала в средах с насыщением поглощения и дисперсии. В настоящей работе основное внимание уделено нестационарной динамике дан- ной модели и анализу динамических режимов, при которых потенциально возможен переход к сложному многочастотному поведению и хаотическим колебаниям. Кроме того, весьма актуальной является задача анализа частотных изменений, возникающих при распространении модулированного лазерного сигнала в условиях насыщения поглощения и дисперсии, что важно в фазово-модуляционной спектроскопии насыщения, при формировании и делении оптических частот [5], а также при построении коммутаторов оптических сигналов [8].

Численная модель в рамках скалярной параксиальной оптики основывается на прямом решении уравнений Блоха (2,3), выводимых из уравнений для матрицы плотности и описывающих отклик среды совместно с параболическим волновым уравнением (1), которое описывает пространственно-временную эволюцию распространяющегося лазерного пучка (данная система из трёх уравнений в нелинейной оптике носит название системы уравнений Максвелла-Блоха):

d E 1 d E ^ , d ² 1 d .

— +--I + (—г +--) E = gP, dz c d t J dr2 r dr

^dD_ =_Y [D -1 + i (E- P - EP-)],(2)

ЭР г x I

— = -(Г+ iA) P - - Г DE ,(3)

о t2

где g – коэффициент поглощения, γ, Γ – скорости релаксации заселённости и поляризации, соответственно, D(z,ρ,φ,t) – разность заселённостей, нормированная на её величину в отсутствие насыщения, E(z,ρ,φ,t), P(z,ρ,φ,t) – медленно меняющиеся амплитуды электрического поля и поляризации, соответственно, Δ – отстройка несущей частоты от частоты атомного перехода. При решении уравнений (1-3) использовалось традиционное для исследований самовоздействия лазерного излучения приближение медленно меняющихся амплитуд (см., например, [9]). Это связано с тем, что в исходном состоянии среда является слабо нелинейной и слабо поглощающей, и амплитуды волн будут изменяться на малую величину при прохождении волной расстояния порядка длины волны, т.е. амплитуды волн будут медленно изменяющимися функциями эволюционной координаты z и времени t. Медленность амплитуд означает, что исследуется поведение огибающей модулированного лазерного сигнала, а не колебания вектора напряжённости электрического поля.

Поскольку рассматривается случай, когда несущая частота ω₀ равна частоте атомного перехода, то Δ = 0 в (3). Единица амплитуды поля соответствует уровню насыщения D = 0,5. Продольная координата z измеряется в единицах дифракционной длины L_d , представляющей собой характерное расстояние, на котором свободный пучок с данным радиусом и частотой удваивает своё сечение из-за дифракции. Поперечная координата r нормирована на начальный радиус пучка a , который во всех рассматриваемых случаях был взят равным 1.

Уравнения (1)-(3) решались при начальных условиях:

E ( z = 0, ρ , φ , t ) = E ⁰ ( ρ , φ , t ) ; E ( z , ρ , φ , t = 0) = 0;

D ( z , ρ , φ , t = 0) = 1; P ( z , ρ , φ , t = 0) = 0.

Для решения уравнений (1)-(3) нами была использована неявная разностная схема второго порядка, основанная на разложении поля по поперечной координате по модам Гаусса-Лагерра, подробно описанная в [7]. Были рассмотрены пучки, симметричные относительно оси распространения с начальным гауссовым профилем. Частота пучка на входе в среду гармонически модулирована по времени, ω = ω 0 + ω 1 sin Ω t , где ω 0 – несущая лазерная частота, ω 1 – амплитуда модуляции частоты, Ω – частота модуляции. В этом случае комплексная амплитуда входного поля представляется в виде:

ρ ² ω

E (0, ρ , φ , t ) = E ₀ exp( - ) exp[ i ¹ cos( Ω t )]. (4) 2 a ² Ω

В случае точного резонанса (Δ =0 ) частота модулированного поля осциллирует симметрично по отношению к несущей. Время и частота нормированы на времена релаксации заселённостей γ и поляризации Γ . Для упрощения были взяты γ = Γ = 1.

Были рассмотрены различные модуляционные режимы, отличающиеся значениями Ω и ω1, а также различные режимы насыщения, зависящие от интенсивности лазерного излучения.

Исследуемыми физическими параметрами, представленными на рис. 1, являются интенсивность пучка на выходе из среды I ( z , r , t , ω), выражающаяся как квадрат модуля комплексной амплитуды поля Е : I ( z , ρ, φ, t , ω)=| E ( z , ρ, φ, t , ω)|² , и размер пятна w ( t ) , определяемый как второй момент поперечного распределения нормированной интенсивности:

2π ∞ w2(t) = J dфJP3dp|E(Z, p,ф, t)|2 x

2π ∞ x j J dфJp dp|E(Z, p, ф,t)|2

I 0     0

В соответствии с правилами исследования нелинейно-динамических систем, для анализа нестационарного поведения лазерного сигнала были проанализированы фазовые диаграммы на плоскости «поляризация среды P – разность заселённостей D », иллюстрирующие динамику отклика среды на воздействующее излучение, а также спектры мощности, рассчитанные по реализации интенсивности на оси пучка на выходе из среды (рис. 2).

Рассматривался режим слабой, низкочастотной модуляции, (Ω = 0,25), когда спонтанные эффекты отклика среды пренебрежимо малы, при этом амплитуда частотной модуляции была взята равной ω 1 =1.

В этом случае можно предположить наличие существенной амплитудной модуляции выходной интенсивности из-за постоянного изменения поглощения.

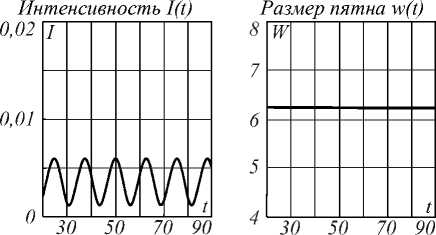
Были исследованы режимы слабого насыщения, вызываемого полем невысокой интенсивности ( E 0 = 0,1) (рис. 1 а ), когда эффекты резонансного са-мовоздействия пучка не возникают; среднего насыщения ( Е 0 =5) (рис.1 б ), когда начинается проявление эффектов резонансного самовоздействия; сильного насыщения ( Е 0 = 10, Е 0 = 20) (рис. 1 в, г ), когда эффекты резонансного самовоздействия весьма значительны; и сверхсильного насыщения ( Е ₀ = 100) (рис. 1 д ), когда происходит выравнивание заселённостей уровней и эффекты резонансного самовоз-действия уже отсутствуют.

Распространяясь в резонансной поглощающей среде, пучок постепенно приобретает модуляцию интенсивности, которая вызывается разницей поглощения на различных частотах. Этот эффект возникает даже при низких интенсивностях и низких частотах модуляции и исчезает при сверхсильном насыщении, что легко объясняется выравниванием заселённостей уровней и, как следствие – равенством поглощения на разных частотах. Это, в свою очередь, приводит к исчезновению эффектов наведённой рефракции и режиму самоканалирования в среде (рис. 1 д ), когда поведение пучка напоминает случай слабого поля (рис. 1 а ).

В линейном режиме (рис. 1 a, E 0 = 0,1) модуляция выходной интенсивности близка к гармонической, её частота равна удвоенной частоте модуляции. Это следует из того факта, что симметричные сдвиги лазерной частоты в обе стороны от резонанса вызывают одинаковые изменения линейного поглощения.

Размер пятна в этом случае не зависит от частотной модуляции, так как отсутствует навёденная линза. На фазовом портрете поляризации среды P и разности заселённостей D , а также на спектре мощности интенсивности выходного сигнала (рис. 2 а ) можно наблюдать режим периодических колебаний с частотой модуляции 1/ T и удвоение периода 2 T .

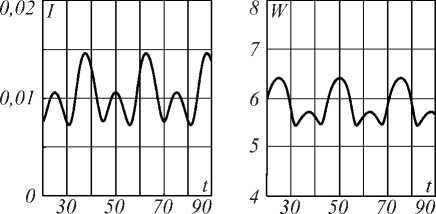
В режиме насыщения (рис. 1б, E0 = 5) полупериоды модуляции становятся неравными, так как наведённая линза является положительной при час- тоте выше атомного перехода и отрицательной при частоте ниже перехода. Таким образом, увеличение интенсивности из-за слабого поглощения на частоте ниже резонанса сглаживается дефокусировкой.

а)

б)

в)

г)

д)

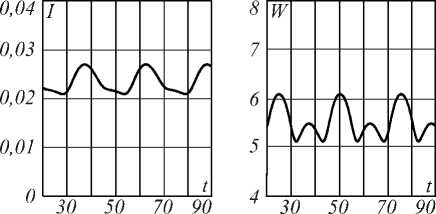
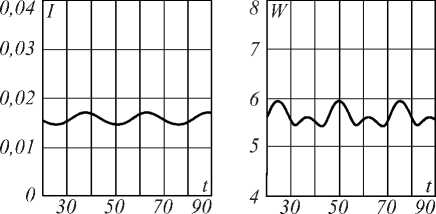
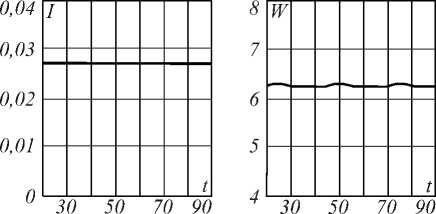
Рис. 1. Зависимость от времени выходной интенсивности I(t) (слева) и размера пятна w(t) (справа) при E₀=0,1 (а); E 0 =5 (б); E 0 =10 (в); E 0 =20 (г); E 0 =100 (д)

г)

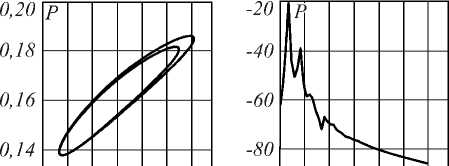
0,12 \ I I I I I 1^1 _ioq\ I I I I I lyl 0,08   0,12   0,16       0    4    8   12

д)

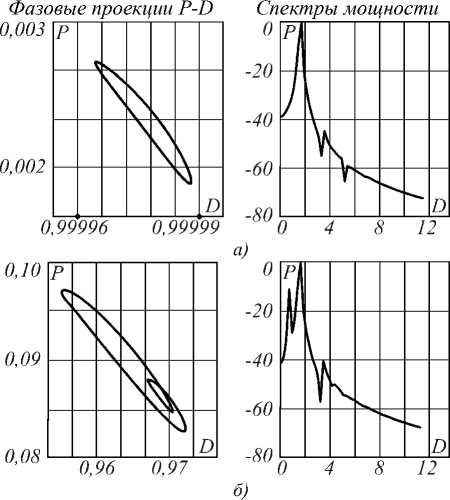
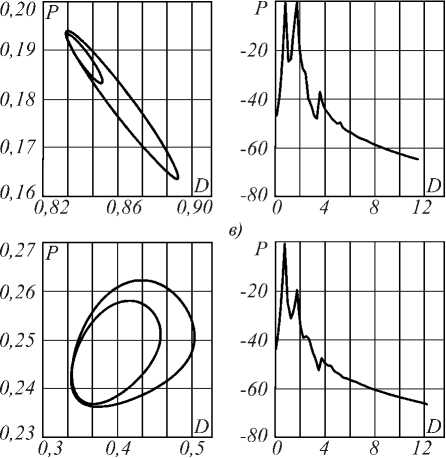
Рис. 2. Проекции фазового пространства системы на плоскость «поляризация среды P – разность заселённостей D» (слева) и спектры мощности, рассчитанные по реализации интенсивности на оси пучка на выходе из среды (справа) при E0=0,1 (а); E0=3 (б);

E 0 =5 (в); E 0 =10 (г); E 0 =20 (д)

Прослеживается явная зависимость изменений интенсивности и поведения размера пятна – возни- кает периодическая пульсация пучка, вызванная фокусировкой и дефокусировкой на различных частотах.

При этом возникает субгармоника, хорошо заметная и на фазовом портрете и на спектре мощности (рис. 2 б ), что свидетельствует о постепенно возрастающем влиянии эффектов резонансного само-воздействия, вызывающих понижение частоты наведённой амплитудной модуляции.

В фокусирующей области пики интенсивности становятся больше. Размер пятна демонстрирует пульсации, вызванные резонансной фокусировкой и дефокусировкой, причём в центре каждой фокусирующей области заметно увеличение после спада (рис. 1 б ).

С увеличением интенсивности поля происходит подавление первой гармоники и рост амплитуды субгармоники, что объясняется постепенным уменьшением разности заселённостей D и нарастающим влиянием эффекта дефокусировки на частотах ниже резонансной. Колебания на основной частоте постепенно сглаживаются и при Е 0 =20 частота колебаний уменьшается вдвое, при этом на спектре мощности наблюдается только субгармоника 2 T (рис. 2 д ).

Дальнейшее увеличение интенсивности приложенного поля приводит к выравниванию заселённостей уровней и просветлению среды, когда поглощение столь незначительно, что становится практически одинаковым при любой частоте. Как следствие этого эффекта, мы наблюдаем отсутствие наведенной амплитудной модуляции интенсивности (рис. 1 д ) и режим колебаний периода T .

Таким образом, проанализировав пространственные и частотные характеристики лазерного пучка в условиях резонансного самовоздействия, можно сделать вывод, что нелинейно-оптическая двухуровневая среда при достижении определённой мощности модулированного излучения, распространяющегося в условиях резонанса, может выполнять роль оптического делителя частоты, что является весьма полезным эффектом с целью его практического применения в методике измерения больших интервалов оптических частот [5], заменяя кристаллы с керровской нелинейностью и сложные схемы делителей частоты. В качестве такой нелинейнооптической среды можно использовать, например, пары натрия, где эффекты резонансного самовоз-действия весьма значительны и достаточно контролируемы (см., например, эксперименты [3] или [10]).

Кроме того, детальный анализ условий возникновения и исчезновения амплитудной модуляции распространяющегося лазерного пучка может оказать существенное влияние на более точное вычисление и идентификацию сигнала ошибки, возникающего при регистрации субдопплеровских спектров в фазово-модуляционной спектроскопии насыщения и при использовании метода переноса спектра модуляции [5], используемого при стабилизации частоты лазеров.

Авторы благодарят к.ф.-м.н. Мантурова А.О. за полезные консультации и обсуждение результатов работы.