Оптическое выделение контуров пропускающими структурами металл-диэлектрик-металл

Реализации полностью оптических преобразований оптических сигналов и изображений уделяется значительное внимание, поскольку это открывает возможности к осуществлению сверхбыстрых аналоговых потоковых преобразований [1, 2]. Переход от традиционных оптических систем на основе громоздких систем линз и фильтров к миниатюрным системам, не требующим выполнения преобразования Фурье, может быть осуществлён на основе резонансных оптических структур.

Большой интерес вызывает выполнение операций оптического дифференцирования и интегрирования различных порядков, преобразования Лапласа [3 –6]. Точное выполнение этих операций требует подобия зависимости коэффициента отражения от пространственной или временной частоты этих структур передаточным функциям соответствующих операторов. Так, были получены аппроксимации резонансных спектров отражения (пропускания) дифракционных [3, 7– 10], слоистых плазмонных [11, 12] и волноводных [13] структур, границ раздела диэлектрических сред [14– 18], характеризуемые различными спектральными диапазонами их применимости, а также различной шириной резонансов.

Кроме того, для выполнения полностью оптических вычислений были предложены трёхмерные оптические структуры [1, 19–21] на основе метаповерхностей в виде массива нанорезонаторов. Следует отметить, что изготовление резонансных слоистых структур существенно менее трудоёмко по сравнению с процессами изготовления метаповерхностей и дифракционных двухмерных и трёхмерных структур.

Подходы к оптическому дифференцированию на основе слоистых структур были теоретически исследованы и экспериментально продемонстрированы на примере выделения контуров на изображениях амплитудных и фазовых образцов для p-поляризованных пучков. Так, описывалось применение резонансов в спектрах нарушенного полного внутреннего отражения тонких металлических плёнок в конфигурации Кречмана, ассоциируемые с возбуждением плазмонной моды [11, 12], а также резонансного уменьшения отражения от грани стеклянной призмы при падении пучка под углом Брюстера

[15–18]. Теоретически, операция дифференцирования требует достижения строгого нуля на центральной частоте, что осуществляется в экспериментах на основе эффекта Брюстера. Несмотря на то, что плазмонные структуры, описанные в [11], не были оптимизированы для достижения строгого нуля, для них продемонстрировано эффективное выделение контуров с подавлением фона. Таким образом, структуры, передаточные функции которых отличны от идеальных, могут применяться в областях оптической информатики, не требующих точной обработки информации.

Значительное количество работ было посвящено исследованию оптических характеристик отражающих структур типа металл–диэлектрик–металл (МДМ), один из слоёв металла которой является оптически толстым. Возбуждение собственных мод МДМ-структур приводит к резонансному усилению поглощения света и появлению резонансов в спектрах отражения [22–27]. Применение отражающих структур для обработки изображений требует разделения падающего и отражённого пучков, что усложняет оптическую схему.

МДМ-структура, в которой слои металла достаточно тонкие для регистрации спектров пропускания, позволяет использовать более простую оптическую схему. В этом случае МДМ-структура рассматривается как резонатор Фабри–Перо с поглощающими зеркалами [28]. При резонансных условиях интерференция многократно переотражённых лучей в диэлектрическом слое приводит к усилению поля их интерференции. Теоретическое и экспериментальное исследования спектров пропускания показали, что возбуждение в структуре мод Фабри–Перо приводит к появлению в спектрах пропускания областей резонансного увеличения пропускания [28]. Резонансные области разделяются областями минимального пропускания. Однако возможность достижения строгого нуля в минимумах пропускания таких структур выяснена не была.

На основе исследований резонансного отклика структур МДМ, работающих на пропускание, можно предположить, что операция оптического дифференцирования не может быть точно реализована. Резонансный профиль в спектрах таких структур потенциально может быть использован для осуществления оптического подавления интенсивности направленного излучения источника относительно интенсивности рассеянных на объекте волн.

В настоящей работе впервые исследуется возможность применения резонансных пропускающих слоистых структур МДМ на стеклянной подложке на основе слоёв алюминия (Al), разделённых слоем диоксида кремния (SiO2), для полностью оптического выделения контуров на изображениях оптических структур. Из результатов работы следует, что резонансные структуры МДМ могут эффективно приме- няться для неточной обработки оптических сигналов в проходящем свете.

1.    Описание структуры МДМ

Для экспериментальной демонстрации была изготовлена структура вида металл–диэлектрик–металл, а именно последовательно нанесённые на подложку из стекла K8 слой Al толщиной 20 нм, слой SiO 2 толщиной 4022 нм и слой Al толщиной 20 нм. Изготовление слоёв проводилось на установке магнетронного нанесения (Изовак) в автоматическом режиме в течение времени, рассчитанного на основе средней скорости напыления каждого материала в отдельности, при давлении не более 3×10 ^–3 Па [28].

Спектры пропускания были получены измерениями на спектрофотометре Photon RT (ЕссентОптикс) в воздухе и представлены на рис. 1 как функции угла падения θ волны на структуру к её нормали и длины волны луча. Теоретическое моделирование спектров пропускания структуры Al/SiO 2 /Al показало, что возникновение максимумов пропускания величиной более 1,5% на фоне минимумов величиной менее 0,1 % происходит благодаря резонансному возбуждению мод Фабри–Перо различных порядков. Возбуждение мод, характеризуемое резонансным усилением пропускания, происходит при больших углах падения для меньших длин волн. Как видно на рис. 1, кривые возбуждения мод располагаются под небольшим углом к оси угла падения, что предполагает малую ширину резонансов в частотных спектрах и большую ширину – в пространственных. С увеличением угла падения наклон кривых к оси угла падения увеличивается, что предполагает уменьшение угловой ширины резонанса, а также углового расстояния между ближними резонансами.

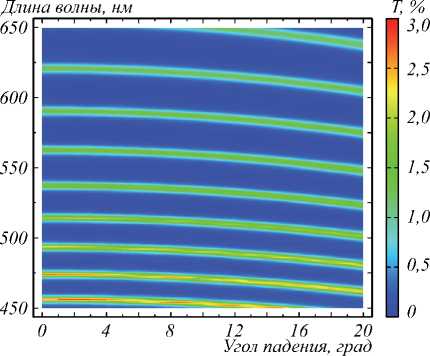
Рис. 1. Распределение измеренной пропускающей способности T структуры Al/SiO 2 /Al для широкого диапазона длин волн

Для демонстрации зависимости ширины резонанса и расстояния между резонансами от угла падения угловые спектры пропускающей способности структуры МДМ для ряда значений длин волн приводятся на рис. 2. Определим контраст структуры как К (θ, |θmax – θ|)= T (θmax) / T(θ), где θmax – значение угла падения волны на структуру к её нормали, для которого наблюдается резонансный максимум, при этом значение θmax – ближайшее к значению угла падения коллимированного пучка θ. Отметим, что в соответствии с измеренными данными, для нормального падения пучка контраст возрастает с удалением положения резонансного максимума пропускания θmax от нормального падения от К(0, 8º)=2,5 при 561 нм до К (0, 17º) = 17 при 555 нм.

Выделение контуров на изображениях оптических объектов производится за счет фильтрации углового спектра, в результате которой интенсивность фонового излучения становится ниже интенсивности рассеянного на краях излучения.

В случае использования эффекта Брюстера (угол падения пучка на границу раздела двух диэлектрических сред равен углу Брюстера θ Br ) оценки значений контраста коэффициента отражения структуры, необходимого для эффективного выделения контуров изображения объекта относительно падающего излучения, составляют, например, К (θ Br , 1º)= 100 и К (θ Br , 3º)= 1000 [15– 18]. Таким образом, значения контраста, достигаемые в изготовленной структуре Al/SiO 2 /Al для углов вблизи нормального падения, недостаточны для использования данного образца для задачи выделения контуров при нормальном падении. Теоретические исследования структур на основе серебра (Ag) [29] показали, что в случае нормального падения контраст может быть увеличен на порядок по сравнению со значениями структур на основе Al. Однако наши эксперименты продемонстрировали значительное ухудшение контраста при окислении Ag, возникающем при изготовлении структур или при нахождении образцов структур в атмосфере.

В соответствии с рис. 2 достижение приемлемых уровней контраста для меньших отклонений положения максимума пропускания от угла падения пучка возможно для больших углов падения пучка. В случае θ = 48,3º контраст К (48,3º, 3º) = 7 при 561 нм до К (48,3º, 5,1º) = 11 при 555 нм.

т, %

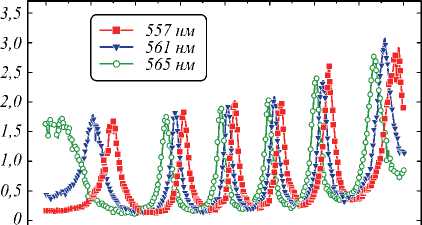
О 10   20   3 0   40   5 0   6 0   70   80

Угол падения, град

Рис. 2. Измеренные угловые спектры пропускающей способности структуры Al/SiO 2 /Al для значений длин волн в диапазоне 557–565 нм

2.    Преобразование Гауссовых пучков

Оптическая система схематично изображена на рис. 3. В качестве источника света был использован перестраиваемый лазер EKSPLA NT242. Регулировка мощности выходного пучка осуществлялась фильтром нейтральной оптической плотности ND. Поляризатор P настроен на пропускание p-поляризованного излучения, при этом колебания электрического вектора происходят в плоскости падения луча. Расширение и коллимация пучка осуществлялись коллиматором, состоящим из микрообъектива М и линзы L 1 , а также пинхола (апертуры) А , расположенного в фокальной плоскости микрообъектива и линзы.

РА   S

ND М Li L2 CCD

Рис. 3. Оптическая схема для демонстрации углового спектра пропускания изготовленной резонансной структуры S

Сколлимированный пучок фокусируется линзой L 2 . На расстоянии, большем, чем фокусное расстояние линзы L 2 , располагается ПЗС-матрица CCD. Между линзой и ПЗС-матрицей помещается образец структуры МДМ S , установленный перпендикулярно оптической оси. Такая оптическая схема позволяет осуществлять регистрацию угловых спектров пропускания образца S . При этом распределение интенсивности I ( x , y ), зарегистрированное ПЗС-матрицей в декартовой системе координат, в полярной системе координат соответствует спектральному распределению I (θ, ϕ) = I ( x , y ), где ϕ =atan( y / x ) и θ = atan ( r / d ), где r – радиус зарегистрированного кольца, d – расстояние от фокальной плоскости линзы L 2 до ПЗС-матрицы, как показано на рис. 4.

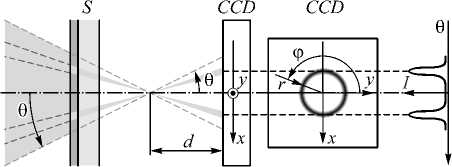
Рис. 4. Оптическая схема преобразования пучка фильтрацией углового спектра образцом S в случае нормального падения

На рис. 5 приведены экспериментально полученные изображения р-поляризованных Гауссовых пучков после прохождения структуры для ряда значений длин волн. Исследуемая структура не производит точной операции дифференцирования из-за невозможности достижения строгого нуля при нормальном падении. Кроме того, в [28] было теоретически показано, что резонансные максимумы в спектрах вблизи нормального падения аппроксимируются функциями

Лоренца, тогда как подобной зависимости для резонансных минимумов получено не было. Из рис. 5 видно, что угловые спектры пучка, прошедшего структуру, обладают центральной симметрией с хорошей равномерностью интенсивности по ϕ, что согласуется с теоретическими выводами в [28] о пренебрежимо малом влиянии поляризации на положение резонанса θ res при падении пучка, близком к нормальному. Кольца в изображениях преобразованных пучков характеризуются угловой шириной, соответствующей нескольким градусам, как следует из распределений угловых спектров, представленных на рис. 1. Контраст преобразованного структурой Гауссова пучка как отношение значений интенсивности на кольце к значениям интенсивности в центре принимает значения в диапазоне 1,5–2,5.

Рис. 5. Примеры экспериментальных изображений углового распределения пучков в случае нормального падения для отдельных значений длин волн

Для качественной демонстрации принципиальной возможности осуществления оптической операции выделения контуров на изображениях с использованием структур МДМ мы провели эксперимент с образцом Al/ SiO 2 /Al, расположенным под углом к оптической оси α. При этом симметрия преобразования пучка по угловому спектру нарушается, как схематично изображено на рис. 6. На рис. 7 приведены результаты экспериментальных измерений пространственных спектров пучков, прошедших структуру в случае α = 40º, для длин волн 553 нм, 556 нм и 559 нм. Как видно из рисунка, спектральный состав излучения представляется в виде концентрических дуг, положение которых сдвигается к центру с увеличением длины волны. В случае наклонного положения ПЗС-матрицы параллельно структуре S регистрируются концентрические окружности. Пересечение вертикальных линий на рис. 7 обозначает положение лучей, распространяющихся вдоль оптической оси.

Как видно на рис. 7, угловое расстояние от направления нормального падения до направления максимумов пропускания для волн рассеянного излучения, распространяющихся в горизонтальной плоскости, меньше, чем для волн, распространяющихся в вертикальной плоскости. Это является причиной за- висимости эффективности выделения контуров на основе подсвечивания рассеянного излучения от преимущественного направления рассеяния, как будет показано ниже.

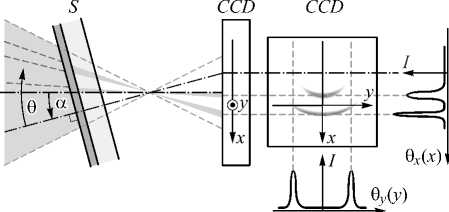
Рис. 6. Оптическая схема преобразования пучка фильтрацией углового спектра образцом S в случае наклонного падения

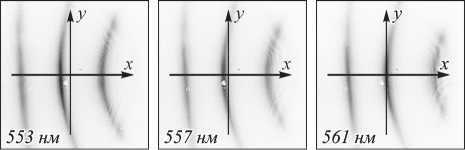
Рис. 7. Экспериментальные изображения углового распределения пучков в случае наклонного падения для отдельных значений длин волн

3.    Экспериментальная демонстрация выделения контуров изображения фазового объекта

Для демонстрации оптического выделения контуров схема, представленная на рис. 3, перестроена, как показано на рис. 8. Пучок, коллимированный линзой L 1 , освещает объект О . На расстоянии от f 2 до 2 f 2 от объекта О размещается линза L 2 , где f 2 – фокусное расстояние линзы L 2 . На расстоянии, большем f 2 , от линзы L 2 помещается ПЗС-матрица CCD для регистрации изображения объекта О . Структура для оптического преобразования размещается на любом расстоянии между объектом О и линзой L 2 . В качестве фазового объекта используется маска в прозрачной плёнке полимера с показателем преломления 1,46 на 532 нм и толщиной 550 нм на стеклянной подложке.

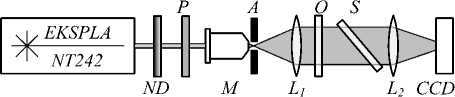
Рис. 8. Оптическая схема выделения контуров на изображении объекта O в случае наклонного падения освещающего пучка на резонансную структуру S

Рассмотрим формирование оригинального изображения объекта без резонансной структуры МДМ. Маска состоит из перекрещенных полос шириной 100 мкм. Пучок, прошедший через подложку и полимер, приобретает набег фазы по сравнению с пучком, прошедшим только подложку. На матрице CCD изменение фазы не регистрируется. Поглощение полимера мало, показатели преломления полимера и стек- лянной подложки имеют близкие значения, поэтому интенсивность изображения объекта сопоставима для областей, покрытых полимером, и без покрытия. Вдали от краев маски, где происходит рассеяние падающей волны, направление пучка не меняется. В окрестности краев маски происходит скачок фазы и возникает прошедшее и отражённое рассеянное излучение, распространяющееся в прямом и обратном направлениях соответственно. Это приводит к уменьшению интенсивности краёв объекта на оригинальном изображении, как видно на рис. 9а.

В краевых областях в результате дифракции на неоднородностях объекта наблюдается модуляция интенсивности, как можно увидеть на рис. 9 а . При смещении объекта вдоль оптической оси или его отклонении от плоскости изображения амплитуда модуляции возрастает с размытием изображения объекта. Появляющиеся в результате дифракции вторичные контуры изотропно огибают границы объекта. Для минимизации влияния дифракции на изображение, плоскости линз, объекта и ПЗС-матрицы располагались перпендикулярно оптической оси по отраженному пучку. Настройка положения ПЗС-матрицы вдоль оптической оси осуществлялась для достижения максимального контраста изображения.

Для проверки осуществимости выделения контуров на основе резонансного пропускания структура Al/SiO 2 /Al устанавливалась под углом α к оптической оси. Сканированием длины волны перестраиваемого лазера изменялись резонансные характеристики структуры и, соответственно, режим преобразования изображения.

В случае установки структуры в плоскости, перпендикулярной оптической оси (α = 0°), приемлемые результаты, демонстрирующие выделение контуров на изображениях, не были получены. При установке структуры под углом α около 40° типичные изображения, полученные в результате преобразования, представлены на рис. 9 б и 9 в .

Рис. 9. Изображения фазового образца: оригинальное (длина волны 561 нм) (а) и преобразованное с использованием структуры МДМ, установленной под наклоном α = 40° к оптической оси, при длинах волн 561 нм (б) и 557 нм (в)

При длине волны 561 нм, согласно рис. 7б, область максимума пропускания соответствует направлению лучей, распространяющихся вдоль оптической оси. В этом случае пропускание излучения, рассеянного на краях объекта, сопоставимо с пропусканием лучей, распространяющихся вдоль оптической оси. Это приводит к регистрации преобразованного изображения (см. рис. 9б), которое отличается от ориги- нального большим отклонением яркости фона от яркости краёв.

При уменьшении длины волны на 4 нм до 557 нм согласно рис. 7 в направление лучей, рассеянных на краях объекта, соответствует максимуму пропускания в спектре. При этом пропускание падающего пучка принимает значения, близкие к минимальным. Это приводит к регистрации преобразованного изображения (см. рис. 9 в ), на темном фоне которого наблюдаются вертикальные яркие линии, соответствующие вертикальным краям маски и градиентам неоднородности объекта, направленным в горизонтальной плоскости, которая характеризуется меньшим расстоянием между резонансными максимумами. Линии, соответствующие горизонтальным краям маски, не проявляются, поскольку градиент неоднородности объекта для них направлен в вертикальной плоскости, характеризуемой большим расстоянием между резонансными максимумами. В отличие от дифракционного выделения контуров, в случае использования резонансной структуры подсветки горизонтальных краёв маски, для которых градиент неоднородности направлен в вертикальной плоскости, не происходит. Это объясняется большей угловой шириной между резонансными максимумами в вертикальном направлении, как схематично показано на рис. 6.

Как показано на рис. 9 б и 9 в , изменение длины волны света на несколько нанометров приводит к качественному изменению характера представления контуров и фона за счет изменения соотношения интенсивностей изображений фона и краёв объекта. Такая сильная зависимость выделения контуров от длины волны не характерна для дифракционных эффектов. Таким образом, экспериментально наблюдаемые эффекты выделения контуров ассоциируются с оптической фильтрацией, выполняемой резонансными структурами МДМ.

Заключение

Проведенное экспериментальное исследование впервые демонстрирует принципиальную возможность применения резонансных структур МДМ, работающих на пропускание, для оптической обработки изображений. Проведённый анализ пространственных спектров пропускания МДМ структур на основе слоя кварца, заключённого между слоями алюминия, показал наличие достаточно узких и высоких резонансов в области наклонного падения. Использование резонансных свойств структур МДМ позволило осуществить эффективное выполнение пространственной операции выделения контуров на изображениях объектов в случае наклонного падения. В отличие от эффектов, вызванных дифракцией, выделение контуров изображения на основе структур МДМ осуществляется для определённых длин волн в узких диапазонах угла падения освещающего пучка.

Планируется провести изучение возможности выделения контуров для случая нормального падения в следующих экспериментальных исследованиях. Полученные результаты могут быть использованы для создания компактных систем сверхбыстрых аналоговых вычислений и обработки изображений реального времени, для расширения возможностей существующих и для создания новых оптических устройств, в том числе систем на чипе.

Работа выполнена при поддержке Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (соглашение № 007-ГЗ/Ч3363/26) в части постановки задачи и Российского фонда фундаментальных исследований (проекты 18-2920006 и 18-07-00613) в частях теоретического, численного и экспериментального исследований.