Оптика в моделировании водной поверхности в реальном времени

Для того чтобы добиться в компьютерной графике фотореалистичности, нужны два элемента: точное представление свойств водной поверхности и хорошее физическое описание эффектов освещения на сцене. В число этих эффектов входят отражение света, преломление света и каустика.

В зависимости от качества поверхности изображения делят на:

• •    зеркальные отражения. Чаще всего используются для гладких поверхностей;

• •    диффузные отражения. Они применимы для шершавых поверхностей;

• •    смешанные отражения - это совокупность зеркального и диффузного отражений.

Интенсивность отражённого света, которая характеризуется коэффициентом отражения, зависит от показателей поляризации падающих лучей на поверхность и от угла падения, а также зависит от того, как соотносятся значения преломления n ₂ и n соответственно 2-ой и 1-ой сред [1, с.8]. Для той среды, которая является отражающей (она же диэлектрик) зависимость показывают уравнения Френеля. Из этих уравнений следует, что коэффициент отражения не зависит от поляризации падающих лучей при падении света на нормаль к поверхности. В таком случае этот коэффициент будет равен следующему выражению (формула 1).

(п^п^ («2-14?

Зеркальное отражение, которое мы видим на блестящих поверхностях, является результатом полного отражения света от поверхности (или почти полного отражения), в определенной области рядом с углом отражения.

К точечному источнику света \

Направление отражённого света

К точке наблюдения

Рис 1 - Схема зеркального отражения от поверхности

На рис. 1 для точки на освещенной поверхности показано направление зеркального отражения. Угол падения света равен углу зеркального отражения, при этом углы отмеряются в противоположных направлениях от вектора нормали N, равному единице, к поверхности. На представленном рисунке: вектор R – это единичный вектор, который направлен в сторону идеального зеркального отражения, L – единичный вектор, который направлен к точечному источнику света, V – единичный вектор, направленный к наблюдателю. Угол α – это угол наблюдения относительно направления спектрального отражения R. В случае идеального отражения падающий свет отражается только в направлении зеркального отражения, и он становится видимым, если векторы R и V совпадут.

Эмпирическая модель расчета диапазона зеркального отражения разработана Буи Туонгом Фонгом и называется моделью зеркального отражения Фонга [2].

Диффузное отражение от какой-либо поверхности можно смоделировать, сделав предположение, что падающий свет рассеивается с одинаковой интенсивностью во все направления. Рассеяние света не зависит от направления наблюдения. Такие поверхности называются идеальными диффузными отражателями. В некоторых источниках их называют Ламбертовскими отражателями, так как световая энергия, отраженная от любой точки поверхности подчиняется закону косинусов Ламберта. Этот закон показывает, что для поверхностей, подчиняющихся этому закону, яркость во всех направлениях одинакова и сила света элемента поверхности изменяется пропорционально косинусу угла между нормалью к поверхности и данным направлением.

Для моделирования водной поверхности было применено смешанное отражение для достижения высокой реалистичности. В случае смешанного отражения света часть света отражается диффузно, а часть света – зеркально. Та же самая поверхность в зависимости от показателей может быть различной: для света, который мы видим, она будет диффузно-отражающей, матовой, но при этом также гладкой и зеркально-отражающей поверхностью.

Также для водной поверхности необходимо смоделировать эффект преломления. Он так или иначе связан с пропусканием. Преломление – это изменение направления движения света при пересечении границы двух сред. У каждого материала различные показатели преломления. Эти показатели и являются коэффициентами преломления.

Если коэффициент преломления равен нулю, то это значит, что объект будет невидим на экране. У него самый высокий показатель прозрачности, так как поток лучей не искривляется, и среды имеют равные показатели плотности. Преломление происходит из-за разных показателей плотностей сред. Когда свет проходит сквозь более плотную среду, он движется медленнее. Стоит помнить, что вода – среда оптически более плотная, чем воздух. Следовательно, согласно закону преломления света, угол преломления в рассматриваемом случае будет всегда меньше угла падения.

При моделировании водной поверхности также необходимо рассмотреть понятие дифракции волн и уравнения Френеля для отражения света.

Дифракция волн – это явление, которое показывает себя, как отклонение от законов геометрической оптики при распространении волн. Она представляет собой универсальное волновое явление. Характеризуется одинаковыми законами при наблюдении любых волновых полей различной природы.

Уравнения Френеля (часто их называют коэффициентами) – это коэффициенты, которые определяют соотношение показатлей преломленной энергии и показателей отраженной энергии на границе двух сред с разными показателями преломления. Эти коэффициенты широко используются в компьютерной графике при моделировании различных отражающих поверхностей (вода, стекло, металл).

Если смотреть в воду под большим углом, находясь сверху, то можно увидеть дно, а если под достаточно малым углом по касательной, то дна уже будет не видно, так как водная поверхность будет отражать небо, как зеркальная поверхность. В компьютерной графике, при моделировании подобных эффектов, переход от видимого преломления к отражению задается коэффициентом Френеля, который напрямую зависит от материала среды (вода, стекло, и др.).

Математическая формула зависит от угла падения, и она для вычисления количества отраженной энергии будет выглядеть как в формуле frenelW =

17 • cos(e)-Vl- (q sinCe))2

31 ' ^cos (9) + _л,' 1 — Gj- sin (9) J ²

где η – это показатель отношения коэффициентов преломления сред.

Так как обычно на практике имеется только косинус угла падения, который рассчитывается, как скалярное произведение вектора направления взгляда на нормаль в данной точке, то данная формула Френеля выражается через косинус угла, но так как она получается довольно громоздкой и сложной для вычисления, поэтому чаще всего используют более простые формулы (3) и (4).

Fl(cos 0) =

1+ cos 9^ '

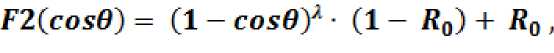
где степень X подбирается экспериментально, ^ 0 – коэффициент отражения при нормально падении (перпендикулярно плоскости).

Следовательно, так можно получить коэффициент, который определяет долю отраженной энергии.

В различных графических пакетах фактор Френеля для отражения ограничен диапазоном. Например, в пакете Blender ограничение задано значениями от 0 до 5. Этот параметр задает интенсивность проявления эффекта Френеля и чем больше этот фактор, тем сильнее влияние эффекта Френеля. При значении 0 эффект Френеля не проявляется.

Таким образом, мы рассмотрели подход к созданию оптических эффектов водной поверхности, которые можно применять для отрисовки графики в реальном времени.