Optimal choice of design parameters of the umbrella-type antenna spoke to reach maximal bending stiffness

Introduction. Large deployable parabolic antennas are widely used in satellite communication systems. Umbrella-type constructions with radial spokes-ribs connected at one end to the base are the most widespread among such systems (fig. 1).

Spokes are the main supporting elements of an umbrella-type antenna. They must have bending stiffness sufficient to open the antenna and to tense the netting both during the orbital operation and during ground testing of the structure. There are several approaches to the design of the spokes of the umbrella-type antenna [1–14]. Winding is the most technologically feasible method for manufacturing a thin-walled spoke. In the process of winding a strip of unidirectional composite material is laid layer by layer on a cylindrical mandrel at the angle ±ϕ to the longitudinal axis (fig. 2). With a large number of thin, alternating layers with angles +φ and –φ, the structure of a spoke wall can be considered homogeneous and orthotropic.

The main types of spoke deformation are bending in the zoy plane and bending in the zox plane. Bending in the zoy plane occurs when the spoke is loaded with forces that arise during the process of membrane tension. The membrane tension is the main load case for the umbrellatype antenna's spoke. Therefore, the stiffness of the spoke bending in the zoy plane should be greater than the stiffness of the spoke bending in the zox plane. Cross section

of constant thickness is not optimal for achieving maximum stiffness with a given mass.

Optimization of the cross-section geometric parameters of the umbrella-type antenna’s spoke. The authors propose to change the shape of the spoke crosssection by using sections of different thicknesses to increase the bending stiffness of the thin-walled spoke of the umbrella-type antenna while maintaining the specified design mass (fig. 3). An important circumstance is the fact that such a design is technologically feasible.

We connect the longitudinal axis of the spoke passing through the centers of the cross sections with the coordinate z counted from the base (fig. 2) and assign the crosssection of the spoke to the coordinate system xoy (fig. 4). To maintain the specified mass of the structure, it is necessary to ensure the equality of the cross-sectional areas of the spokes in question (fig. 4, 5), which can be achieved by using the cross-section shown in fig 4, 5. Formulas are obtained that allow estimating the bending stiffness of the spoke cross section in the case when the thickness varies stepwise (fig. 5).

Let us define the bending stiffness of the cross section of the spoke. Calculation of a thin-walled rod with a closed cross-sectional contour is carried out on the basis of the hypotheses of the beam theory, according to which the cross section is not deformed and turns like a hard disk when bending.

а                                                                b

Fig. 1. An umbrella-type antenna with spokes with a circular cross section: a – an antenna in the deployed position; b – the start position of an antenna

Рис. 1. Зонтичная антенна со спицами с круглым поперечным сечением: а – в развернутом положении; б – в стартовом положении

Fig. 2. A cantilever thin walled spoke with a round cross-section

\\\\\\\\\\\\\\\

Рис. 2. Консольная тонкостенная спица с круглым поперечным сечением

Fig. 3. An isometric view of the spoke with variable thickness

Рис. 3. Общий вид спицы с переменным сечением

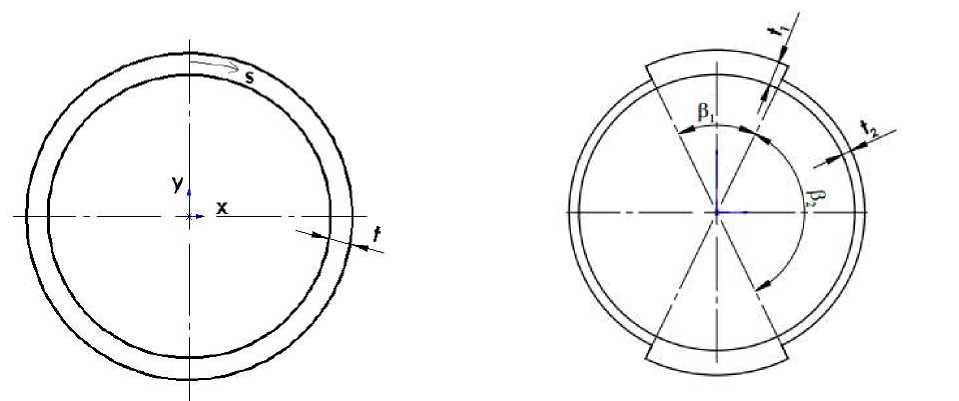
Fig. 5. A thin-walled round spoke with variable thickness in the cross section

Fig. 4. A thin-walled round spoke with constant thickness in the cross section

Рис. 4. Спица с гладким поперечным сечением

Рис. 5. Спица с переменным поперечным сечением

Within the framework of the beam theory [15], the bending stiffness of the cross-section in the planes zoy and zox are defined as follows:

D x = ( B_ii y ² ds , D y = ( B_ii x ² ds . (1)

Here s is the contour coordinate, which is calculated from the formula s = R β, respectively ds = Rd β. The value В 11 denotes the stiffness of the spoke wall when stretched or compressed in the axial direction.

After some transformations (5) we obtain the following expression:

Dx = AnR ³ ( t i ( p i + sin p i ) + 1 2 ( n- ( p i + sin p i ))).    (6)

Taking into account the equality of the cross-sectional areas of the two spokes under consideration, we obtain expressions for the bending stiffness of a spoke with a smooth cross-section:

x = R sin P , y = R cos P .           (2)

Substituting (2) into (1), we obtain the following expressions:

D_x = ( B_ii R ² cos² P Rd P = R ³ ( B_ii cos² P d P ,

D y = B_ii R² sin²pdp Rd p = R³( B_ii sin²p d p.    (3)

The rigidity of a spoke with a smooth cross-section will be expressed with the following form:

D = A n R ³ 1 ₂ ( n + P i ( a- i)),            (7)

and a cross-section with variable thickness:

D x = A n R ³ 1 2 (( a- i)( P i + sin p i ) + n ),       (8)

where α = t 1 / t 2 .

The bending stiffness relations can be written in the following form:

n =

D x D

= i +

sin P _i

n

P i ⁺---- 7

a- i

D = n B_ii R ³ = n A_utR 3 .              (4)

For a spoke with a complex cross-section (fig. 5), the expression for the bending stiffness of the cross section in the zoy plane takes the form:

D_x = 2 R 3

(

Ant i J cos P d P + An1 2

V

^+₽ 2

J cos² p d P +

5 l

⁺ A ii t i

2   22

J    cos² p d P

Pi у+e2

where β2 = π – β1.

The results of the calculations are shown in the graph (fig. 6) for different thickness ratios α. Here α₁ = 1.5, α 2 = 2.0, α 3 = 3.0, α 4 = 4.0, α 5 = 5.0.

As it can be seen from the graph, the maximum stiffness is achieved when the ratio of the thicknesses of the spoke with the variable cross-section is 5 and the angle β 1 is equal to 62°.

Modal analysis of the spokes by the finite element method was carried out (fig. 7) to verify the results. The spokes are made of CFRP (Carbon Fiber Reinforced Polymer) with the following characteristics: modulus of elasticity is 100 hPa, Poisson’s ratio is 0.3, and density is 1500 kg / m³. The internal diameter of the spoke is 200 mm, the length is 6 m, the thickness of the smooth cross-section is t = 2 mm.

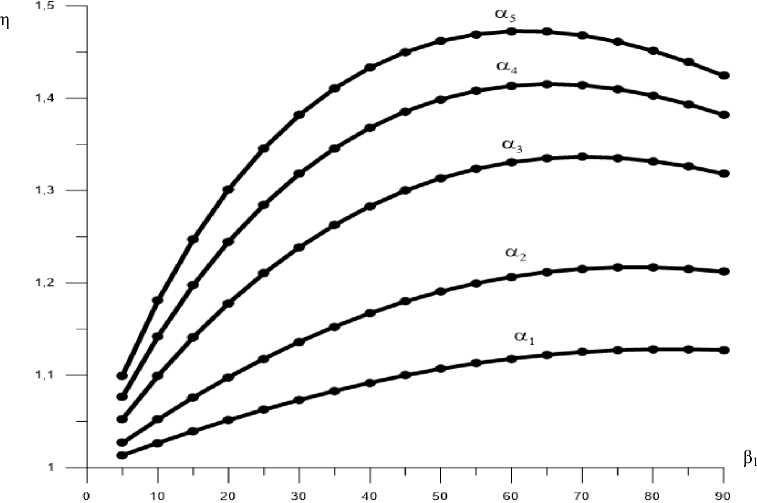
Fig. 6. The dependence of the stiffness parameter on the angle β 1 at different thickness ratios

Рис. 6. Зависимость жесткостного параметра от угла β ₁ при разных соотношениях толщин

Fig. 7. The modal analysis of a spoke with a variable cross-section

Рис. 7. Модальный анализ спицы с переменным поперечным сечением

Taking into account the equality of the areas of the two cross-sections, we obtain the parameters for a spoke with a variable cross-section: the angle β₁ is 60°, the thickness t ₁ = 4 mm and t ₂ = 1 mm. With these geometric parameters, the masses of the spokes are practically equal.

The first frequency of a spoke with a smooth crosssection is 8.69 Hz, and that of a spoke with a variable cross-section is 10.64 Hz. As a result of the calculation it can be seen that the stiffness of a spoke with a variable cross-section significantly increased in comparison with a spoke with a smooth cross-section. The ratio of stiffness obtained numerically is 1.47.

The conclusion. Substituting the calculated parameters of the spokes into expression (9), we obtain η₁ =1.41. Verification of the results obtained showed good convergence with theoretical conclusions.

Thus, the formulas obtained make it possible to estimate the bending stiffness of the cross-section of the umbrella-type antenna spoke when its thickness varies stepwise and give practical recommendations for the design of large expandable space antennas with improved parameters, namely, maximum stiffness with a minimum mass of the structure.

Acknowledgments. This work was supported by the Ministry of Education and Science of the Russian Federation № RFMEFI57517X0144.