Optimal Control of Model Reduction Binary Distillation Column

The distillation column is an essential unit operation used notably in chemical industries to separate solutions of compounds into individual elements primarily based on their one of a kind boiling point. With its large number of equations, this system can be viewed as large-scale chemical plant whose modeling and manipulate has been an interesting problem of study [1,2]. Optimal control problems, where the desired state is to be reached in minimum time, are important in the operation of engineering systems for example, in the distillation column, we may wish to reach the desired state of operation as fast as possible and with more stability [3].

Many optimization-based controllers have been proposed by researchers. model predictive control(MPC) are adopted for control of distillation columns since they allow to synthesize optimal control actions while simultaneously respecting constraints on manipulated variables and controlled outputs[4].

Nowadays, many centralized optimization algorithms, such as variation calculus-based methods, nonlinear programming and dynamic programming have been proposed for solving optimal control problems[5,6].[7] have studied the energy efficiency optimization for distillation column using artificial neural network models and showed that by having an accurate model the energy efficiency could be improved. In[8], an adaptive generalized predictive controller is designed to achieve the optimal operating conditions for controlling the packed distillation column for regulatory problems.[9] presents the design PID) controller, using the Biggest Log Modulus Tuning (BLT) in state space and calculating the controller as the Biggest Log Modulus Tuning algorithm.

• [10]    is presented a decentralized control scheme to achieve optimal and economic performance using controlling both pressure and temperature.[11]is presented an intelligent predictive controller, where a neural network predicts the behavior of the system and a genetic algorithm modifies the controller’s parameters based on an optimization problem.

2.    Distillation Column Model

The optimal manage problem studied in this paper is to carry the binary distillation response to minimal time, with less overshoot and satisfied the desired compositions at two sides of column (top and bottom).

There are many researchers are dealing with the optimization of distillation column.[12] showed that selfoptimizing control is a strategy for selecting controlled variables, but still the complex for a selection criterion to do it.[13] showed that for acceptable controller design, The accurate design of distillation columns is a very important, so that the model reduction plays an additional factor.[14] showed that using a tuning rule focusing on a genetic algorithm to determine the optimal PI/PID control settings for binary distillation column model to give easier procedure when compared with traditional optimization techniques. This problem, which can also be optimized by minimization of an (ISE) and (IAE) performances index, which area well known problem considered by many researchers. In this paper utilizes the soft-computing techniques (IWO) and (DE) which are more used for designing multivariable control systems to obtain the best optimal control, when compared with classical control methods.

The remainder of the paper is organized as follows: Section II presents the dynamic model of the distillation column. Section III presents model reduction of distillation column. Section IV explains the controller’s types for distillation process, classical and optimal. Section V presents the results and discussion, with a comparison between the controllers based on simulation results. Finally, Section VI contains the main conclusions.

The process considered relates to a distillation column, as shown in Figure 1, for separating a binary mixture of water and methanol. Wood and Berry is more practical column used until now for many studies and control [12,13.14,15].

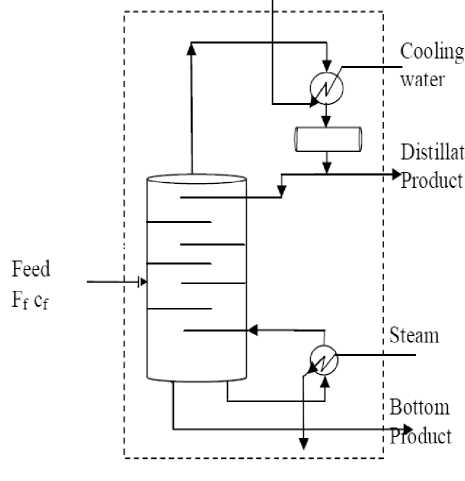
Fig.1. Schematic diagram of binary distillation column

The model consists of 8 plates, plus a condenser and a reboiler. The control is achieved by changing the heat input to the reboiler and the heat withdrawn from the condenser. There are two control variables (XD for top)and(XB for bottom) and two manipulated variables(Reflux rate L)and(steam rate V).Generally ,the matrix system is[16]:- й=■ < 8 ]

Where G ( 5 ) = [^ ⁽S) ^ (S)] is the system matrix

For Wood and Berry is:-

G ( 5 ) = I

12.8e-s

- 18.9 e-s

16.7S+1

6.6e-7s

21 s+1

-19.4e-3s

. 10.9S+1

14.4S+1

]

Since the G(s) is multivariable system, so that there are interaction between the loops, where change the input (L) to control (XD),the (XB) also change, in this state, a decoupling is needed to prevent it. There are many decoupling schemes were developed during past 30 years for two-input two-output (TITO) systems and have been well-summarized in many literature and process control textbooks[17,18,19].In this paper, the simplified decoupler is used, because it is simple and direct calculated ,but the main disadvantage is resulted a big dimension of decoupler matrix.

A. Simplified Decoupling

This decoupling control design, called "simplified decoupling" by Luyben [20], is widely used in the literature. It consists in selecting the decoupler as follows:

D ( s )=

[1я

^1

L 522

The resulting transfer matrix decoupler T ( s ) is:-

T ( s )=

|5u(s)

5 12 (5)5 21 (5) 022 ^(s)

0 22⁽ S)

—

5 12 (5)5 21 (5) 5 11 (5)

I

This choice makes the realization of the decoupler easy, but the diagonal transfer matrix T ( s ) obtained is complex since its elements are the sum of transfer functions. Controller tuning can therefore be difficult. It is then often suggested to approximate each sum by a simpler transfer function to facilitate controller tuning. Taking WB column , equ(2),and using equ(3),the decoupler is:-

D ( s )=

[,

0.33(14.25+1)6 ^4S

L 10.895+1

1.476(16.75+1)6

16.75+1

I

Then, according to equation (4), the diagonal matrix of WB column is given by

511 (s)=

12.8e-s

16.75 + 1

6.237(14.365+1)e-7s

228.695 2 + 31.895+1

522 (s)=

-19.4e-3s

14.45 + 1

9.745(16.75+1)e-9s

228.695 2 +31.895+1

To simplify the equations in (6) and (7), pade approximation is used to remove the nonlinear term in equations by using the following equation [21]:-

e1-fc e ~ 1+ 2,

-12.8 s + 25.6

16.7 52 + 34.4 s + 2

And the second term of equation (6) becomes:-

-89.56 52 + 19.35 s + 1.782

228.7 53 + 97.23 52 + 10.11 S + 0.2857

By the summing the equations (9) and (10) the result is:-

_      -1432 54+ 7368 53 + 1843 52+ 155.2 s + 3.75

^11WB 3819 5 5 + 9491 5⁴ + 39715 3 + 547.15² + 30.05 s + 0.5714

Also the first term of equation (7) becomes:-

19.4 5-12.93

14.45 2 +10.6 5+0.6667

And the second term of the equation (7) becomes:-

162.7S 2 +26.42 S+2.166

228.7s³+82.71 S 2 + 8.087 S+0.2222

By the summing the equations (12) and (13) the result is:-

G 22WB =

2093 S⁴—2698 s³-710.1 s²-59.71 S-1.43

3293S 5 + 3615 S 4 + 1146 S 3 + 144.1 S 2 + 7.747 S+0.1481

It is seen that, they obtained equations (11,14) are of high order and these made complex and difficult to design and analysis, so model reduction techniques is used to reduce the order of these equations.

3.    Distillation Column Model Reduction

In this work, we present a highly-accurate technique of model order reduction applied to distillation column. The proposed method reduces the dimension of the original system based on Evolutionary Algorithm (EA) which is a generic population-based meta-heuristic optimization algorithm. An EA uses some mechanisms inspired by biological evolution: reproduction, mutation, recombination, natural selection and survival of the fittest. In this type of reduction, there are many methods; Genetic Algorithms(GA) and Particle Swarm Optimization(PSO) are two famous Evolutionary Algorithms [22].In this work, (PSO) is used.

PSO is a biologically inspired algorithm and it is a population based stochastic nature. Each individual is referred to a particle and can move in the search space in all the directions in such a way that it reaches optimal solution. The steps of PSO algorithm are used [23].MTLAB package to execute, with the following parameters:-

Generation count limit=200, population size=50, problem dimension=5, mutation probability=0.06, number of elites=2, after exploitation improvement program, the reduced transfer function for applying PSO algorithm to equation (11)is :-

0.8498s+0.5051

G   =

^11rWB   s²+0.9989s+0.077

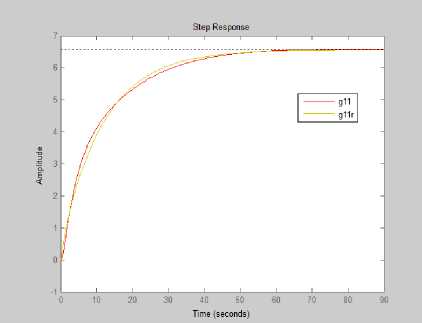
Fig.2. shows step response comparison of original G 11WB and reduced order system G 11rWB

Table.1 Transient specifications comparison

Characteristics	G 11WB(original)	G 11rWB(proposed)
Ts	48.4	45.8
Tr	27.5	25.8
Mp	0.273%	0.272%
Ess	6.43	6.43

And for equation (14) is :-

0.73245 - 1

*^ . * .•      ^ - '         -ж-

G   =

0.78115 2 + 1.0475+0.1049

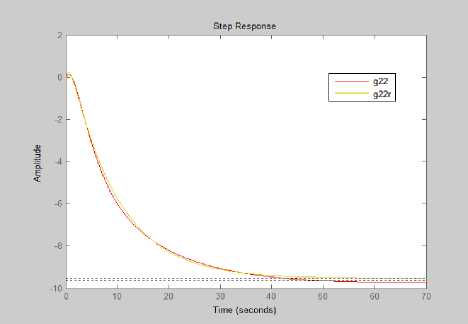
Fig.3. shows step response comparison of original G 22WB and reduced order system G 22rWB

Table.2 Transient specifications comparison

Characteristics	G 22WB(original)	G 22rWB(proposed)
Ts	40.7	37.2
Tr	21.5	20.2
Mp	0.65%	0%
Ess	-0.193	-0.193

As seen from figs(2,3) and tables(1,2), the reduction models by the proposed method of Wb are very close to the original model specially in settling and rise time.

4.    Control Strategies for Distillation Column System

There are many control strategies applied to distillation column multivariable system[24,25]:-

• •    Centralized structure

• •    Decentralized structure

• •    Decoupled structure

In this paper , Decentralized Decoupling structure control strategy is used, where the proposed algorithm involves combination of simplified decoupler , and decentralized controller with optimal PI design with model reduction of the effective transfer function, for the models under test. Fig(4) shows controlled structure block-diagram .

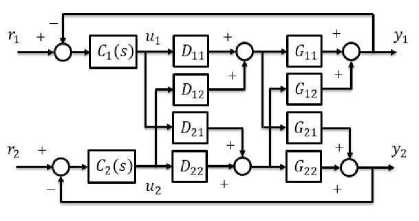
Fig.4 shows controlled structure block-diagram

For Tuning of Controller (PI) Parameters C1(s) and C2(s) based on Optimization Algorithms, The optimal parameters of the PI (Kp, Ki) can be obtained by applying DE and IWO algorithm. The DE and IWO algorithms are depended on the fitness function (performance index). Generally there are many types of performance index, but in this work using only:-

SSE_r = J ” e ² (t)dt                                             (17)

AAE = ^ ” |e| dt                                             (18)

These fitness functions are adopted to find the fitness of each solution in population size for both DE and IWO algorithms.

For design specifications, it is required to reach minimum overshoot(Mp%),stable system behavior and speedy responses settling time(Ts) and more accuracy system, zero steady-state error.

DE Algorithm

In [26] is proposed a new floating point encoded evolutionary algorithm for global optimization and named it DE owing to a special kind of differential operator, which they invoked to create new offspring from parent chromosomes instead of classical crossover or mutation. The parameters of the DE determined by trial and error with its specific ranges are listed in Table.3.

Table.3 The DE algorithm parameters.

Parameters	Value
Problem dimension (D)	5
Population size (NP)	25
Crossover constant (CR)	0.6
Scaling constant (F)	0.95
Number of generation (GEN)	20

IWO Algorithm

(IWO) Optimization algorithm was first introduced in [27]. Weeds invade the fields by dispersing their seeds with the help of air. These seeds occupy the available spaces and grow into flowering weeds by utilizing the available resources. Those weeds that adapt well to the environment produce more seeds than others. These new weeds are dispersed randomly in the field and they grow into flowering weeds and the process continues. This competition among the weeds makes them adapt well to the environment [28]. The parameters of the IWO determined by trial and error with its specific ranges are listed in Table.4.

Table. 4 The IWO algorithm parameters.

Parameters	Value
Number of Generation	20
Initial Population Size	2
Maximum Population Size	10
Minimum Number of Seeds	0
Maximum Number of Seeds	5
Initial Value of Standard Deviation	0.5
Final Value of Standard Deviation	0.001

5.    Simulation Results and Discussion

This part demonstrates and discusses the suggested controller’s simulation results and this is done using Matlab simulation package.

• A.    Controlling XD for G 11rWB

It is required to find the optimal values of the PI controller gains (Kp, Ki) to minimize the ISE and IAE performance indices using DE, IWO. Assume the input =0.98 with lower and upper bounders [20 20], [30 30 ] respectively for DE-PI and with lower and upper bounders [0 0 ], [10 10] respectively for IWO-PI. Firstly, using MATLAB tool for the model (wood and berry g11rWB), to find the PI parameters controller, the results are depicted in

Table.5 The optimal parameters of PI controller for G 11rWB using performance index ISE

Controller type	К р	К	Average No. of Iteration
PI-MATLAB	0.0764	0.0242
DE-PI	29.9777	28.8345	15
IWO-PI	4.8755	2.0777	15

Table 6 Transient response parameters of G 11rWB for ISE

Controller types	Mp%	Ts(minute)	Tr(minute)	Ess
Without controller	0.13	3.67	7.72	0.13
PI-MATLAB	12.4074	46.6524	13.8450	0
PI-DE(ISE)	1.2039	1.9683	0.7905	0
PI-IWO(ISE)	3.1146	4.9061	0.5105	0

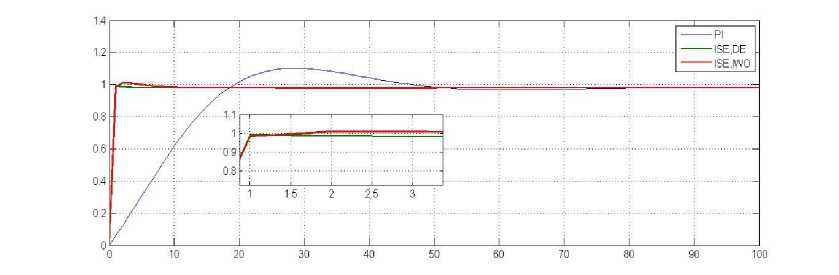
Fig.5 Step Response of PI Controller and PI Controller using DE, IWO for ISE

Table.7 The optimal parameters of PI controller for G 11rWB using performance index IAE

Controller type	К р	Kt	Average No. of Iteration
PI-MATLAB	0.0764	0.0242
DE-PI	24.501	24.601	15
IWO-PI	5.1002	5.0121	15

Table.8 Transient response parameters of G 11rWB for IAE

Controller types	Mp%	Ts(minute)	Tr(minute)	Ess
Without controller	0.13	3.67	7.72	0.13
PI-MATLAB	12.4074	46.6524	13.8450	0
PI-DE (IAE)	2.3725	0.6299	0.0977	0
PI-IWO (IAE)	7.9654	3.1801	0.3889	0

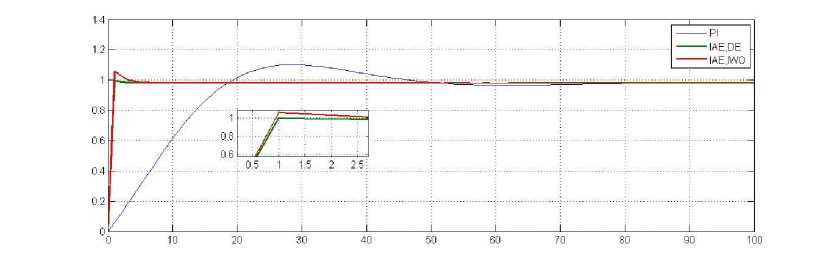
Fig.6. Step Response of PI Controller and PI Controller using DE, IWO for IAE

Figure (5) illustrates the responses of the three controllers when the performance index is ISE. As shown in this figure, the system with MATAB- PI controller gives overshoot 12.4074%, rise time 13.8450 min, and settling time (2% criterion) 46.6524 min. While the system with PID-DE controller results in less overshoot 1.2039%, less rise time 0.7905min, and settling time 1.9683min and for IWO , give also best result, when compared with the MATLAB-PID, but not best than using PID-DE as shown in table.6.For figure (6),the same conclusion can be reached, but the sates for the undershoot values are increased for IAE .

The DE and IWO algorithms are better than PID tuner by MATLAB in transient response specifications , and by all optimal criteria ISE and IAE. Moreover, among these performance indices, the IAE one is more capable than the other in providing minimal overshoot, low rise time and low settling time for the transient response system.

• B.    Controlling XB for G 22rWB

The same procedures as in 5.1. Assume the input =0.02 with lower and upper bounders [-1 -1], [0 0] respectively. The results are depicted in Table.9 and transient response specifications are shows in Table.10 for ISE, while table.11 and table.12 for IAE. Fig.7 and 8 shows step response controlled system for ISE and IAE respectively.

Table.9 The optimal parameters of PI controller for G 22rWB using performance index ISE

Controller type	КР	K t	Average No. of Iteration
PI-MATLAB	-0.1632	-.0286
DE-PI	-0.5009	-0.471	15
IWO-PI	-0.4331	-0.0465	15

Table.10 Transient response parameters of G 22rWB for ISE

Controller types	Mp%	Over shoot	Ts(minute)	Tr(minute)	Ess
Without controller	N/A	N/A	N/A	N/A	N/A
PI-MATLAB	9.4941	3.7694	26.3414	6.0747	0
PI-DE(ISE)	17.5423	5.3579	12.4342	1.9069	0
PI-IWO(ISE)	17.3862	11.9319	11.3989	1.7797	0

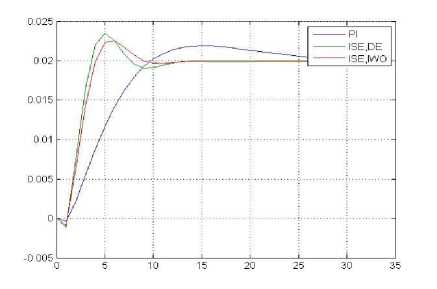
Fig.7. Step Response of PI Controller and PI Controller using DE, IWO for ISE

Table.11 The optimal parameters of PI controller for G 22rWB using performance index IAE

Controller type	К р	K t	Average No. of Iteration
PI-MATLAB	-0.1632	-.0286
DE-PID	-0.2717	-0.028	15
IWO-PID	-0.5101	-0.0469	15

Table.12 Transient response parameters of G 22rWB for IAE

Controller types	Mp%	Over shoot	Ts(minute)	Tr(minute)	Ess
Without controller	N/A	N/A	N/A	N/A	N/A
PI-MATLAB	9.4941	3.7694	26.3414	6.0747	0
PI-DE (IAE)	0	6.2333	7.7918	4.3258	0
PI-IWO (IAE)	17.9261	12.1463	11.3792	1.7423	0

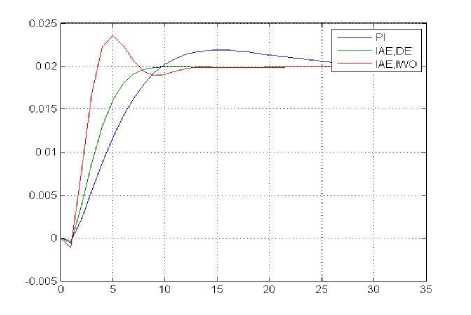
Fig.8. Step Response of PI Controller and PI Controller using DE, IWO for ISE

According to tables (10),(12) ,The DE and IWO algorithms are better than PID tuner by MATLAB in transient response specifications in produce low rise time and low settling time and as seen in figs(7) and(8) and by all optimal criteria ISE and IAE. Moreover, among these performance indices, the IAE one with DE algorithm is more capable than the other in providing minimal overshoot, low rise time and low settling time for the transient response system but with bigger under shoot than the state with MATLAB-PID tuner.

6.    Conclusions

In this paper, we have shown how to control a distillation column using optimization algorithms, Interaction between the two loops of distillation column was recommended, so we use simplified decoupling in order to eliminate the interaction between loops and to make the system stable. The decouplers are greatly improved the response of the system. PSO have been employed to optimize a model reduction of the large-scale dimension of distillation process by selecting the best model structures for numerator and denominator transfer function. PI-DE controller showed more advantages than PI-IWO related to transient specifications for controlling top composition (XD) with IAE performance index and PI-DE also showed the same advantages, when compared with PI-IWO for controlling bottom composition (XB),with IAE.This comparison showed clear difference through the curve of the response and the values of the absolute mean square error and the integral square error. There is some undershoot response with starting dynamic for controlling (XB), because the G22rWB system is non-minimum phase (one zero in right hand side of s-plane). Generally Decentralized has the advantages of simplicity (two PID controllers) for binary column and less solution time than the centralized method, which needs four PID controllers and more tuning for each loop. Thus the top and bottom composition of distillation column is controlled and desired performance is achieved.

Acknowledgment

The authors would like to thank Mustansiriyah University ( Baghdad – Iraq for its