Оптимальная 2D-расстановка виртуальных объектов в физическом пространстве для приложений дополненной реальности

Введение. Научные и прикладные работы о размещении виртуальных объектов в реальном пространстве чаще всего фокусируются на вопросах интерактивности, интеграции реальности и виртуальности, физических свойствах виртуальных элементов. Однако недостаточно проработана задача одновременно свободного и оптимального размещения объектов с учетом их размеров и окружающей зоны комфортности вокруг них. В литературе можно найти описание схожей задачи — об упаковке в прямоугольный контейнер. В нашем случае цель не ограничивается максимально плотным размещением. Следует учесть два условия: жесткие размеры объектов (их запрещено нарушать) и дополнительные области — зоны комфортности (их нежелательно занимать). Цель работы — создание и реализация такого 2D-алгоритма размещения объектов в физическом пространстве, который будет учитывать обозначенные выше ограничения.

Материалы и методы. Используя аппарат численных методов, авторы задействовали созданный ранее 1D-алгоритм размещения объектов. Расчеты основываются на системе линейных уравнений. В одномерном случае оптимальное размещение виртуальных объектов сводится к задаче, не зависящей от вида функции комфортности. Элементы такой системы — размеры объектов, дистанции между ними, а также расстояния до края области встраивания, зоны комфортности. Предлагаемый 2D-алгоритм оптимальной расстановки виртуальных объектов реализовали в виде программного кода на языке C# с использованием известного игрового движка Unity . Решение тестировали на гаджетах в режиме пиковой нагрузки для 5, 10, 15, 20, 25, 35, 40, 45 и 50 объектов. Для опытов задействовали 1,8 тыс. устройств. Проанализировали около 77 тыс. событий. Чтобы исключить нерепрезентативные значения, каждый расчет повторяли 10 раз, и для каждого значения провели z -оценку. Аномальные (больше 3 и меньше –3) исключили.

Результаты исследования. В работе создан алгоритм 2D-расстановки, который реализует заполнение прямоугольной области виртуальными объектами. У каждого из них есть размер и еще одна характеристика — зона комфортности. Авторы составили блок-схему реализации данного алгоритма в заданной двумерной левосторонней системе координат. Показано, в частности, на каком этапе объекты сортируются по длине, когда формируются их партии и выполняются расстановки по двум осям. Первая — горизонтальная, вторая направлена вперед от пользователя (это вектор глубины, или фронтальное измерение). Алгоритм 1D-размещения для сформированного ряда позволяет оптимально расположить объекты вдоль оси X на основе рассчитанного коэффициента комфортности К. Выполнены расчеты и составлены схемы с целью достичь определенных показателей комфортности. Для каждого объекта первой линии смещение по оси Z от края плоскости определяется так, чтобы комфортность спереди равнялась комфортности по X . Начиная со 2-го ряда для вычисления отступа проверяется наличие потенциальных соседей, которые находятся на ряд выше и имеют общие участки по X с обрабатываемым объектом. Каждый элемент строки устанавливается по оси Z так, чтобы его комфортность сверху была максимальной из односторонних горизонтальных комфортностей в данной и предыдущей строках. Принцип расчета координаты Z для объекта строки представлен в виде блок-схемы.

Исходными данными для реализации этого алгоритма были 7 объектов с 14 разными размерами и 28 зонами комфортности. После программной реализации работу описанного 2D-алгоритма проверили на практике — в мобильном приложении дополненной реальности. Записали аналитические данные пользовательских сессий. Рассчитали среднее время выполнения. Возникшую в ходе работы гипотезу о квадратичной зависимости проверили на персональном компьютере. С этой целью провели аналогичный эксперимент для диапазона [10– 10000] объектов. Гипотеза подтвердилась. Алгоритму можно присвоить сложность O( n ²). Для сравнения скорости вычисления задействовали 10 самых популярных моделей пользовательских устройств. Результаты представили в виде диаграммы. Минимальное зарегистрированное время выполнения — 0,093 мс, максимальное — 0,146 мс. Расчеты показали высокую эффективность двумерного алгоритма. Дополнительно визуализировали схемы расстановки для разного количества и параметров объектов.

Обсуждение и заключение. Предлагаемый алгоритм двумерного размещения позволяет работать с набором виртуальных объектов с разными размерами и зонами комфортности. Показаны достаточно высокие производительность и стабильность. В среднем алгоритм реализуется за доли миллисекунды даже при больших партиях объектов. Возможные будущие направления работы:

• -    расширение подхода для построения 3D моделей и алгоритмов;

• -    включение в алгоритм вращения объектов для большей гибкости их расположения и лучшего использования пространства.

Итоги работы могут представлять интерес для инженеров и дизайнеров интерфейсов. В перспективе следует изучить пользовательский опыт и возможности включения дополнительных ограничений на позиционирование.

Original article

Optimal 2D Placement of Virtual Objects in Physical Space for Augmented Reality Applications

Информатика, вычислительная техника и управление

Marianna V. Alpatova   В , Yuri V. Rudyak О

Moscow Polytechnic University, Moscow, Russian Federation

Introduction. Research and applied works on the placement of virtual objects in real space most often focus on issues of interactivity, integration of reality and virtuality, physical properties of virtual elements. However, the task of simultaneously free and optimal placement of objects, taking into account their size and the surrounding comfort zone, has not been sufficiently worked out. In the literature, you can find a description of a similar task — about packing in a rectangular container. In our case, the goal is not limited to the greatest possible dense placement. Two conditions should be taken into account: rigid dimensions of the objects (it is forbidden to violate them) and additional areas — comfort zones (it is undesirable to occupy them). The work aims at creating and implementing such a 2D algorithm for placing objects in physical space, which takes into account the above limitations.

Materials and Methods. Using a set of numerical methods, the authors applied the previously created 1D algorithm for the placement of objects. Calculations were based on a system of linear equations. In the one-dimensional case, the optimal placement of virtual objects was reduced to a task that did not depend on the type of comfort function. The elements of such a system were the dimensions of objects, the distances between them, as well as the distances to the edge of the embedding area, a comfort zone. The proposed 2D algorithm for optimal placement of virtual objects was implemented in the form of a program code in C# using the well-known Unity game engine. The solution was tested on gadgets in peak load mode for 5, 10, 15, 20, 25, 35, 40, 45, and 50 objects. 1.8 thousand devices were used for experiments. About 77

thousand events were analyzed. To exclude unrepresentative values, each calculation was repeated 10 times, and a z -score was performed for each value. Abnormal events (more than 3 and less than -3) were excluded.

Results. In this paper, a 2D placement algorithm that implements filling a rectangular area with virtual objects has been created. Each of the objects had a size and another characteristic — a comfort zone. The authors compiled a flowchart for the implementation of this algorithm in a given two-dimensional left-hand coordinate system. It was shown, in particular, at what stage objects were sorted by length, when their batches were formed, and arrangements were made along two axes. The first axis was horizontal, the second was directed forward from the user (this is the depth vector, or frontal measurement). The 1D-placement algorithm for the generated row provided optimal positioning the objects along X -axis based on the calculated comfort coefficient К. Calculations were made and schemes were drawn up to obtain certain comfort indicators. For each object of the first string, the displacement along Z -axis from the edge of the plane was determined so that the comfort in front was equal to the comfort along X . Starting from the 2nd row, to calculate the displacement, the presence of potential neighbors who were a row higher and had common areas along X with the object being processed, was checked. Each element of the string was set along Z -axis so that its comfort from above was the maximum of the one-sided horizontal comfort in this and the previous strings. The principle of calculating Z coordinate for a string object was presented in the form of a flowchart. The initial data for the implementation of this algorithm were 7 objects with 14 different sizes and 28 comfort zones. After the software implementation, the operation of the described 2D algorithm was tested in practice — in an augmented reality mobile application. Analytical data of user sessions was recorded. The average execution time was calculated. The hypothesis of quadratic dependence that arose during the work was tested on a personal computer. For this purpose, a similar experiment was conducted for a range of [10-10,000] objects. The hypothesis was confirmed. The algorithm can be assigned a complexity of O( n ²). To compare the calculation speed, 10 of the most popular models of user devices were utilized. The results were presented in the form of a diagram. The minimum registered execution time was 0.093 ms, the maximum — 0.146 ms. Calculations showed high efficiency of the two-dimensional algorithm. Additionally, the placement schemes for different numbers and parameters of objects were visualized.

Discussion and Conclusion. The proposed algorithm of two-dimensional placement enables the user to work with a set of virtual objects with different sizes and comfort zones. Sufficiently high performance and stability are shown. On average, the algorithm is implemented in fractions of a millisecond, even with large batches of objects. Possible future focus areas:

• –    expansion of the approach for building 3D models and algorithms;

• –    inclusion of objects in the rotation algorithm for greater flexibility of their location and better use of space.

Acknowledgements. The authors appreciate the editorial team of the journal and the reviewer for their competent expertise and valuable recommendations for improving the article.

Funding information. The research was done with the financial support from RFFI within the framework of scientific project No. 21–510–07004.

Введение. Известная задача приложений дополненной реальности (augmented reality, AR) — размещение виртуальных объектов в реальном физическом пространстве. Ряд исследований [1–3] фокусируются на интерактивности, слиянии реальной и виртуальной сфер. Изучаются также вопросы физических свойств виртуальных объектов.

Недостаточно проработана задача такого размещения объектов, которое одновременно было бы свободным и оптимальным, учитывало не только геометрические размеры объектов, но и зоны комфортности вокруг них. В [6] отмечена внешняя схожесть этой задачи с известной задачей об упаковке в прямоугольный контейнер [5]. Однако есть существенная разница. В исследуемом случае недостаточно обеспечить максимально плотную упаковку. При размещении виртуальных объектов нужно учесть не только их жесткие размеры, которые нельзя нарушать, но и дополнительные области — зоны комфортности. Их занимать нежелательно. Эти дополнительные области позволяют приблизиться к объекту и выполнить с ним какие-то действия.

Целями представленной работы являются создание, реализация и оценка 2D-алгоритма оптимального размещения виртуальных объектов в физическом пространстве.

Материалы и методы. Ранее [4] авторы определили, что такое комфортное размещение виртуальных объектов, ввели понятие функции комфортности k ( x ). Она монотонно возрастает от 0 до 1 при 0< x <1 и равна 1 при х >1, где x = X ' D , X — расстояние от края объекта до ближайшего препятствия, D — размер зоны комфортности. Для каждого измерения у объекта есть две односторонние зоны комфортности D - и D +. Комфортность с каждой стороны вычисляется отдельно.

В [6] показано, что задача одномерного размещения n виртуальных объектов в свободной области пространства протяженностью L сводится к системе линейных уравнений, не зависящих от вида функции комфортности k(x):

X ^{( 1 )} X ^{( 2 )}

D F"

X ( i ) X ( i ^{+ 1 )}

• ^- "D +r,

l - £( x ^{( i )} + 1 ^{( i )})

X ( n )       ^^\ ^-

D - ⁿ ) ^-        D + ⁿ )

Здесь X-1) — расстояние первого объекта от левого края области встраивания; X-i), i - 2,3,...,n — расстояние между объектами с номерами i и (i - 1); D-‘) и D(‘) — левая и правая зоны комфортности соответственно; 1(i) — размер объекта; D+i) - D-i+1) - D+i) + D-i+1), i = 1,2,..., (n - 1).

Матрица системы (1) сильно разрежена, поэтому можно избежать использования не самых быстрых универсальных методов и достаточно просто найти решение. Например, в первых ( n - 1) равенствах можно в каждом i- м уравнении выразить X - ^{1 + 1 )} через X - i ) , затем подставить это в последнее уравнение и получить линейное уравнение относительно X - ¹ ) . После этого от первого уравнения к ( n - 1)-му последовательно определяются значения X - ^{2 )} , X - ^{3 )} ,..., X - n ) . Авторы реализовали данный ID-алгоритм размещения объектов с помощью численных методов. Он показал высокую скорость и эффективность. Этот 1D-алгоритм стал основой для научных изысканий, описанных в представленной работе. Авторы предложили 2D-алгоритм оптимальной расстановки виртуальных объектов. Его реализовали в виде программного кода на языке C# с использованием игрового движка Unity , который широко используется для создания мобильных приложений дополненной реальности [8]. В ходе эксперимента на устройстве пользователя, работающего в режиме пиковой нагрузки, запускался алгоритм для 5, 10, 15, 20, 25, 35, 40, 45 и 50 объектов. Замеряли время, затраченное на вычисления (в миллисекундах). Каждый расчет повторяли 10 раз во избежание аномальных значений. Всего в эксперименте участвовали 1,8 тыс. устройств, с них собрали и проанализировали около 77 тыс. событий с результатами.

Фильтрация аномалий с помощью z -оценки позволила выявить значения, которые можно определить как выбросы [9]. Авторы стандартизировали данные и вычислили z -оценку для каждого значения. Аномальными сочли те, у которых z -оценка оказалась больше 3 или меньше -3. Их исключили и сосредоточились на типичных и репрезентативных данных.

Результаты исследования. Итак, на плоскости X , Z есть прямоугольная область с шириной L x и длиной L z . Ее следует заполнить некоторым количеством виртуальных объектов. Каждый объект помимо своих размеров l x ‘ ) и 1 z ) (где i — номер объекта) характеризуется еще зонами комфортности D x - , D x + ,D z - ) , D + . На рис. 1 представлена блок-схема описываемого алгоритма.

Информатика, вычислительная техника и управление

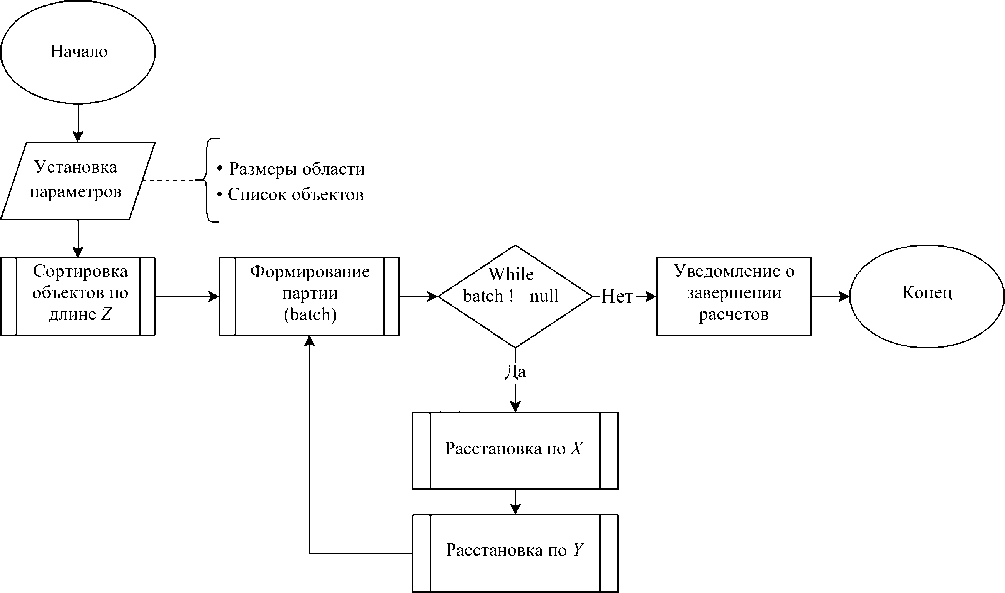
Рис. 1. Верхнеуровневый алгоритм 2D-расстановки

В данной работе используется левосторонняя система координат: ось X обозначает горизонтальный вектор размещения, ось Z направлена вперед от пользователя и является вектором глубины или фронтальным измерением [7]. Объекты размещаются в горизонтальной плоскости (например, на полу, столешнице и пр.), поэтому вертикальная ось Y не рассматривается, а все иллюстрации предполагают вид сверху на получившуюся композицию.

В левом нижнем углу каждого виртуального объекта обозначим опорную точку (pivot). Она будет определять конечные координаты размещения объекта. Далее набор объектов сортируется в порядке убывания по lZi) + dZ- + dZ + — габаритной длине объектов с учетом зон комфортности, расположенных спереди и сзади

в соответствии с рассматриваемой осью координат. После сортировки объекты, занимающие больше пространства по глубине, располагаются дальше от пользователя (или выше для схемы, представленной в горизонтальной проекции). Блок-схема формирования партии из объектов представлена на рис. 2.

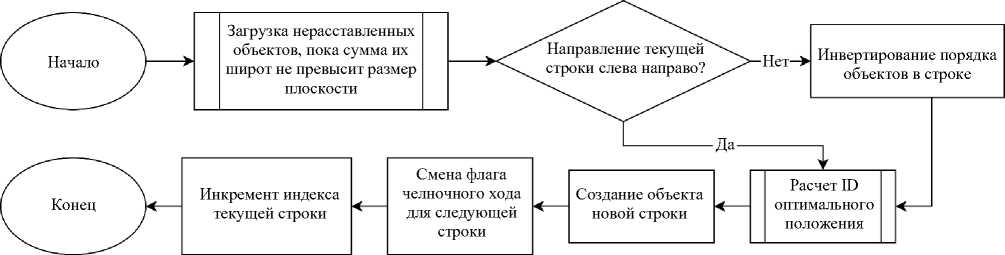
Рис. 2. Алгоритм формирования ряда из объектов

Затем из упорядоченного множества объектов формируются отдельные строки или партии (batch). В каждую строку включается минимальное количество объектов, сумма ширины которых вместе с зонами комфортности превосходит ширину заполняемой области L_x . Если при добавлении следующего объекта вычисленная занимаемая ширина превысит горизонтальный размер доступного пространства внутри прямоугольника, партия считается завершенной. Таким образом, каждая партия может быть размещена в виде линии в пределах области. Ряды чередуются слева направо и справа налево для смешивания крупных и мелких объектов. Это можно назвать «челночным ходом» (рис. 3).

Рис. 3. Схема «челночного хода» на координатной плоскости

Для сформированного ряда применяется алгоритм 1D-размещения, который позволяет оптимально расположить ряд объектов вдоль оси X на основе рассчитанного коэффициента комфортности К , одинакового для всех объектов ряда. Для каждого объекта первой линии смещение по оси Z от края плоскости определяется таким образом, чтобы комфортность спереди равнялась комфортности по X :

Z ( 1 )     X ( 1 ) z ( i )     X ⁽ i )

DT ж • Dza = ж ^{,i = 2Д}.", n

Начиная со 2-го ряда для вычисления отступа Z + проверяется наличие потенциальных соседей сверху из вышележащего ряда, имеющих с текущим обрабатываемым объектом общие участки по координате X . При этом каждый объект размещаемой строки устанавливается по оси Z таким образом, чтобы его комфортность сверху была максимальной из односторонних горизонтальных комфортностей в данной и предыдущей строках. Алгоритм расчета координат Z представлен на рис. 4.

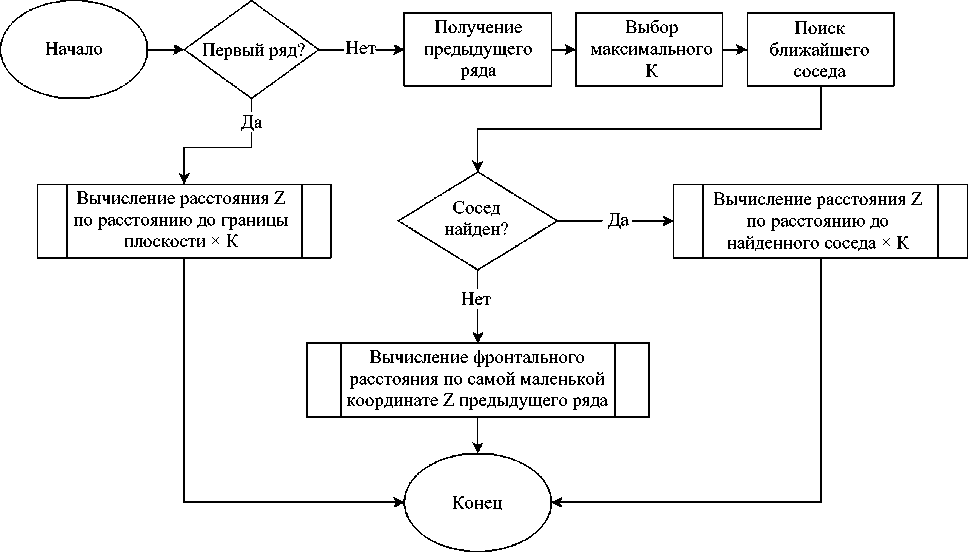
Рис. 4. Принцип расчета координаты Z для объекта строки

Из блок-схемы видно, что отступ вычисляется аналогично для всех трех возможных сценариев:

• –    отступ от края плоскости для установки объекта;

• –    отступ от соседа сверху;

• –    при отсутствии соседа в предыдущей строке берется самый близкий по Z объект из всех предыдущих строк.

  Информатика, вычислительная техника и управление

  
  

Новые партии формируются до тех пор, пока всем объектам не присвоят ряд или пока не закончится физическое пространство.

Исходные данные к описанному алгоритму систематизированы в таблице 1. Объекты рассортированы по их вертикальным размерам.

Таблица 1

Исходные данные к примеру работы описанного алгоритма

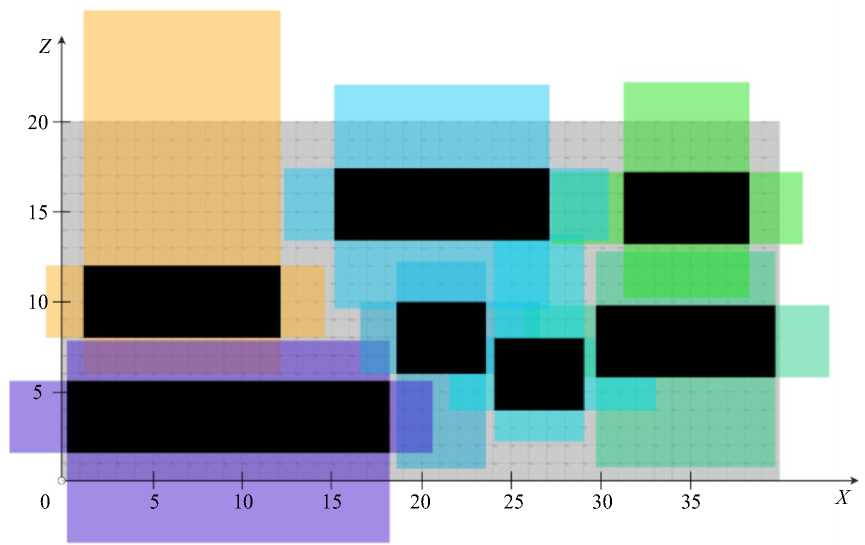
Рис. 5. Схема расположения объектов для рассматриваемого примера. Вид сверху

Номер объекта	Размер	Зона комфортности
1	(7; 4)	(4; 3; 3; 5)
2	(10; 4)	(4; 3; 5; 3)
3	(5; 4)	(2; 3; 5,25; 2,25)
4	(12; 4)	(2,8; 3,3; 3,8; 4,65)
5	(5; 4)	(2,5; 4; 1,75; 5,8)
6	(18; 4)	(3,2; 2,4; 5; 2,25)
7	(11; 4)	(2,1; 2,45; 2; 14,2)

Таблица 1 соответствует рис. 5, демонстрирующему размещение объектов.

Серый прямоугольник — это свободная площадь, на которой расставляются объекты. Черные области — объекты в их габаритных размерах. Цветные, с наложениями, — предустановленные зоны комфортности для каждого объекта. Как отмечалось выше, зоны комфортности объектов могут частично перекрываться и выходить за пределы свободного пространства, но применяемый подход позволяет обеспечить баланс, чтобы в равной мере уменьшались комфортности различных объектов.

Напомним, что в данную модель входит понятие функции комфортности k ( x ). От нее не зависит полученная система уравнений (1), а значит и оптимальное размещение объектов. А вот значения односторонних комфортностей объектов определяются и их размещением, и видом функции k ( x ). Приведем два примера:

• –    в случае линейной функции k ( x ) односторонние комфортности объектов верхнего ряда рис. 5 оказываются равными 0,6;

• -    для зависимости -J 1 - ( x - 1 ) 2 — значение 0,9.

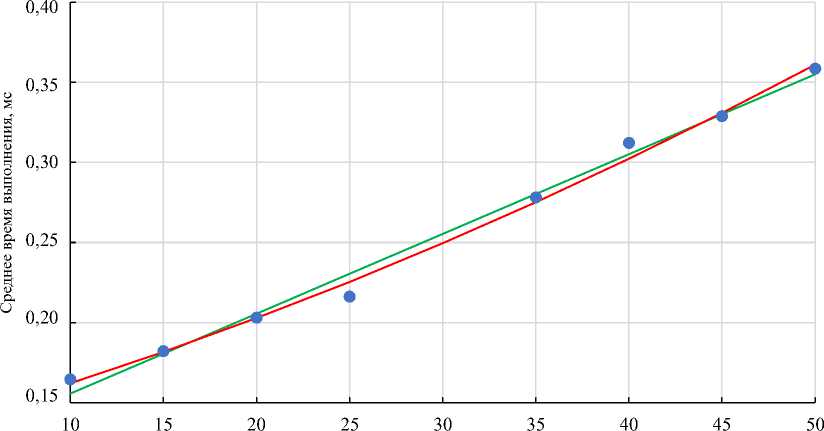
После программной реализации описанного 2D-алгоритма его внедрили в мобильное приложение с дополненной реальностью и записали аналитические данные пользовательских сессий. Сгруппировали информацию по каждой уникальной модели устройства, по каждому количеству расставляемых объектов в диапазоне [10–50]. Рассчитали среднее время выполнения (рис. 6).

Количество объектов

Рис. 6. Время выполнения алгоритма на пользовательских устройствах: • — реальные данные;----- a = 0,00498, b = 0,10593 — линейная аппроксимация; ––––– a = 0,00003, b = 0,00317, c = 0,12743 — квадратичная аппроксимация

На указанном диапазоне невозможно сразу определить точную сложность вычисления алгоритма. Как видно из рис. 6, данные близки к линейной и квадратичной аппроксимации. С помощью метода остаточной суммы квадратов рассчитана количественная оценка обеих аппроксимаций и получены значения 0,00035 и 0,00021 соответственно [10].

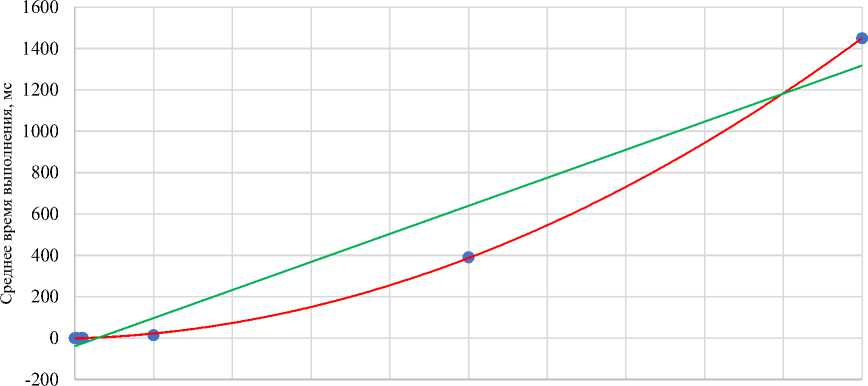
Для подтверждения гипотезы о квадратичной зависимости на персональном компьютере запустили аналогичный эксперимент для диапазона [10–10000] объектов. Рис. 7 подтверждает гипотезу, значит алгоритму можно присвоить сложность O( n ²). Впрочем, ситуация с 10000 объектами, скорее, теоретическая, и на практике в дополненной реальности пользователь вряд ли будет работать более чем с 1–2 десятками объектов.

0      1000    2000    3000    4000    5000    6000    7000    8000    9000    10000

Количество объектов

Рис. 7. Время выполнения алгоритма для большого количества объектов: • — реальные данные;----- a = 0,1365, b = –45,455 — линейная аппроксимация; ––––– a = 0,00001, b = 0,0103, c = –1,6178 — квадратичная аппроксимация

Сопоставили время выполнения на разных пользовательских устройствах. Отобрали 10 самых популярных моделей и по результатам вычислений построили диаграмму (рис. 8).

Информатика, вычислительная техника и управление

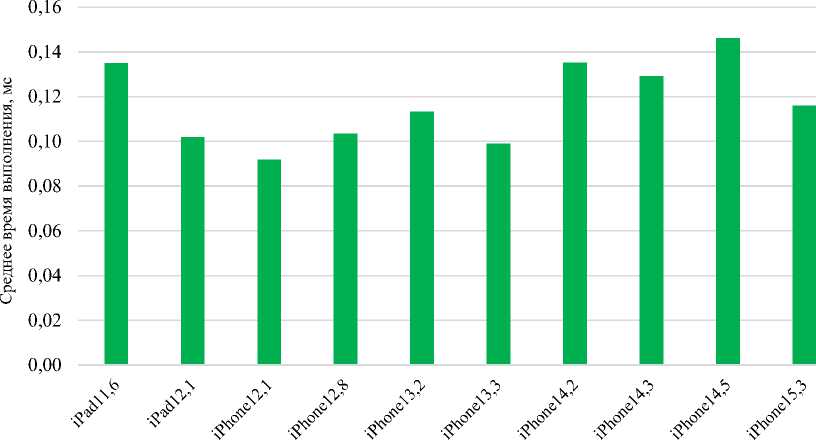
Рис. 8. Сравнение скорости вычисления на разных устройствах для 10 объектов

Минимальное зарегистрированное время выполнения — 0,093 мс, максимальное — 0,146 мс. Для данной выборки корреляция между моделью устройства и временем выполнения — всего 0,177. Это довольно низкое значение.

Расчеты показали высокую эффективность двумерного алгоритма. Это обусловлено разбиением всей совокупности объектов на отдельные строки и использованием в каждой строке быстрого одномерного алгоритма, описанного в начале статьи. Этот алгоритм позволяет решить задачу с меньшими затратами ресурсов и времени.

На рис. 9 представлены дополнительные визуализации схем расстановки для разного количества объектов и их параметров.

а )                                             б )                                                 в )

Рис. 9. Примеры расстановки разного количества объектов:

а — 4 объекта; б — 9 объектов; в — 21 объект

Итак, предлагаемый алгоритм двумерного размещения позволяет работать с набором виртуальных объектов. Каждый из них характеризуется определенными размерами и зонами комфортности. Алгоритм предназначен для оптимального расположения таких объектов в прямоугольном физическом пространстве, которое воссоздает окружение пользователя.

Обсуждение и заключение. Для ранее описанной одномерной задачи предложен и реализован в программном коде эффективный алгоритм оптимального размещения виртуальных объектов. Для двумерного случая построена модель оптимального размещения. На ее основе разработан эффективный алгоритм, реализованный в программном коде.

Проанализирована производительность алгоритма, которая измеряется временем выполнения. Установлено, что нет значимой корреляции между временем выполнения и моделью устройства. Среднее время — доли миллисекунды даже для больших партий объектов. Это говорит об относительно стабильной производительности алгоритма в различных условиях. Однако нельзя исключить возможное влияние других непроверенных факторов. Для полной характеристики зависимостей производительности нужны дальнейшие исследования.

Обозначим несколько направлений будущей работы для повышения производительности и адаптивности алгоритма. Это, во-первых, совершенствование решения, которое позволит использовать полные размеры объектов, по возможности без пересечений комфортных зон. Их размеры будут уменьшаться только в случае крайней необходимости. Это должно обеспечить оптимальное использование пространства и дальнейшее улучшение интерактивного опыта пользователя.

Во-вторых, включение вращения элементов в алгоритм повысит гибкость в их расположении и даст возможность лучше использовать пространство. К тому же это позволит алгоритму учитывать больше разных объектов, тем самым расширяя его практическое применение.

Заметим, что в приложении с дополненной реальностью расстановка пользователем трех и более объектов — достаточно трудоемкая задача. Она требует значительного времени и существенно затрудняет работу.

Предложенная технология размещения объектов в 2D позволяет оптимально позиционировать виртуальный контент для улучшения пользовательского опыта в дополненной реальности. Автоматизированный расчет расположения сокращает ручную работу и дает возможность сосредоточиться на полноценном взаимодействии с AR.

Научные изыскания в данном направлении ведут к бесшовной интеграции виртуального и физического пространств. Результаты могут применить на практике разработчики очков дополненной реальности, которые сталкиваются с проблемой быстрого интеллектуального позиционирования объектов в зависимости от пользовательских предпочтений и контекста. Кроме того, итоги работы могут представлять интерес для:

• -    инженеров, работающих над умными домашними системами;

• -    дизайнеров интерфейсов, для которых важно эффективно и гармонично сочетать элементы управления и информацию на экране.

Введение нечеткой логики позволяет разработчикам адаптировать решение под конкретные задачи и сценарии использования. В будущих исследованиях целесообразно изучить и задействовать пользовательский опыт, включать дополнительные ограничения на позиционирование объектов.