Оптимальная длительность импульсов в нелинейном волоконно-оптическом канале

Совершенствование технологии оптических волокон и создание одномодовых световодов с малыми потерями обеспечило возможности передачи информации со скоростями до нескольких гигабит в секунду. В цифровых системах связи основным фактором, препятствующим дальнейшему повышению скоростей передачи по волоконным световодам (как и по большинству других каналов связи), является дисперсионное расширение импульсов, резко возрастающее при уменьшении их длительности. Поэтому вызывает большой интерес предложенный сравнительно недавно метод компенсации дисперсионных деформаций за счет нелинейных явлений, возникающих при передаче импульсов большой интенсивности [1—3] . По предварительным оценкам, приведенным в [2] , использование солитонов - стационарных импульсов, формирующихся при полной взаимной компенсации дисперсионных и нелинейных деформаций в условиях пренебрежимо М^ЛЫХ потерь, позволит повысить скорость передачи на 1-2 порядка по сравнению с лучшими линейными системами. Большой интерес представляют и нестационарные режимы эволюции [3] .

Недостатком предложенных оценок скорости передачи является то, что они получены без учета нелинейного взаимодействия соседних импульсов в составе пакета сообщения: скорость рассматривается как величина, обратная минимальной длительности одиночного импульса. Однако необходимость учета такого взаимодействия не вызывает сомнений. В частности, в [4] предложено для его уменьшения сдвигать фазы соседних импульсов на ц, но при длительностях порядка нескольких пикосекунд осуществить это технически сложно.

Целью данной работы является исследование зависимости достижимой скорости передачи от длительности импульсов с учетом их нелинейного взаимодействия.

Для описания процесса эволюции сверхкоротких импульсов большой интенсивности вдоль волоконного световода принята обычно используемая в таких случаях [1-3] модель в виде нелинейного уравнения Шредингера

1 |^ + |^ + Х1Ф12Ф = О,                                                 (!)

где и, т - безразмерные переменные, связанные с продольной координатой z и реальным временем t через характерные масштабы Lo, То (например, "дисперсионную длину" и начальную полуширину импульса) и групповую скорость v0 соотношениями

/т „ t - z/vp .

П - Z/Lo, Т - То , •

ф(П, т) - нормированная на начальную амплитуду комплексная огибающая оптического сигнала; X - параметр нелинейности, определяемый характеристиками волокна и начальной мощностью импульса.

Уравнение (1) не отражает потерь в световоде, зависимости групповой скорости от интенсивности, дисперсии высших порядков и некоторых других явлений, учет влияния которых на взаимодействие импульсов является задачей дальнейших исследований.

Указанное уравнение решалось численным методом при начальном условии

ф(0,т) = фо(т) = f(T - Дт) + f(T) + Дт) ,                                     (2)

где f(r) - импульс на входе световода, Дт - полуинтервал между соседними импульсами. Рассматривались импульсы двух форм: соответствующие солитонам, т.е.

f (т) = sech(/ ~ T/Ts) и гауссовские, f (т) = ехр(-т2/2тр, где т , т - параметры эквивалентной ширины импульсов. Для сравнения результа-тов эволюции эти параметры выбирались такими, чтобы ширина импульсов обеих форм на уровне половины максимальной интенсивности была одинаковой, что достигается при

Т = Jl   arch/2

g    * х 1п2 Ts'

Возможность различения соседних импульсов при их наложении, разумеется, в известных пределах (до полного слияния ) относительна и зависит от характеристик приемного устройства. В данном исследовании импульсы считались различимыми при условии, что интенсивность сигнала в точке между их центрами не превышает половины пиковой интенсивности.

Численное решение уравнения (1) при начальном условии (2) при разных значениях Дт и Tg позволяет связать предельную дальность передачи ц , при которой еще сохраняется возможность различения импульсов в указанном выше смысле, с полуинтервалом Дт. На рисунке показаны зависимости минимально допустимого полуинтервала Дт^д (на входе) от параметра ширины импульса xg при различных значениях нормированной дальности передачи и и х = 2, построенные на основе ре-

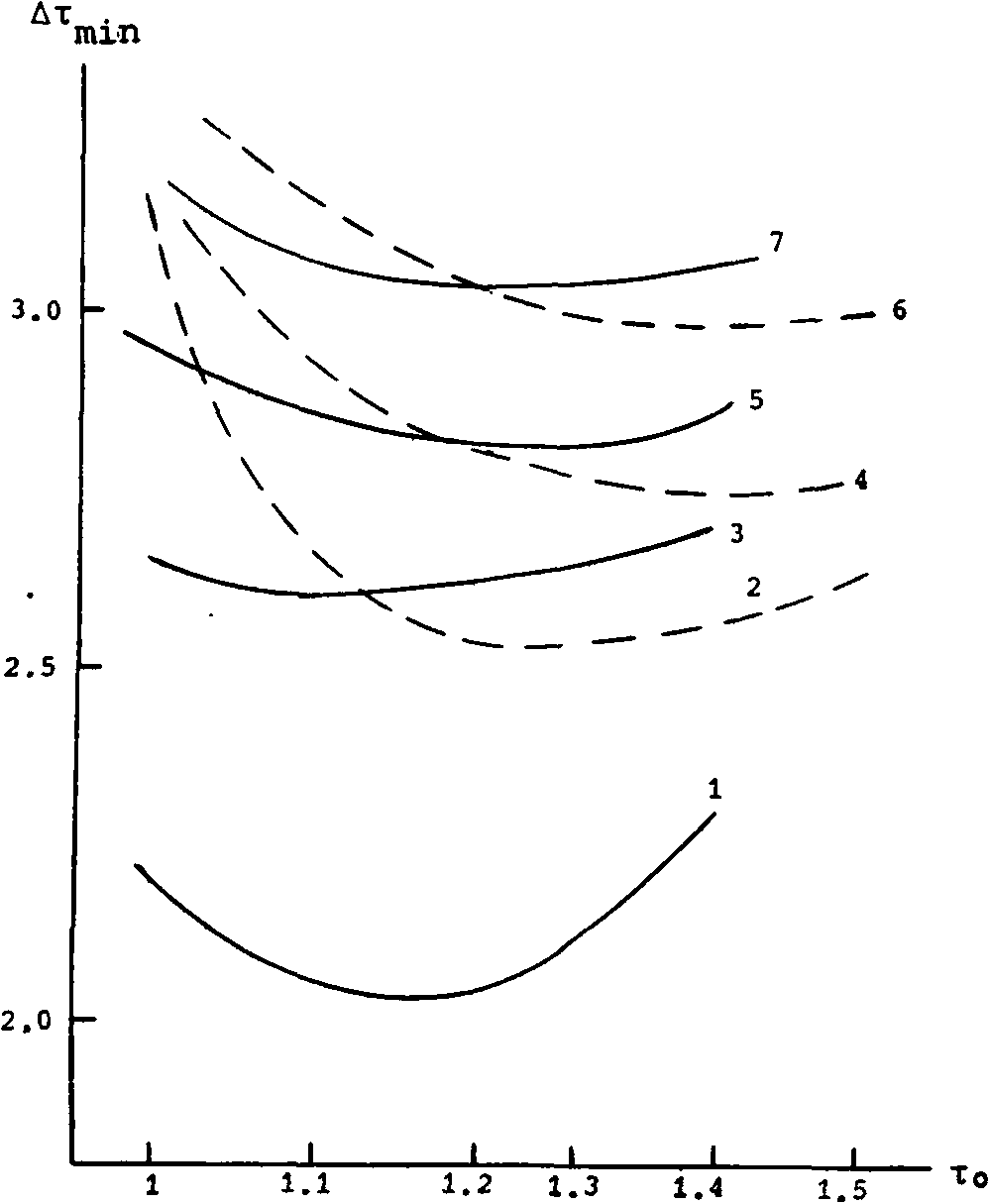
Минимальный интервал между импульсами различной формы в зависимости от начальной длительности при различной дальности передачи: z = 2L₀ (1) , z = 4L_O(2,3), z = 6L_O(4,5), z = 8L_O(6,7) (солитоноподобные импульсы - сплошные линии, гауссовские - штриховые)

зультатов такого исследования. Используя эти графики, нетрудно в каждом случае оценить и предельно достижимую скорость модуляции, определяемую соотношением

V = -------- с-1, max Т° Атш1п с которой при двоичной модуляции совпадает и скорость передачи информации (бит/с).

Детальный анализ результатов моделирования показывает, что нелинейное взаимодействие импульсов в некоторых случаях может заметно ухудшить их разли-чимость по сравнению с простым линейным наложением, поэтому к оценкам предельной скорости передачи, полученным без учета этого фактора, следует относиться с большой осторожностью.

Из полученных графиков видно, что при каждом сочетании значений параметров существует некоторое оптимальное значение начальной ширины импульсов, обеспечивающее наивысшую скорость передачи. Это естественно, так как с сокращением длительности импульсов их различимость на начальном этапе эволюции улучшается, но зато возрастает дисперсия, ухудшающая различимость с увеличением расстояния.

Квазипериодичность, свойственная нелинейным режимам эволюции, приводит к немонотонности зависимости указанных оптимальных значений от длины линии.

Сравнение результатов для импульсов различной формы показывает, что при малых значениях начальной ширины Tg (около единицы) солитоноподобные импульсы обеспечивают передачу с более высокой скоростью, чем гауссовские с той же шириной и мощностью. Однако предельные скорости передачи, соответствующие оптимальным значениям Tg, оказываются наибольшими при использовании импульсов гауссовской формы.