Оптимальная организация экологического мониторинга на базе группы беспилотных летательных аппаратов
Автор: Гулиев Фалах Фахраддин Оглы
Журнал: Научное приборостроение @nauchnoe-priborostroenie
Рубрика: Разное
Статья в выпуске: 4 т.22, 2012 года.
Бесплатный доступ
Результаты информационной оптимизации лазерного канала связи между элементами группы БПЛА, осуществляющиx групповое дистанционное зондирование, показали, что в оптимальном режиме увеличение длины волны оптического сигнала неизбежно приводит к уменьшению достижимого расстояния между БПЛА. Результаты исследования зависимости требуемой площади полезного груза, предназначенной для размещения аппаратуры дистанционного зондирования, показали, что с увеличением длины волны указанная площадь неизбежно увеличивается.
Экологический мониторинг, беспилотные летательные аппараты, оптимизация, дистанционное зондирование, групповой полет
Короткий адрес: https://sciup.org/14264817
IDR: 14264817 | УДК: 623.746;
Текст научной статьи Оптимальная организация экологического мониторинга на базе группы беспилотных летательных аппаратов
Как отмечено в работе [1], дистанционное зондирование с использованием беспилотных летательных аппаратов (БПЛА) является наиболее подходящим техническим решением для менее развитых стран. Использование спутниковых систем проведения локального или регионального мониторинга является практически недосягаемым и слишком дорогим для них, что подчеркивает актуальность разработки высокоэффективных технологий дистанционного зондирования, предусматривающих оптимальное использование ресурсов указанных носителей. В настоящей статье мы проанализируем возможность оптимального выбора основных режимных параметров группы БПЛА, совершающих совместное дистанционное зондирование, и покажем пути эффективного использования геометрического ресурса БПЛА в отдельности.
ПОСТАНОВКА ЗАДАЧИ О ДИСТАНЦИИ МЕЖДУ БПЛА
Проанализируем вопрос об оптимальном выборе длины волны в канале лазерной связи, используемой для организации коммуникации при групповых полетах БПЛА между центральным и периферийным БПЛА (см. рисунок). С этой целью проанализируем достижимую величину отношения сигнал / шум в лазерном оптическом канале при передаче по этому каналу информации спектрального дистанционного зондирования.
Как указано в работе [2], взаимосвязь между мощностью сигнала периферийного БПЛА и мощ- ностью сигнала, принимаемого центральным
БПЛА ( Ргцентр ) , определяется по следующему выражению:
P r центр
= П т • П--
πZ 2
Sη rec η can
t 2 an
(
2πD com
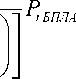
где Srec — площадь апертуры спектральной аппаратуры центрального БПЛА; PtБПЛА — мощность оптического сигнала БПЛА; ηТ — оптическая эффективность передатчика; ηR — оптическая эффективность приемника; Z — расстояние между λ передатчиком и приемником; — угол рас-
π Dcom хождения лазерного луча, обусловленный дифракцией; ηcan — пропускание канала, определяемое как
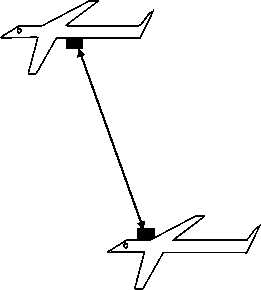
Графическая иллюстрация оптической связи при групповом полете двух БПЛА
η can
e - Z о ( Л )
где о ( Л ) — оптическая плотность канала.
Согласно [2], при
λ
D com
<< 1 имеем
РЕШЕНИЕ СФОРМУЛИРОВАННОЙ ОПТИМИЗАЦИОННОЙ ЗАДАЧИ
Безусловный информационный функционал, подлежащий оптимизации, имеет следующий вид:
f Л
I 2nD J 4п2DD com com
λ max ^ е- ф ( Л )( о о + оЛ ) ^ max
F o = J ln a2 ,2 d Л + Y J ф ( Л ) d Л , (9)
A ni„ ф ( Л ) • Л Л.т
Следовательно, получаем р = к D2 Zo(Л) (2)
1 гцентр ,v2 ^com e , W
где γ — множитель Лагранжа.
Согласно методу Эйлера, решение вышеуказанной оптимизационной задачи определяется по следующему условию:
где
d ( F i + F 2 ) d ф ( Л )
k 2 =
4 ПП Т • nR • Arec • Pt БПЛА Z 2 λ 2
С учетом выражений (9) и (10) получаем следующее уравнение:
Величина фототока в приемнике центрального БПЛА связана с мощностью принятого оптического сигнала следующим образом:
-[( о 0 + о'Л ) • ф(Л ) + 2 ] =
ф ( Л ) . Л2 Y .
центр . БПЛА r центр ,
Из выражения (11) имеем
где R — чувствительность приемника.
С учетом выражений (1)–(4) и разложения
о( Л) = о 0 + о' Л отношение сигнал / шум канала коммуникации определится как
л Р - Z ( о 0 + ОЛ ) SNR ^ = — e-—-- ,
Z 2 λ 2
ф ( Л ) Y . Л 2 + ( о 0 + о Л ) .
С учетом выражений (8) и (12) получим
λ max
Г^d Л = C .
2„ Y • Л - ( о 0 + оЛ )
где
Не останавливаясь подробно на раскрытии определенного интеграла (13), примем условное обозначение
A =
R " Dcom " 4 ПП Т P r " Srec " Р1БПЛА
N 0 B
а N 0 — спектральная плотность шумов, B — ширина полосы частот приемника.
Задача оптимизации ставится следующим образом. Следует вычислить оптимальную функцию Z = ф ( Л ) , которая привела бы интегральный информационный функционал
λ max
F = J ln
λ min
A • e - ф ( Л )( о 0 + оЛ ) ф ( Л ) 2 . Л2
d λ
Y = B ( Л тах, Л т1П, о 0 , 0 ' , C ) = B 0 . (14)
С учетом выражений (11) и (14) получим
Z ■ ф ( Л ) = ! ’Я ,2 „'Г °5)
Л B — о 0 — о Л
Как видно из полученного решения (15) при отрицательной величине о' наблюдается уменьшение Z при увеличении λ . Однако при положительном значении о' можно ждать появления максимума функции ф ( Л ) при значении длины волны
к его максимальному значению при соблюдении следующего ограничительного условия:
о 0 + °' |
2 B
λ max
F 2 = J ф ( Л ) d Л = C . (8)
λ min
Далее в настоящей статье, следуя методике, изложенной в [2], рассмотрим вопрос об оптимальном распределении полезного объема грузового отсека БПЛА с учетом размещения в нем как аппаратуры дистанционного зондирования, так и аппаратуры связи и управления.
РЕШЕНИЕ ЗАДАЧИ ОПТИМИЗАЦИИ ГЕОМЕТРИИ ОБОРУДОВАНИЯ БПЛА
Считаем, что осуществляется групповой полет БПЛА, где центральный БПЛА оборудован прие-мо-передатчиком оптического сигнала. При этом остальные БПЛА могут иметь лазерный трансивер или ретрорефлектор, способный модулировать пучок лазера, посланного с центрального БПЛА. При проектировании таких систем с использованием БПЛА должно быть учтено следующее равенство:
D2 + D2 = D2 , (17) sens com v ar , где Dsens — одномерный размер отсека, где размещаются приборы дистанционного зондирования; Dcom — одномерный размер отсека, где размещается трансивер; Dvar — одномерный размер суммарного приборного отсека, который подлежит определению.
Как указывается в [2], способность оптической аппаратуры к двухмерному зондированию сверху ограничена дифракционным пределом. Согласно критерию Релея по пространственному разрешению, минимальная длина объекта, которая может быть различена оптической системой, определяется как
определяется как
C = B log2 1 + — .
2 1 N )
С учетом выражений (5) и (6) имеем
C = B • log2 <
Г R • k 2 • D om • e 1 +--------------
N 0 B
' ( - ) ] 2 1
----— r - (22)
Известно, что при широкой полосе частот имеет место следующий предельный переход:
lim B • log2 ( 1 +—1^ 1.44 — . (23)
B - 62 V N 0 B ) N 0 V '
Следовательно, имеет место следующее равенство:
k 1 •
( D 2
sens
V
—
λ 2
D com |= 1.44
( R2-k2- —2ZZa ( - )• D4 1
R k 2 e D com
V
N 0
. (24)
)
Из выражения (24) окончательно имеем
D sens = 1.12 ^ - -1- Г Rk 2 • e- Z - ( - ) ^ 2 т 1 . (25)
V k 1 N 0 L J
A l = 1.22 f- , Ф
где λ — длина волны оптического сигнала; f — фокусное расстояние линзы; Ф — диаметр линзы.
Как указывается в работе [1], с учетом вышеуказанных дифракционных ограничений максимальная скорость формирования информации может быть вычислена по следующей формуле:
D 2
R d = k 1 ; ,
V - )
где
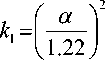
• f • Q ;
Таким образом, как видно из полученного выражения (25), выражение Dsens растет с увеличением λ . Суммируя результаты двух сформулированных решений в данной статье задач, необходимо отметить, что любое увеличение используемой длины волны в канале коммуникации в групповых системах дистанционного зондирования на базе БПЛА приведет к двум негативным последствиям, а именно произойдет:
-
1) уменьшение величины допустимого расстояния между парой БПЛА, связанных лазерным каналом связи;
-
2) увеличение части приборного отсека, необходимой для размещения приборов дистанционного зондирования.
α — угол зрения оптики; F — частота кадров; Q — уровни квантования.
Оценим пропускную способность оптического канала с учетом аэрозольного загрязнения атмосферы. Если в системе действует только аддитивный гауссовский шум, то пропускная способность
ЗАКЛЮЧЕНИЕ
В заключение сформулируем основные выводы и положения проведенного исследования.
-
1. Результаты информационной оптимизации лазерного канала связи между элементами группы БПЛА, осуществляющими групповое дистанционное зондирование, показали, что в оптимальном режиме увеличение длины волны оптического сигнала неизбежно приводит к уменьшению достижимого расстояния между БПЛА.
-
2. Результаты исследования зависимости необ-
ходимой площади, предназначенной для размещения аппаратуры дистанционного зондирования, показали, что с увеличением длины волны указанная площадь неизбежно увеличивается.


