Оптимальная траектория движения позиционного электропривода

При проектировании электропривода одной из главных целей в большинстве случаев является повышение производительности механизма. Однако ограничения, обусловленные возможностями силового, механического и электромеханического оборудования, например, по току, максимальной скорости, нагреву, делают актуальной задачу оптимального управления электроприводом [1–4].

Поэтому синтез силовой части электрооборудования необходимо начинать с поиска оптимальной кривой скорости рабочего органа m(t). Критерием расчета принимался минимум электрических потерь в электроприводе

Q = mi^^Q(i;r), где Q = f^4 I2rdt - активные потери в обмотке. При расчете постоянным принималось значение суммарного угла поворота рабочего органа Ф = f(Мc(t); m(t)) = const. Предполагалось, что переменные электрические потери зависели только от тока и активного сопротивления обмотки, которое не изменяется при нагреве машины.

Методом вариационного исчисления доказывается, что для случая, когда единственным ограничением при проектировании электропривода является ограничение по нагреву, оптимальными являются параболическая диаграмма скорости и линейная диаграмма тока [5]. Однако при учете ограничения по току вид оптимальных диаграмм меняется. В случае, когда

im>^QTr, где 1т - максимальное значение тока, T - время цикла; длина линейного участка оптимальной диа- граммы обращается в ноль. Оптимальной становится прямоугольная форма, при которой ток меняется от +1т до -1т. Диаграмма скорости приобретает «треугольный» вид с изломом в момент времени tп (рис. 1). В этом случае время пуска и торможения равны соответственно:

t = Т + McL п 2 2Im;

_t = Т — М с Т

^T 2 2I_m

Для диаграммы, учитывающей локальное ограничение по току:

Q = imt;

h = —2 /^- M2 = -^-7l2 —М2, 4T2 t c 4T2 m c’ где Q - суммарные потери, h - перемещение исполнительного механизма.

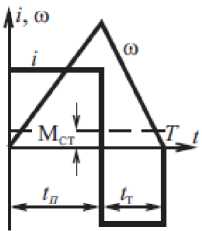
Рис. 1. Оптимальные нагрузочные диаграммы тока и скорости при учете ограничений по нагреву и току

Таким образом, форма нагрузочных диаграмм была определена однозначно. Однако величину участков пуска и торможения следовало уточнить. Оптимальной кривой скорости позиционного электропривода является равнобедренный треугольник или трапеция, т. е. оптимальным является соотношение времени разгона к времени торможения 1:1 [6]. Между тем оптимальным соотношением времени разгона к времени торможения является 2:1. Оптимизируется данное соотношение по критерию минимума потребляемого из сети тока при максимальном перемещении.

В силу отсутствия обоснования оптимального соотношения времени разгона ко времени торможения выскажем ряд гипотез, объясняющих это утверждение [7]. Предположим, что на положение оптимума влияет наличие люфта. Тогда при том же графике скорости двигателя, что и в случае идеальной системы, труба переместится на меньшее расстояние. Будем сдвигать во времени сигнал на торможение, увеличивая тем самым время разгона (рис. 2). Критерием оптимизации является отношение среднеквадратичного момента двигателя за время позиционирования к перемещению трубы M ср.кв / s , где

Мср.кв= I^J^М(t))2 dt.

\ Тл.л

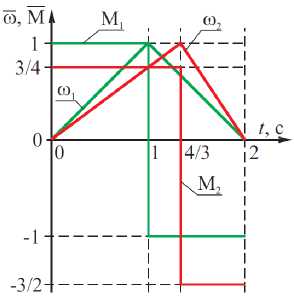
Рис. 2. Пояснение к расчету М _ср.кв / s

Тогда при постоянстве модуля ускорения на всем времени переходного процесса

МРРРВРР = 7 М2^ + МТ t т =

= V1271T127T = V2.

Принимаем, что разгон осуществляется до со = 1, время пуска t_л = 1 с, время торможения t _T = 1 с. Во втором случае, например, когда время пуска t_л = 4/3 с, время торможения t _T = 2/3 с, т. е. сумма t_л + t _T также равна 2 с:

Ki Р =    2t   M2t = ср.кв.2         л^л + т^т

2             2

= 1(9 1+(Э 14

Перемещение s трубы в системе с бесконечной жесткостью винта С , которую в общем случае можно считать одномассовой, будет равно

5 = /о™ ®i(t)dt.

В случае идеально быстродействующего контура момента график скорости во времени будет иметь треугольную форму. Тогда перемещение можно рассчитать как площадь данного треугольника. Очевидно, что она не будет зависеть от доли времени разгона, так как

• 5 = 1ГП псо = ^2Л = 1. 2 л.л 2

При наличии люфта, равного в пределе 1/8 s , перемещение в обоих случаях будет равно 5 1 = = 5 2 = 7/8.

Сравнивая два данных случая, можно убедиться, что

М с ^р .кв.1 <  М ср . КВ.2 . $ 1            $ 2

Далее была выдвинута гипотеза о том, что оптимальная доля времени разгона зависит от жесткости винта. Тогда график скорости будет иметь криволинейный характер. Перемещение трубы можно рассчитать как

5 = 1оТлЛ to2(t)dt, где ю2 - приведенная угловая скорость трубы.

Обе гипотезы проверялись на математической модели в пакете Matlab [8]. Электропривод был представлен в виде двухмассовой модели. Справедливость такого математического описания доказывается методом декомпозиции. На рис. 3 и 4 приведены результаты исследований [9]. Из графиков становится понятным, что при любой упругости винта и наличии максимально возможного люфта оптимальным остается соотношение t _л : t _p = 1:1. Кроме того, на рис. 4 можно заметить, что при значительном уменьшении жесткости винта система становится чрезмерно податливой, и при том же моменте перемещение трубы будет стремиться к нулю, как и показатель М /5. При увеличении жесткости выше С = 120 показатель М /5 = сonst, и система в этом случае вырождается в одномассовую [10–12]. Однако данные исследования проводились при М с = 0 и не учитывают реального характера нагрузки.

Позиционный электропривод подачи, работающий на участке разгона, преодолевает момент сопротивления, создаваемый перемещаемой трубой, а на участке торможения к этому моменту добавляется усилие, обусловленное влиянием главного привода. Наилучшее использование электропривода по нагреву идет при постоянном графике электромагнитного момента и при изменяющейся во времени кривой момента сопротивления, динамический момент на участке торможения существенно превышает момент на участке разгона электропривода.

Очевидно, что при попадании трубы в валки на последнем этапе позиционирования изменяется вид графика момента сопротивления во времени с постоянного на ступенчатообразный. Это обстоятельство заставляет задуматься о необходимости

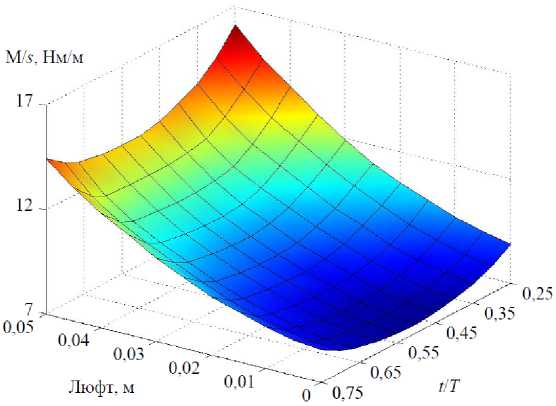
Рис. 3. Зависимость отношения момента двигателя М к перемещению трубы s от люфта и доли времени разгона в общем времени позиционирования

Рис. 4. Зависимость отношения момента двигателя М к перемещению трубы s от жесткости винта С и доли времени разгона в общем времени позиционирования

оптимизации доли времени разгона во времени всего переходного процесса [13].

Данная задача в вариационном исчислении относится к классу изопериметрических. Расчет оптимальной формы кривой скорости выполнялся методом наискорейшего спуска, который представляет собой усовершенствованный градиентный метод. Его отличительной особенностью его является отсутствие необходимости частого вычисления производной от исследуемой функции за счет применения переменного шага H поиска экстремума по направлению. Классический градиентный метод требует вычисления градиента с постоянным шагом [14]. Таким образом, применение метода наискорейшего спуска вдали от оптимума дает значительный эффект, поиск оптимума производится гораздо быстрее. В окрестностях точки экстремума время его поиска обоими методами практически совпадает.

Алгоритм поиска минимума функции потерь Q при фиксированной форме нагрузочных диаграмм состоял из следующих этапов.

В начальной точке определялся градиент

SO = VQ = f^,

Otn где Q = f(tn~). Далее вычислялись координаты следующей точки:

• ^t ni = ^t no + HS o .

В данном случае величина шага H была переменной и при каждом цикле расчета уточнялась из условия

Fk(Hk) = minH>o Fk(H), где Fk(H) =f[tnk)-Hf'(tnk))].

Величина же скачка, обусловленного попаданием трубы в валки прокатной клети, может варьироваться, что в существенной мере повлияет на среднеквадратичный момент двигателя за время переходного процесса и в конечном итоге на его нагрев [15]. На рис. 5 представлена зависимость значения оптимального времени пуска t _п/ t _ц от момента наброса нагрузки t_{М с} и амплитуды момента сопротивления А_{М с}. Как и ожидалось, при отсутствии неравномерности момента ( А_{М с} = 0) оптимальным соотношением является 0,5. При увеличении А М с оптимум сдвигается в сторону увеличения. На рис. 6 показана зависимость отношения среднеквадратичного момента при оптимальной траектории к моменту при равенстве участков пуска и торможения от времени и амплитуды скачка момента нагрузки, обусловленного попаданием трубы в валки клети.

Осциллограммы скорости, полученные на работающем объекте, были обработаны статистически. Поскольку реальной возможности зафиксиро- вать изменение момента сопротивления не было, точка срыва трубы определялась косвенно по диаграмме скорости [16]. Таким образом, удалось определить среднестатистическое время наброса нагрузки, обусловленное попаданием трубы в валки. Учитывая, что квантиль Стьюдента получился tC < 2,26 для выборки из 10 экспериментов, с вероятностью 95 % можно утверждать, что момент срыва трубы с оправки будет составлять 0,67tц. Доверительный интервал для данной выборки будет составлять 0,07. Тогда на основании статистической обработки можно утверждать, что время дискретного увеличения момента нагрузки будет лежать в диапазоне (0,6…0,74)tц (см. таблицу) [17]. Вертикальными границами на рис. 6 обозначена область предполагаемого времени наброса нагрузки. Полученная выгода в среднеквадратичном моменте считалась для оптимального соотношения времени tп/tт в сравнении со среднеквадратичным моментом, полученным для соотношения tп/tт = 1:1. Известно, что мощность активных потерь в элек-

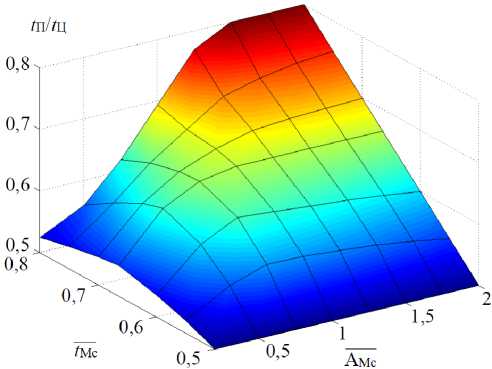
Рис. 5. Оптимальное соотношение t _п / t _ц в зависимости от момента срыва трубы с оправки t_{М с} и амплитуды момента сопротивления A_{М с}

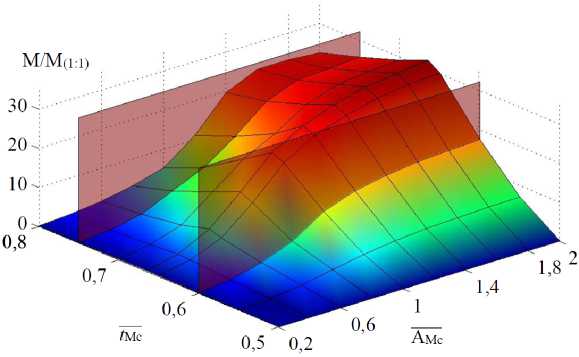
Рис. 6. Зависимость отношения среднеквадратичного момента М _ср.кв при оптимальной траектории к моменту при равенстве участков пуска и торможения от времени t_{М с} и амплитуды А_{М с} скачка момента нагрузки

Статистическая обработка времени наброса нагрузки

Номер эксперимента tц tц.ср d d2 1 0,6 0,67 –0,07 0,0049 2 0,65 0,67 –0,02 0,0004 3 0,68 0,67 0,01 0,0001 4 0,62 0,67 –0,05 0,0025 10 0,73 0,67 0,06 0,0036 U2-^2 S^ = A  n-i 0,07 d- ^d t = Sd Vn 2,13 ^крит 2,26 Sd. E = t-d Vn 0,6< 0,67 <0,74 троприводе определяется как Р = /2т. Приближенно можно считать, что Р ~ М2т. Тогда снижаться данные потери будут пропорционально квадрату от выгоды в моменте.

С учетом неравномерного характера нагрузки по критерию минимума М ср.кв / s оптимальное соотношение времени пуска к времени торможения электропривода может варьироваться [18–20]. Рекомендуемым соотношением, исходя из зависимости, представленной на рис. 6 для электропривода подачи стана ХПТ-450, является 2:1.