Оптимальное демпфирование колебаний твердого тела при его движении вокруг неподвижной точки

дого тела в окрестности статически устойчивого положения равновесия, то есть при малых углах нутации, эти уравнения удобно записать в комплексной форме. Тогда, используя результаты работы [3], получим

^ - iJ z « z ^ + a 2 £ =

= eF (r, %,%, az, ф) + eu,(1)

6)z = ef (r, £ az, Ф),

Ф = az + eR (§, ^), где § = 0e11^ - комплексный угол нутации, r -вектор медленно изменяющихся переменных, a2 = AzG/ J, J = (Jx + Jy)/2; Ax, Ay,Az - проекции вектора Ar, определяющего положение центра масс тела относительно неподвижной точки, на оси связанной системы координат; Jx, Jy, Jz - осевые моменты инерции тела; Jz = Jz/J; G - сила тяжести, Ф = ф + ф ; eF (r, ^, t®z, Ф), e f (r,^, az, Ф), eR(^,^) - функции, характеризующие действие малых возмущений; 0,ф,^ -классические углы Эйлера (нутации, собственного вращения и прецессии); az - угловая скорость вращения тела вокруг его продольной оси z ; s и - управление, e - малый параметр.

Невозмущенное движение тела описывается следующими уравнениями

- iJz_a_zi; + ® ² ^ = ,     ⁽⁴⁾

Ф = a _z , a z = const , r = const .   (5)

Решение невозмущенного уравнения (4) можно записать в виде

^ = a 1 e ^ i + a 2 e '"

,

где a ₁ и a ₂ – амплитуды колебаний (вещественные величины), ^ 1 = to t + V 1 (0) и

V 2 = to 1 + V 2 (0) — фазы; ^ 1 (0), ^ 2 (0) — начальные значения фаз; & 1 2 = J z to z /2 ± to g - частоты колебаний; to g = д/ j Z2 ® 2 /4 + to ² .

Резонансные случаи движения твердого тела, когда угловая скорость to z ® to 1,2 в данной работе не рассматриваются, так как требуют особого анализа.

Дифференцируя функцию (6) по времени в силу невозмущенной системы, получим

^ = i ( a 1 to 1 C^{l i}^1 + a 2 to 2 e '"' ² ) .         (7)

Рассматривая соотношения (6) и (7) как замену переменных ( £ , d d / dt ) ^ ( a 1 , a ₂, V 1 , V 2 ) и применяя метод вариации произвольных постоянных, получим стандартную систему с быстрыми фазами [3]

a = E X ( u , a , ф , r ) ,             (8)

ф = to ( r ) + e Y ( u , a , ф , r ) ,           (9)

где a = ( a 1 ,a ₂ ) , ф = ( щ 1, у ₂ ) .

С учетом вышесказанного ставится задача определения управления E u , обеспечивающего динамическую устойчивость движения твердого тела вокруг неподвижной точки исходя из минимума квадратичного критерия оптимальности T

I = e J W ( a_b a 2 , u _a , u p ) dt ,       (10)

где

W = b 1 a ² + b₂a 2 + c ( u a + u p ) , b b ^b 2, ^c >  ^{0 - ве} совые коэффициенты, u = u p + iu _a . Причем амплитуды колебаний определяются в силу возмущенной системы и должны удовлетворять условиям динамической устойчивости a 1 , a 2 <  0 в каждый момент времени.

Движение твердого тела рассматривается на асимптотически большом промежутке времени T = L / E , где L < да - некоторая константа, поэтому функционал (10) изменяется на величину порядка O ( 1 ) .

Согласно принципу динамического программирования, оптимальное управление определяется из условия [1]

. (е V . д V ; д V . min I a + ф + r + u _a , u p (д a      дф     д r

+ W ( a , u _a , u p ) ) = 0 ,             (11)

где V ( a, ф , r ) - производящая функция [1], а точка ( • ) означает скалярное произведение векторов.

Выражение, стоящее под знаком минимума (11), представляет собой квадратичный степенной полином по компонентам управления u _a , u p . Поэтому, взяв от этого выражения частные производные по u _a , u p и приравняв их к нулю, нетрудно получить оптимальное управление в виде

/

u _a

n k д V

. Z (^{- 1} ) —cos V k ^{4 c to}g k =1        ^я-

(

^{д a} k

1 д V uo =

^a k ^д ^ к

T¹- ^Z ( - 1 ) 4 c to g k = 1

1 д V k+1 д V .

I  — sW k ⁺

( ^{д a} k

+ —-— cos V k I. ^a k ^k     )

Выражения (12-13) обеспечивают минимум функционала (10) в силу положительной определенности функции W (ab a2, ua, up) и при надлежащем определении производящей функции V . Подставив соотношения (12-13) в выражение (11) приходим к уравнению в частных производных Гамильтона – Якоби – Беллмана где

д V

• X0 (a ,ф,r) +       • Y0 (a,ф,r) + д a д V    , x   д V  .     2.

+^ ^to ( r ) ■ _r • r ⁺ e Z b k a k + U = 0, (14)

• дф         д r

• X ₀, Y ₀ – часть функций X , Y , не зависящая от

  управления, U = -e c

  
  

  , r = O ( e ) , а ^ a

  
  

и u^op определяются выражениями (12-13).

Для решения уравнения (14) применяется метод усреднения. После проведения операции усреднения уравнения (14) по фазам получим д Уа2

—0 •(X0 (a,ф, r)) + e Z bkak + д a

+ (U> + O (e 2) +... = 0,(15)

где 0 - стандартный оператор усреднения фазам, V0 = V), по

16 c to g

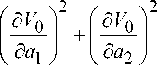
Пусть положительно определенная функция

V0 (a) есть решение, удовлетворяющее уравнению первого приближения (15). Ее полная производная по времени, определенная в силу усредненной системы первого приближения, будет равна

• ^V 0 = ^- W ( ^a , u a , ^uO p )) . (16)

Учитывая вид функции W(a,ua,up) (10) ее усредненный аналог W(a,u

Рассматривается действие линейных возмущающих функций вида s F (г, Е, Е) = s (i^zmz^ + Ц*), где Mz и ц - некоторые заданные коэффициенты, которые могут зависеть от вектора ^r .

Усреднение функций X₀(а,ф,г), входящих в уравнение первого приближения (16) дает

рассчитанный по исходной нелинейной модели движения твердого тела.

В работе была изложена методика расчета приближенно оптимальных регуляторов, предназначенных для стабилизации движения твердого тела вокруг неподвижной точки (волчок Лагранжа). Показано, что при наличии малых линейных возмущений существует аналитическое решение поставленной задачи.

(X0 (а ,ф, г

где v12 = ±Mz^z ± ц®^, Mz и ц - параметры, характеризующие действующие возмущения.

Решение уравнения (15) в этом случае нетрудно найти, используя метод неопределенных коэффициентов. Тогда, определяя решение в виде 2

V0 = I Bkak , подставляя его в (15) и приравнивая =1                               2     „2

к нулю коэффициенты при a₁ и a₂ , получим

Рис. 1. Процесс демпфирования колебаний

B_k = 2®_еc^vk +

4 +

k ,

на плоскости

где k = 1,2.           ^{L                   J}

Тогда функции оптимального управления (12-13) примут вид

(g^g*)

ua

/

k.k[aV . I (^-1) ^cos^k ⁴ctog k=1

^^^^^^s

^^^^^^s

s d V

V

aak

u°p =

ak ^dVk

T¹- I (-1) 4 to k=1

. k+1 ^[d V .

I    T-° sin^k⁺

V^dak

s d V         |

+—^cos^k I.

ak ^dVk      J

После подстановки оптимального управления (19-20) в уравнения для амплитуд и усреднения по фазам, получим в первом приближении метода усреднения

.       ^sa12 n : T"

^at1,2 =^-^,    V^v1,2 ^{+ b}1,2/ c .           (21)

2юд

Вид уравнения (21) подтверждает динамическую устойчивость da1 2 / dt< 0 движения твердого тела при действии возмущений.

В качестве примера расчета оптимального регулятора рассматривается случай демпфирования колебаний твердого тела при следующих исходных данных:

to = 0.8c"1, to_z (0) = 1 c"1, J_z = 0.8, 0(0) = n/2, ц = 0.05, M_z = 0.01, b1 = b₂ = 1, c = 100.

На рис. 1 показан процесс демпфирования нутационных колебаний с помощью определенного приближенно оптимального регулятора,

Хотя выше рассматривается движение твердого тела в нерезонансных областях, однако предлагаемый метод управления может быть полезен для уменьшения влияния резонансов на движение системы. При пересечении резонансных областей ®_z ~ to,2 система может вести по-разному. Особенно опасна реализация длительных резонансных режимов движения твердого тела (захватов в резонанс), когда резонансные отношения частот поддерживаются длительное время в силу действующих возмущений. В этом случае, как правило, происходит существенное увеличение значений амплитуд колебаний по углу нутации, что недопустимо в прикладных задачах. Во многих работах (например, [4], [5]), посвященных изучению резонансных эффектов при движении твердого тела в случае Лагранжа, показано, что поведение системы в резонансных областях to_z - to,2 в существенной степени зависит от вида пространственного движения тела, который реализуется при подходе к резонансной области. Пусть, например, при приближении к резонансной области имеем to_z > 0, тогда осуществляется проход через резонанс to_z - ®1, и устойчивость резонансного режима движения определяется изменением амплитуды a₁. В общем случае реализация захвата в резонанс имеет вероятностный характер (случайными являются значения фаз и других характеристики движения тела при пересечении резонанса). Однако, если значения амплитуды a₁ малы, то достаточные условия устойчивости резонанса, как правило, не

выполняются, и реализация захватов в резонанс маловероятно. Отсюда следует очевидный вывод, что если тело близкое к телу вращения имеет специально созданную закрутку в положительном направлении toz > 0, регулятор надо строить так, чтобы осуществлялось приоритетное демпфирование амплитуды a₁, что можно обеспечить в рамках рассматриваемой постановки задачи, увеличивая весовой коэффициент b₁ в критерии оптимальности (10). С точки зрения описания движения в исходных переменных при подходе к резонансной области необходимо реализовать случай так называемой обратной прецессии твердого тела, когда toz > 0 и dy / dt < 0. Аналогично, если toz < 0, то необходимо уменьшить амплитуду a2, чтобы обеспечить dy / dt > 0.