Оптимальное квантование в задаче компрессии цифровых сигналов

Характерной чертой многих современных прикладных задач обработки информации (хранение космических снимков, передача видео и звука через Интернет и так далее) является работа с большими объемами данных. В таких условиях особенно актуальной становится задача компрессии цифровых сигналов.

Работа многих известных алгоритмов компрессии сигналов и изображений (JPEG [1], ДИКМ [2] и другие) в целом может быть описана структурной схемой, изображенной на рис. 1.

Рис. 1. Структурная схема работы алгоритмов компрессии.

Сначала исходные данные подвергаются некоторому обратимому декоррелирующему преобразованию. Преобразование выбирается таким образом, что в результате него компоненты преобразованного сигнала имеют меньшую дисперсию и за счет этого обладают меньшей статистической избыточностью. В алгоритме JPEG для этого используется косинусное преобразование [2], а в алгоритме ДИКМ вычисляется разностный сигнал, который получается вычитанием предсказанного значения сигнала из исходного. Затем преобразованный сигнал квантуется в соответствии с некоторой шкалой квантования. После этого квантованный сигнал подвергается статистическому кодированию [3]. На этом этапе и происходит собственно сокращение объема данных.

При квантовании в сигнал намеренно вносится некоторая погрешность. Это делается для того, чтобы за счет допустимой потери точности представле- ния исходных данных повысить коэффициент сжатия. При этом чем большая погрешность вносится, тем больше коэффициент сжатия. В свою очередь допустимая погрешность определяется спецификой решаемой задачи и обычно не может быть больше некоторой, наперед заданной величины. Другими словами, на практике часто необходима возможность контроля (управления) погрешностью. Таким образом, основными требованиями к шкале квантования являются минимизация объема сжатых данных при управляемой погрешности.

1. Постановка задачи построения оптимальной шкалы квантования

В данной работе рассмотрено квантование только целочисленных величин (при необходимости все построения легко обобщаются на непрерывный случай). В формализованном изложении процедура квантования дискретной целочисленной величины x , принимающей значения на диапазоне [ L , R ] , заключается в следующем. Диапазон [ L , R ] разбивается на ( N - 1) интервал квантования:

N - 2

[ L , R ] = J ( b j , b j + 1 ], j = 0

b j ^G Z ^{, b} 0 = L — 1, ^b N - 1 = R .

Затем на каждом интервале  квантова ния (bj, bj+i] выбирается представительное значе ние cj , то есть задается вектор c = {Cj gZ: bj < Cj < bj+1, j g [0, N - 2]}.

Собственно квантование заключается в том, что значение величины x заменяется на представительное значение c_j того интервала квантования ( b j , b j ₊ 1 ], в который попадает x . Как будет показано ниже, для всех рассматриваемых шкал существует способ расчета представительных значений c_j через значения границ b_j интервалов квантования. Другими словами, определена функция C ( b j , b j ₊ 1 ), которая для любого интервала квантования ( b j , b j _{+ 1}] вычисляет его представительное значение:

C j = C ( b j , b j + 1 )                                   (1)

Таким образом, можно считать, что шкала квантования однозначно определяется N - мерным вектором b границ интервалов квантования:

b = { b j gZ : b j < b j + 1 ,b 0 = L - 1, b N - 1 = R , j g [ 0, N ) }

Как уже было отмечено выше, требованием к оптимальной шкале квантования является миними- зация объема сжатых данных при управляемой погрешности. Известно, что при использовании достаточно хороших алгоритмов статистического кодирования объем сжатых данных приближается к энтропии кодируемых величин. Это позволяет заменить критерий минимизации объема сжатых данных на более простой критерий минимизации энтропии величины x после квантования.

Пусть f ( x ) - распределение вероятностей величины x . Тогда вероятность попадания величины x в любой интервал квантования ( l , r ] может быть записана в виде:

r

P ( l , r ) = X f ( x ).

x = l + 1

Во введенных обозначениях можно записать выражение для энтропии величины x после квантования:

N - 2

H 2 ( b ) = - X P ( b j , b j + i )log 2 P ( b j , b j + 1 )

j = 0

и критерий минимизации этой энтропии:

H 2 ( b ) ^ min .                            (2)

b

Также было отмечено, что ограничением при минимизации этого показателя качества является требование управляемости погрешности. В качестве погрешности будем рассматривать среднеквадратичную ошибку (СКО), привносимую при квантовании. Везде далее для удобства будет использоваться квадрат этой величины – дисперсия ошибки:

N -2 /       \ s2(b) = Xs2 (bj, bj+i), j=0

где s ² ( l , r ) - погрешность, привносимая на интервале квантования ( l , r ] :

r s2( l, r) = X(x - C (l, r) )2 f (x).

x = l + 1

Во введенных обозначениях требование управляемости погрешности может быть записано следующим образом:

• ^s2 ^(b)^Smax,                                ⁽³⁾

2.    Шкалы квантования

где s _max - наперед заданное наибольшее значение погрешности, допустимое при квантовании.

Критерий (2) с ограничением (3) определяет формальную постановку задачи поиска оптимальной шкалы квантования в задаче компрессии цифрового сигнала.

В настоящее время известно множество различных шкал квантования, построенных исходя из специфики решаемых задач. Наибольшую извест- ность получили равномерная шкала квантования и шкала Макса [2].

Равномерная шкала строится, исходя из критерия максимальной ошибки, при котором допускает ся отклонение квантованного значения величины x от исходного значения величины x не более, чем на заранее заданную величину. У равномерной шкалы все интервалы квантования имеют одинаковый размер, а представительные значения располагаются по центрам интервалов квантования.

Достоинство такой шкалы состоит в том, что при ее использовании восстановленный сигнал в каждой точке отличается от исходного не более чем на заранее заданную величину, равную половине размера интервала квантования. В свою очередь это дает возможность переборным способом найти равномерную шкалу, удовлетворяющую заданному ограничению по СКО. Недостатком шкалы является то, что требование минимизации энтропии при этом не учитывается.

Шкала Макса строится, исходя из критерия минимума СКО при фиксированном количестве ( N - 1) - интервалов квантования. Итерационный алгоритм построения такой шкалы описан в [2]. Единственным управляющим параметром такой шкалы является параметр N , подбирая который, можно построить шкалу, удовлетворяющую заданному ограничению по СКО. Однако так же, как и в случае равномерной шкалы, требование минимизации энтропии при этом не учитывается.

Рассматривая свойства этих шкал, можно сделать вывод о том, что они не дают решения задачи, сформулированной выше. Таким образом, возникает необходимость отыскания шкалы квантования, удовлетворяющей предъявленным требованиям.

3.    Алгоритм построения оптимальной шкалы квантования

Поставленная задача не решается аналитически в силу своей нелинейности и является по сути переборной. Однако сложность полного перебора настолько велика (необходимо рассмотреть C^N - l различных шкал), что не позволяет рассчитывать на получение результата за сколько-либо приемлемое время. Поэтому был разработан квазиоптимальный алгоритм, позволяющий сократить перебор до допустимых пределов за счет некоторой потери оптимальности.

Основная идея алгоритма, заимствованная из динамического программирования [4], заключается в следующем. Если из оптимальной шкалы удалить последний интервал квантования, то оставшаяся подшкала также будет оптимальна при “своей” погрешности, равной полной погрешности за вычетом погрешности, привносимой на последнем интервале квантования. Этот факт позволяет строить оптимальную шкалу, последовательно наращивая количество уровней.

Опишем подробнее идею алгоритма. Введем в рассмотрение уменьшенный диапазон значений кван- 2

туемой величины [ L , r ] и допустимое СКО e max . На этом диапазоне легко строится оптимальная шкала, состоящая из двух интервалов квантования с границами интервалов квантования b 0 , b 1 , b 2 Действительно, первая и последняя границы известны: b о = L - 1, b 2 = r , а положение средней границы b можно найти простым перебором в диапазоне [ L , r - 1]. Таким образом можно построить оптимальные шкалы из двух интервалов квантования для всех возможных диапазонов [ L , r ] и всех возможных 2

погрешностей e max , а получающиеся значения энтропии и средней границы запомнить в памяти ЭВМ.

Затем аналогичным образом можно поставить задачу поиска оптимальной шкалы квантования из трех интервалов квантования с границами интервалов квантования b 0 , b 1 , b 2 , b 3 на диапазоне [ L , r ] с 2

заданной допустимой СКО e max . Положение первой и последней границ по прежнему известно: b о = L - 1, b 2 = r , а положение предпоследней границы b ₂ будем искать перебором на диапазоне [ L + 1, r - 1]. При этом при проведении перебора для каждого положения предпоследней границы b ₂ необходимо найти оптимальное положение второй границы b на диапазоне [ L , b 2 - 1]. Другими словами, для каждого положения предпоследней границы b ₂ нужно построить оптимальную шкалу из двух интервалов квантования на диапазоне [ L , b ₂ ] , причем допустимая СКО для этой шкалы известна и 22

равна полному СКО e max за вычетом e ( b 2 , r ) - погрешности на интервале квантования ( b ₂, r ] . Так как эта задача была решена на предыдущем шаге, то для каждого положения предпоследней границы b ₂ можно сразу указать положение второй границы b ₁ . Следовательно, в результате перебора по b ₂ на диапазоне [ L + 1, r - 1] будет построена искомая оптимальная шкала из трех интервалов квантования. Так строятся оптимальные шкалы из трех интервалов квантования для всех возможных диапазонов [ L , r ] 2

и всех возможных погрешностей e max .

Затем аналогичным образом строятся все шкалы из четырех интервалов квантования и так далее. На каждом шаге при поиске предпоследней границы используются оптимальные шкалы предыдущего шага, содержащие на один интервал квантования меньше. Запишем разработанный алгоритм формально.

Сначала необходимо описать способ расчета представительных значений интервалов квантования, то есть задать функцию C(l, r) (1). Так как величина энтропии шкалы однозначно определяется положением границ интервалов квантования и не зависит от значений представительных уровней, то значения представительных уровней следует выбирать, исходя из минимизации СКО. В [2] показано, что, при фиксированных значениях границ интервалов квантования, минимум СКО достигается, если представительное значение на каждом интервале квантования (l, r] совпадает с локальным средним этого интервала квантования:

rr

C ⁽ l , r ) = z xf ( x)   z f ( x ).

x = l + 1        / x = l + 1

Будем считать, что при работе алгоритма диа- 2 пазон рассматриваемых погрешностей [о.. e ²_max ] разбивается на K интервалов величины А е =e max/ ( K - 1). Задавая K или A_e , можно управлять точностью работы алгоритма. Кроме того, при работе алгоритма строятся два набора матриц:

B ⁽ j ) = 1 B j : r ^e [ L + j , R ], ^{k e} [°, ^K ) } , j ^e [1, R - L ), H ⁽ j ) = 1 H j : r ^e [ L + j , R ], k e [°, K ) } , j e [1, R - L ), где j - номер шага. В эти матрицы записываются значения предпоследних границ и энтропии, получающиеся на соответствующем шаге.

Шаг 1

На первом шаге строятся оптимальные шкалы, состоящие из двух интервалов квантования, на всех диапазонах [ L , r ] и для всех максимальных погрешностей k A_e , где r e [ L + 1, R ] и k e [°, K - 1] - варьируемые параметры. Очевидно, что все такие шкалы будут задаваться тремя границами интервалов квантования, из которых первая и последняя известны и равны L - 1 и г соответственно, а средняя не известна. Обозначив эту неизвестную границу за d , энтропию и погрешность любой шкалы из двух интервалов квантования можно записать в виде:

H ⁽¹⁾ ( r , d ) = - P ( L , d ) log 2 P ( L , d ) - P ( d , r ) log 2 P ( d , r ) e 2 ( r , d ) = e ²( L , d ) + e ²( d , r ).

Тогда для каждой правой границы r и каждой допустимой погрешности k A_e оптимальное значение средней границы d может быть найдено простым перебором на диапазоне [ L , r ) . Затем это оптимальное значение заносится в соответствующий элемент матрицы B ⁽¹⁾ , а получающаяся при этом энтропия – в (1) соответствующий элемент матрицы H ^{( )} :

H (1) = min H ⁽¹⁾( r , d ): e ²( r , d ) <  k A J, r ’ k L <  d <  r^{V                                J}

B (1) = arg min { H ⁽¹⁾ ( r , d ): e 2 ( r , d ) <  k A_e } .

r ’ ^k         L <  d <  r                                 ’

Очевидно, что при некоторых значениях параметров может не существовать такого значения средней границы d, при котором выполняется ограничение на погрешность. Здесь и далее в этом случае в соответствующие элементы матриц заносятся специальные значения, указывающие на отсутствии решения.

Шаг j

На j- шаге находятся положение предпоследней границы и энтропия шкал, оптимальных на диапазоне [ L , r ] с погрешностью k A₆ , состоящих из ( j + 1)-интервала квантования. Точно так же, как и на шаге 1, первая и последняя границы известны и равны L - 1 и r соответственно. Обозначим искомую предпоследнюю границу за d и будем искать ее перебором на диапазоне [ L + j - 1, r ).

Для каждого положения границы d слева от d остается шкала из j интервалов квантования, оптимальная на диапазоне [ L , d ] с погрешностью, 2

не превышающей k А_е-е ( d , r ). Энтропия такой шкалы известна, так как была вычислена на предыдущем шаге. Этот факт дает возможность записать энтропию любой шкалы из ( j + 1)-интервала квантования, которая обеспечивает погрешность не более чем k А_е на диапазоне [ L , r ] и содержит подшкалу из j -интервалов квантования, оптимальную на диапазоне [ L , d ] с погрешностью, не превышающей k А_е-е 2 ( d , r ):

H ⁽ j ) ( r , k , d ) = H j¹ - P ( d , r ) log 2 P ( d , r ), (4) где t = [( k A_e-s ²( d , r ) )/a₆ ] .        (5)

Одна из таких шкал обязательно будет являться оптимальной и может быть найдена перебором по d . Построенное таким способом оптимальное значение искомой предпоследней границы заносится в соответствующий элемент матрицы B ^{( j )} , а получающаяся при этом энтропия – в соответствующий элемент матрицы H ^{( j )} :

H ({) = min H ⁽ j ) ( r , k , d )

• ^{r , k} L <  d <  r

B ( j ) = arg min H ⁽ j ) ( r , k , d )

• r ^{, k}        L <  d <  r

Легко видеть, что всего можно сделать R - L - 1 шаг. После того как сделаны все эти шаги, может быть определен номер S -шага, на котором будет построена предпоследняя граница оптимальной шкалы и рассчитана сама шкала.

Обратный ход – собственно построение шкалы

Так как энтропия оптимальной шкалы из ( j + 1 )-интервала квантования равна H RK - 1 , для S можно записать следующее выражение:

^s = arg min H RjK - 1 .

• 0 < j <  R - L

Собственно построение шкалы производится в обратном порядке: от интервалов квантования с большим номером к интервалам с меньшим номером. Легко видеть, что число границ интервалов квантования оптимальной шкалы можно найти следующим образом:

N = S + 2,

предпоследнюю границу можно найти так:

bN-2 = BRNC-21 , а положение каждой следующей границы определяется через положение предыдущей границы:

bj = BVJ,^, где v = bj+1,(6)

w =

N-2/ ejmax - £e2(b,bi+1) /AS

I        i=j+1

4.    Модификация алгоритма

Рассматривая свойства найденных таким образом шкал, можно утверждать, что они будут оптимальными по построению при некотором, достаточно малом A_e . Однако на практике чрезмерное уменьшение А_е приводит к резкому возрастанию времени расчета и необходимого объема оперативной памяти, поэтому реально получаемые шкалы всегда будут квазиоптимальными. Потеря оптимальности происходит из-за того, что на каждом шаге используется шкала предыдущего шага, оптимальная не для заданной погрешности, а для некоторой другой погрешности, которая в худшем случае может быть меньше заданной на j А_е , где j -номер шага. Отметим два следствия этого факта: 1) на каждом шаге может использоваться не оптимальная предыдущая шкала, а близкая к оптимальной, следовательно, построенная шкала также не будет оптимальной;

• 2)    “дефицит” погрешности накапливается с ростом номера шага, то есть в худшем случае СКО построенной шкалы может отличаться от СКО оптимальной шкалы на N А_е .

Отмеченные недостатки алгоритма можно частично компенсировать путем модификации алгоритма. Основная идея модификации состоит в использовании еще одного набора матриц, который также заполняется по ходу алгоритма:

E ⁽ j ) = { E r^Jjk : r е [ L + j , R ], k e [0, K ) } , j e [1, R - L ).

Каждая матрица E ^{( j )} содержит значения погрешностей, которые на самом деле достигаются на соответствующих шкалах. Эти значения могут быть немного меньше, чем требуемые. На каждом шаге предыдущая оптимальная шала выбирается из усло- ( j ) вия того, что ее реальная погрешность E_r ^{( j} _k ⁾ не превышает заданную. Запишем формально такую модификацию алгоритма.

Модификация для шага 1

Кроме матриц значений последней границы B ⁽¹⁾ и значений энтропии H ⁽¹⁾ , заполняется (1)

матрица E ^{( )} реальных погрешностей, которые в действительности достигаются на построенных оптимальных шкалах:

• (1)      (1)       (1)

E r , k = ^£ ( ^r , B r , k ).

Модификация для шага j

Индекс t (4),(5) предыдущей оптимальной шкалы выбирается, исходя из реального значения погрешности:

t = arg max { E j¹ : E^ kk ^-1)<  k A_e-s 2 ( d , r ) }    (8)

Другими словами, раньше при расчете по формуле (4) в качестве оптимальной левой подшкалы выбиралась шкала предыдущего шага, требуемое значение погрешности для которой не превышало заданную погрешность. Реальная погрешность такой шкалы могла быть существенно (на j А_е ) меньше требуемой. Теперь при расчете по формуле (8) в качестве оптимальной левой подшкалы выбирается шкала предыдущего шага, реальная погрешность которой наиболее близка к требуемой и не превышает ее.

Для доступа к реальным погрешностям на следующем шаге строятся матрицы реальных погрешностей E ^{( j )} :

Е ( ^j) - е^{( j-1)}+г2(В(^j ) г)

E r , k = E r , w ^{+e (} B r , k , ^r ) ■

Легко видеть, что при таком способе построения шкал, погрешность на каждом шаге не может отличаться от заданной более, чем на А_е :

(k - 1)Ае < E^ < kАе.

Матрица реальных ошибок используется также на этапе собственно построения шкалы. Модификация здесь заключается в том, что индекс w (6), (7) следующей границы также выбирается исходя из реального значения погрешности:

N - 2

Er-j-1L E(j-1) < ^max - Se(bi,bi+1)- ■ i=j+1

w = arg max' k

Использование матрицы реальных погрешностей приводит к тому, что конечная шкала будет отличаться от оптимальной не более, чем на А_е , а не на N А_е , как раньше.

5.    Вычислительный эксперимент

Для оценки эффективности разработанного алгоритма построения оптимальных шкал был проведен ряд вычислительных экспериментов. В качестве функции распределения вероятностей квантуемой величины рассматривалась биэкспоненциальная функция:

f ( x ) = A exp ( -a| x |) , | x | <  127

где A - нормировочный коэффициент, a - параметр, определяющий дисперсию сигнала. Симметричность этой функции позволяет ограничиться рассмотрением шкал, имеющих представительное значение в начале координат и симметричных отно- сительно него. Согласно [2], такая функция распределения соответствует важному для практики частному случаю, когда роль квантуемой величины играет разностный сигнал, который получается вычитанием предсказанных значений отсчетов исходного сигнала из его истинных значений (в качестве исходных здесь рассматриваются сигналы (изображения) в байтовом формате). Такая ситуация характерна, в частности, для дифференциальных (разностных) методов компрессии изображений, например для ДИКМ [2] и его обобщений, таких как CTPI [5] и MLGI [6, 7].

Для описанного частного случая были построены равномерные шкалы, шкалы Макса и оптимальные шкалы, вычисленные по разработанному алгоритму. Некоторые результаты показаны на рис. 2 в виде графика зависимости энтропии квантованного сигнала от погрешности представления им исходного сигнала. При построении равномерных шкал и шкал Макса варьировалось количество интервалов квантования и в каждом случае вычислялось СКО и энтропия. Для построения квазиопти-мальных шкал при каждом заданном значении СКО применялся разработанный алгоритм, а затем вычислялись получившиеся значения СКО и энтропии.

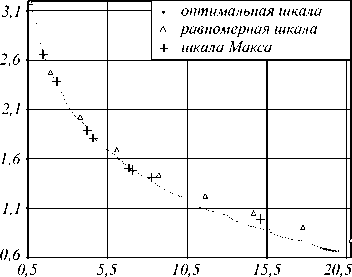
Рис. 2. Зависимость энтропии от погрешности для различных шкал квантования при a = 0,2.

На основании полученных результатов можно сделать следующие выводы.

• 1.    При малых допустимых погрешностях все рассмотренные шкалы близки к оптимальным.

• 2.    Построенные разработанным алгоритмом оптимальные (квазиоптимальные) шкалы по качеству не уступают равномерным шкалам и шкалам Макса, а при больших допустимых погрешностях имеют преимущество, которое увеличивается с ростом допустимой погрешности.

• 3.    Предлагаемые шкалы образуют в координатах “погрешность-энтропия” множество, достаточно плотно заполняющее область рассматриваемых погрешностей, что позволяет построить необходимую оптимальную шкалу при любой заранее заданной допустимой погрешности.

• 4.    Выявленные достоинства разработанных шкал позволяют рекомендовать их применение в задачах компрессии.

Заключение

В работе рассмотрены вопросы построения оптимальных шкал квантования в задаче компрессии цифровых сигналов. Сформулирован критерий оптимальности шкалы квантования с точки зрения эффективности последующего статистического кодирования квантованного сигнала. Разработан алгоритм построения шкал квантования, оптимальных по сформулированному критерию. Проведено исследование разработанного алгоритма и сравнение построенных шкал квантования с наиболее распространенными шкалами. Показано, что построенные шкалы имеют ряд преимуществ, по сравнению с известными.