Оптимальное проектирование цилиндрических оболочек при неравномерном нагружении
Автор: Дедов Николай Иванович, Исуткина Вера Николаевна
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Машиностроение и машиноведение
Статья в выпуске: 4-2 т.18, 2016 года.
Бесплатный доступ
В статье рассматривается алгоритм проектирования цилиндрической оболочки минимального веса при неравномерном нагружении. Задачи оптимизации несомненно представляют особый интерес для конструкций с большим числом геометрических параметров, геометрических и физических ограничений. В данной задаче оптимальный проект отыскивается в классе конструктивно - ортотропных оболочек. Алгоритм многопараметрического оптимального проектирования предусматривает использование эффективного метода декомпозиции, позволяющего свести задачи большой размерности к решению ряда более простых задач. Задача поиска минимального веса цилиндрической оболочки является задачей нелинейного программирования и представляет большой интерес для практических приложений при проектировании тонкостенных оболочечных конструкций.
Алгоритм, оптимальное проектирование, метод декомпозиции, подкрепленная оболочка, целевая функция, напряжение, устойчивость
Короткий адрес: https://sciup.org/148204681
IDR: 148204681 | УДК: 539.3
Текст научной статьи Оптимальное проектирование цилиндрических оболочек при неравномерном нагружении
продольными и кольцевыми ребрами получим в виде [1]
T i ( б , Ф ) = - N 6 - M 6 - £ Q nc e - " • cowcos "6 - 2 n r n r n = 2
to
-^qnse-" sinn^ cos"6, n=2
где 6 =--безразмерная координата в про-r дольном направлении, ф - угловая координата в кольцевом направлении, N(6), M(5)- осевая сила и изгибающий момент, действующие на цилиндрическую подкрепленную оболочку, qnc , qns –коэффициенты разложения осевой нагрузки в ряд Фурье, h, r - толщина и радиус цилиндрической оболочки. Внутреннее усилие Т1 (§ф) изменяется в продольном и поперечном направлениях.
Окружные усилия определяем от действия внутреннего давления, изменяющегося в продольном направлении
T2(6) = P(6)Г ,
где P ( б ) - внутреннее давление.
Оптимизацию веса подкрепленной цилиндрической оболочки осуществляем по параметрам толщины обшивки h , площади продольного набора F 1 , площади поперечного набора F 2 , шагов продольного и поперечного наборов l 1 , l 2 соответственно. При оптимальном проектировании должны учитываться условия прочности, устойчивости и жесткости, а также конструктивные и технологические ограничения.
Целевую функцию веса подкрепленной цилиндрической оболочки выразим через параметры проектирования x 1 , x 2 , x 3 , x 4 , x 5 [2]
G = 2nr 2 Lyw10 — ,
W = x 1
0,01 mx9x, 0,01 m x.x,
+- 124 + 235
2 n L 0
h 102
где x 1 = --параметр толщины обшивки, r
F 104 F 2 104
x2 = 1 , x3 = ---параметры пло- r2 r2
щадей продольного и поперечного наборов, x4 = m1, x5 = m2 - количество продольных и поперечных ребер, L0 =--параметр длины r цилиндрической оболочки, mi — коэффициент наличия подкрепляющего набора, у — удельный вес материала конструкции оболочки.
Целевая функция определяется компонентами вектора геометрических параметров X . Система ограничений, которым должен удовлетворять вектор X , состоит из геометрических ограничений и физических ограничений по требованиям прочности и устойчивости.
Предельные ограничения для геометрических параметров представлены в виде пяти неравенств
/ х min x. , - q, (x)=--------^ i, i = 1,5, xi где min xi — минимально допускаемое значение геометрического параметра из конструктивных и технологических соображений, xi — значения геометрических параметров в процессе оптимизации конструкции подкрепленной цилиндрической оболочки. Дополнительные ограничения накладываются на геометрические размеры продольных и поперечных ребер в зависимости от формы их сечений.
На рис. 1 показан элемент конструкции цилиндрической подкрепленной оболочки с геометрическими размерами подкрепляющих ребер, шаг продольных и кольцевых ребер и толщина цилиндрической оболочки. Подкрепляющие ребра имеют сечение в виде прямоугольника.
Физические ограничения по прочности обшивки и подкрепляющего набора в продольном и поперечном направлениях запишем в виде q,= ^ ^ 1, [f ]
i = 1,2,
где f i - меридианальные или окружные напряжения, действующие в элементах конструкции оболочки, [ f ] — допускаемое напряжение по прочности материала конструкции оболочки.
Ограничения по устойчивости учитывают местную и общую потерю устойчивости подкрепленной цилиндрической оболочки. Местная потеря устойчивости обшивки между ребрами рассматривается как устойчивость пластины с шарнирно опертыми краями, а ребра как устойчивость пластины с тремя шарнирно опертыми краями и с четвертым свободным краем [3]
2 h 2
° кр» = k 1 Eh- , f„ = k 2 E f ,
V l1 7 V b 7
где k 1 = 3,6 — коэффициент для определения критического напряжения пластины, k 2 = 0,42 — коэффициент для определения критического напряжения для ребра.
Критическая сила общей потери устойчивости подкрепленной цилиндрической оболочки [4]
Nкр = min { [m'^2D1 / L0 ]^m (в)} , в = nL^ , 1 m, n mn где m, n — количество полуволн в продольном и поперечном направлениях.
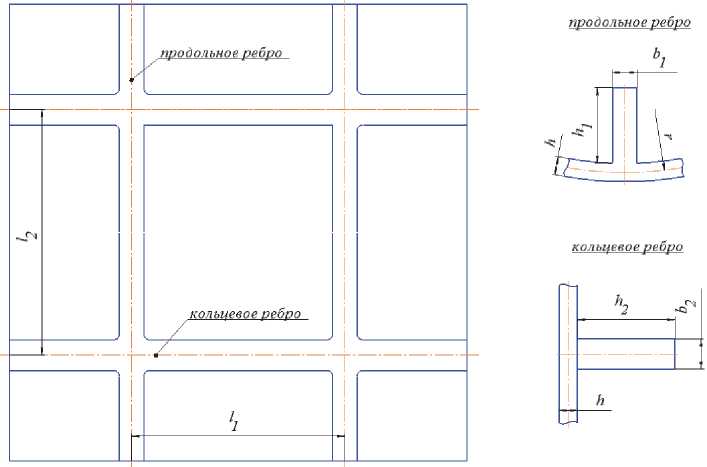
Рис. 1. Элемент конструкции цилиндрической подкрепленной оболочки
В ограничениях по устойчивости введены параметры
N = N^ kp 2nr 2 E
_ ст -104 ст =
E
Ограничения по местной устойчивости q, (x ) = CT ^ 1, i = 1,2, сткр, i где ст - — критические напряжения обшивки и кр.i ребер.
Ограничения по общей устойчивости подкрепленной цилиндри ч еской оболочки
4i(x ) = TN" i = 1,2, кр.i где Nкр i — критическая нагрузка общей потери устойчивости по несимметричной и симметричной формам.
При решении задач оптимизации большой размерности используется метод декомпозиции [5]. Декомпозиция задачи оптимального проектирования проведена не только на уровне исходной постановки задачи, но и на каждом шаге вычисления алгоритма, основанного на замене исходной задачи последовательностью упрощенных подзадач. Характерной причиной всех методов декомпозиции является снижение требований к мощности ЭВМ, удобству использования ограничений, связанных только с решаемой простейшей подзадачей.
В данном случае задача многопараметрического оптимального проектирования разбивается на три подзадачи меньшей размерности. Для решения первой подзадачи используется метод деформированного треугольника (рис. 2).
В результате решения первой подзадачи методом деформированного треугольника определяется оптимальное количество продольного и поперечного набора оболочки.
На геометрические параметры подкрепленной оболочки накладываются конструктивные ограничения m1min L 2пг m7 = —, m2 =----. l1 l2 В координатах x4, x5 выбираются три точки, не лежащие на одной прямой, для которых вычисляются значения целевой функции веса W. Метод деформированного треугольника заключается в замене исходного треугольника на новый, при этом «худшая» вершина треугольника отбрасывается и заменяется более подходящей точкой со значением целевой функции веса Wp на каждой итерации. Рис. 2. Метод деформируемого треугольника «Худшая» вершина деформируемого треугольника определяется из сравнения значений целевых функций веса в трех вершинах треугольника W3>W2>W1. Вершина треугольника с наибольшим значением целевой функции веса W3 считается «худшей». Определим центр тяжести двух вершин W1 , W2 12 12 _ x 4 + x 4 _ x 5 + x 5 X4c 2 , x 5 c 2 , построим координаты пробной точки xn = xc + a( xc— x з), где a>0 и вычислим значение целевой функции Wn. Точка xn получается отражением точки x3, а коэффициент а называется коэффициентом от- ражения. Проводится анализ значений целевой функ- ции веса в вершинах полученного треугольника W1, W2, Wn. В зависимости от значения величины Wp возможны следующие случаи. 1. Если значения W2>Wn>W1, то точка x3 заменяется на точку xn и итерации продолжаются. 2. Если значение Wn 3. Если значение Wn>W2, то треугольник необходимо сжимать и точка xp перемещается в направлении точки x3. Координаты этой точки определяют по формулам определением координаты точки в этом направ- лении по формуле xp = xc + в(xn—xc ), где P>1 - коэффициент растяжения. Если Wp xo = xc + X(x3—xc ), если Wn^ W3, Xo = Xc + Y(Xn—Xc), если Wn< W3, где 0<y<1 - коэффициент сжатия. Если значение W0<min(Wn , W3 ), то точка x3 заменяется на точку xo. В случае невыполнения условия процесс итераций продолжается. Точка xp получается отражением точки x3, а коэффициент a называется коэффициентом отражения. В процессе итераций при деформировании треугольника помимо отражения используется процедуры растяжения и сжатия вершин треугольника, а также периодически проводится замена текущего треугольника на правильный. При этом используются две «лучшие» вершины текущего треугольника. Для решения второй подзадачи, определения оптимальных значений толщины обшивки и площадей поперечного набора, предлагается алгоритм, основанный на применении метода спуска по градиенту. Вначале осуществляется спуск на границу допустимой области из точки «s», находящейся на плоскости равного уровня целевой функции, на которой W = W0 W dw х. = х. — et °-^--- "k ‘'5 Р ]VW|\2 dXi’ где xis — координата точки s, в — коэффициент, определяющий величину шага по градиенту, IIVW — модуль градиента целевой функции, d W „ , – проекция градиента целевой функции d Xi веса, t — число шагов до активного ограничения. Далее вычисляются координаты точки «О», удаленной от активных ограничений на расстояние, равное среднеарифметическому расстоянию до активных ограничений по различным направлениям Xi о = Xis + R 0, ,o ,s ,o 1 M _ где Ri,o = M " 2^ Rik " ni,k ^^^^^^^^ координата вектора, ni k — проекция единичного вектора выбранного направления на плоскость равного уровня. В результате решения третьей подзадачи определяются геометрические размеры сечений подкрепляющих продольных и кольцевых ребер по заданным площадям. В качестве примера исследуем определение оптимальных геометрических характеристик цилиндрической оболочки подкрепленной внутренними продольными и кольцевыми ребрами прямоугольного сечения. Геометрические характеристики: радиус цилиндрической оболочки 3,85 м, длина 11 м. Подкрепленная цилиндрическая оболочка нагружена осевой сжимающей силой, которая изменяется вдоль образующей. Интенсивность несимметричной распределенной по торцу оболочки нагрузки меняется от – 1650 кН/м до 1100 кН/м. Переменное по длине оболочки давление на внутренней ее поверхности меняется по линейному закону в сечениях в пределах от 0,322 МПа на нижнем торце оболочки до 0,121 МПа на верхнем торце. Алгоритм оптимизации подкрепленной цилиндрической оболочки позволяет определять оптимальные значения толщин обшивки в сечениях оболочки, площадей ребер продольного и кольцевого наборов, количество продольных и кольцевых ребер. При наличии нескольких значений давления в сечении оболочки расчет оптимальных параметров проводится для давления, соответствующего большему нагружению конструкции. Результаты расчетов оптимальных геометрических параметров подкрепленной цилиндрической оболочки приведены в таблице. Расчеты проведены для 12 сечений, начиная с нижнего торца оболочки. В результате расчета оптимальный шаг продольных ребер получается переменным вдоль образующей оболочки, что недопустимо с точки зрения рациональной работы конструкции на осевые нагрузки, так как передача усилий ребрами со смещенными осями потребует увеличение веса конструкции. Поэтому, оптимальный шаг продольных ребер должен быть постоянным для всей оболочки. Необходимо провести решение очередной подзада- Таблица. Результаты расчетов оптимальных геометрических параметров подкрепленной цилиндрической оболочки № сечения 1 2 3 4 5 6 7 8 9 10 11 12 Тi 10-2, кН 325 260 211 159 182 238 174 144 236 304 287 222 11 102, м 18,7 16,4 14,4 12,0 13,5 16,6 14,6 15,1 15,9 17,4 16,3 14,4 12102, м 19,9 22,1 17,1 15,8 15,7 14,6 16,8 183 16,1 20,3 14,0 14,1 F1 104, мм2 1,87 1,76 1,53 1,37 1,42 1,29 1,18 1,39 1,36 1,32 1,23 0, 98 F2 104, мм2 2,26 2,3 2,11 1,98 1,83 1,80 1,76 1,67 1,61 1,56 1,29 1,16 h 103, м 3,6 3,4 3,3 3,2 3,2 3,1 3.0 2,9 2,8 2,7 2,6 2,6 h 1 103, м 45 44 38 34 36 32 30 34 34 33 31 25 h2103, м 56 57 53 50 46 45 44 42 40 39 32 29 чи оптимизации геометрических характеристик подкрепленной оболочки, которая заключается в выборе одного шага из 12, который и будет оптимальным для всей конструкции. Указанная подзадача может быть решена также для определения постоянного шага кольцевых ребер. Конкретное решение о выборе шага продольных и кольцевых ребер принимается с учетом технологических и экономических требований к проектируемой конструкции. Разработанный алгоритм оптимального проектирования несимметрично нагруженных цилиндрических подкрепленных оболочек позволяет проектировать реальные оболочечные конструкции переменного сечения.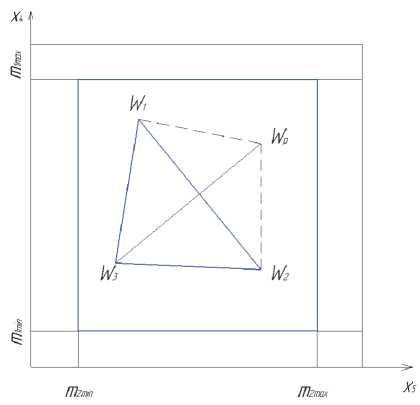
Список литературы Оптимальное проектирование цилиндрических оболочек при неравномерном нагружении
- Моссаковский В.И., Гудрамович В.С., Макеев Б.М. Контактные задачи теории оболочек и стержней. М.: Машиностроение, 1978. 248 с.
- Рябов А.А., Столяров Н.Н. Весовая оптимизация продольно сжатых подкрепленных цилиндрических оболочек//Тр. семинара. Вып. ХII. Казань: 1979. С.161-171.
- Вольмир А.С. Устойчивость упругих систем. М.: Наука, 1967. 984 с.
- Маневич А.И. Об устойчивости эксцентрично подкрепленной цилиндрической оболочки//Тр. Всесоюзной конференции по теории оболочек и пластин. Днепропетровск, 1969. М.: Наука, 1970. С.403-407.
- Цурков В.И. Декомпозиция в задачах большой размерности. М.: Наука. 1981, 362 с.


