Оптимальное проектирование трехслойной балки при заданных частотах поперечных колебаний

Трехслойные конструкции, состоящие из тонких несущих слоев и заполнителя, широко используются в авиации, космической технике, судостроении и строительстве. Это обусловлено высокой степенью весового совершенства трехслойных балок, пластин и оболочек. К настоящему времени существует несколько сложившихся и широко используемых в расчетной практике моделей трехслойных конструкций [1-10]. Тем не менее, несмотря на выполненные исследования, интерес к моделированию трехслойных конструкций не ослабевает. Особенно это относится к задачам оптимального проектирования трехслойных конструкций, используемых в современной технике.

Рассмотрим задачу выбора оптимальных параметров трехслойной балки при наличии ограничений, накладываемых на собственные частоты поперечных колебаний. Отметим также, что одномерную модель балки из-за ее относительной простоты часто используют для предварительного анализа более сложных моделей трехслойных пластин и оболочек.

Рассмотрим трехслойную балку с прямоугольным поперечным сечением и свяжем ее с системой координатА, У, Z (рис. 1). Пусть продольная ось А' проходит через центры поперечных сечений балки. Оси У и Z расположим перпендикулярно осиА. Длину балки обозначим /, ширину поперечного сечения - Ь, толщину заполнителя У. а толщину одинаковых несущих слоев - 7 В дальнейшем будет рассматривать движение балки только в i плоскости АУ

Рис. 1. Трехслойная балка с прямоугольным поперечным сечением

В уравнениях (1).. .(3) t - время, Q - перерезывающая сила, М- изгибающий момент, w - прогиб балки, 0 - угол поворота поперечного сечения, X - кривизна балки, V - сдвиговая деформация, D, К- изгибная и сдвиговая жесткости балки, В _р - инерционный параметр балки, D _p - инерционный параметр, связанный с поворотом поперечного сечения балки.

Определим жесткостныеD, Ки инерциальные В _р , D _p параметры балки, используя подход, получивший наибольшее распространение при расчете трехслойных конструкций [10]. В соответствии с этим подходом несущие слои будем считать настолько тонкими, что их изгибная жесткость может быть принята равной нулю. Возникающие в несущих слоях мембранные усилия обеспечивают восприятие изгибающего момента, а заполнитель обеспечивает совместную работу несущих слоев и восприятие перерезывающей силы. Для такой модели трехслойной балки жесткостные и инерционные параметры могут быть записаны в следующем виде:

D = E t — b K = G 8 b, 2 ’                 ’

δ ² δ ³

b p = ⁽² P t t ⁺ P _S ^{8 )} b , D p = ⁽ P tt — ⁺ P ₅ —) ^b ,     (4)

где E - модуль упругости материала несущих слоев; G - модуль сдвига заполнителя; Pt - плотность материала несущих слоев; P8-плотность заполнителя.

Получим уравнения движения балки, содержащие в качестве неизвестных прогиб w и угол поворота 6 . Подставляя (2) и (3) в (1), будем иметь

-

∂2w    ∂θ∂

K dx2 K дx BP д t2’

∂w    ∂2θ∂

_ + D -у ^- K ^6- D P -2 = ⁰ .

∂x∂

Следуя методу разделения переменных, представим решение уравнений (5) в виде

w ( x, t ) = w ( x ) sin to t , 6 ( x, t ) = 6 ( x ) sin to t ,      (6)

Система уравнений, описывающая поперечные колебания трехслойной балки в рамках сдвиговой модели [11], включает уравнения движения

∂ Q    ∂ ² w    ∂ M

—- B. Т = о , —

∂x    ρ∂t       ∂x физические соотношения

-

Q -Ч^т = о; (1)

M = D x , q = к V ;            (2)

геометрические соотношения ∂θ ∂ w

X = —, ш = 6 +— д х ’ ^Ж дx

.

где to - круговая частота колебаний. Подставляя (6) в (5), получим следующую систему однородных обыкновенных дифференциальных уравнений:

-K ∂2w2 -K∂θ-Bρω2w=0, dx      дx                           (7)

K ^∂ w - D ^∂θ ₂ + K θ- D _ρ ω ² θ= 0. ∂ x     ∂ x          ^ρ

Для удобства анализа преобразуем уравнения (7) к безразмерному виду. Введем новую продольную коор

динату а , связанную сх равенством

x

а = -.

l

Переменная а изменяется в пределах от 0 до 1. Подставляя (8) в (7), после некоторых преобразований получим следующие уравнения:

d ² w   du

-%—у-%--n w = 0,

d a   d а dw d2u

%---7 + %u -Пф u = 0,

d а d а

где и = 6 /;

u = -о A₁ e ^а + о A 2 e ^{- r а} - i т A₃ e^{p а} + i т A₄e ^{- ip а} .    (22)

Используя формулу Эйлера e ±ip а = cos p а ± i sin p а, преобразуем выражения (18) и (22) к следующему виду: w = C1chr а + C2shr а + C3 cos pа + C4 sin pа, u = -C1оshr а - C2оchr а + C3 cos pа - C4т cos pа.(23)

Здесь Сп (п = 1, ...,4) новые постоянные интегрирования, связанные с величинами^ (п = 1,..., 4) формулами

C C C - C.

Л K ,2.       ^D р

% = —l ; ф = ^ГЕ~

D       l ² В р

A = 1 ' ^²

¹           2 ^,

2 ^,

(Ю)

B _P ®² 1 ⁴

n = —

D

.

Исходя из уравнений (9), задача расчета частоты колебаний сводится к определению частотного параметра 9 , величина которого в свою очередь зависит от параметров % и ф , содержащих всю информацию о размерах, упругих и инерционных свойствах трехслойной балки.

Представим решение уравнений (9) в следующем виде

C 3 = A 3 + A 4 , C 4 = i ( A ₃ - A 4 ) •

Выражения (23) представляют собой общее решение однородной системы дифференциальных уравнений (9).

Для определения постоянных интегрирования С (п = 1,..., 4) необходимо воспользоваться граничными условиями. Рассмотрим балку, жестко закрепленную на краях. Граничные условия с учетом равенства (8) примут вид

а = 0, w = 0, и = 0,

w = Ae ^а , u = Be ^а ,

гдеА, В и s - неизвестные числа.

Подставляя (12) в (9), получим однородную систему линейных алгебраических уравнений

-(%s2 + n) A - % sB = 0, % sA-(s2 -% + Пф)В = 0.

Уравнения (13) совместны относительной и В, если определитель системы равен нулю:

а = 1, w = 0, и = 0.

Подставляя (23) в (24), будем иметь С ₁ + С ₃ = 0 , С ₂ о + С ₄ т = 0 ,

C ₁chr + C ₂shr + С ₃ cos р + С ₄ sin р = 0 , - C ₁ о shr - C ₂ о chr + C ₃ т sin p - C ₄ т cos p = 0 . Исключая из (25) постоянные С₃ и С₄, получим C ₁ т (chr - cos p ) + C ₂( т shr -о sin p ) = 0, - ^( о shr + т sin p ) + C ₂ о ( - chr + cos p ) = 0.

det -

- ( % s ² + n )       -% s

%s     —(s —% + Пф)

= 0.       (14)

Раскрывая определитель, получим следующее характеристическое уравнение:

% s ⁴ +п (1 + %ф ) s ² -п ( %-Пф ) = 0 •

Однородные уравнения будут иметь нетривиальное решение, если определитель системы будет равен нулю: т(chr - cos p)    т shr -о sin p det - (         F)                 F ^ = 0. (27)

[- ( о shr + т sin p ) о ( - chr + cos p )

Раскрывая определитель (27), получим

Четыре корня этого уравнения представим в виде

22 ^{о -т}

1 - chr cos p +-- shr sin p = 0.

2от

s ₁ = r , s ₂ = - r , s ₃ = ip , s ₄ = - ip , где i - мнимая единица;

r =

-n (i + %ф ) + ТПо+Тф^+^хПл-чф )

2%

;

Р =

П(1 + %ф) + 7 П2 (1 + %ф)2 + 4%n(% — ПФ)

2%

.

Таким образом, решение уравнений (9) имеет вид

w = A ₁ e r ^а u = В₁ e ^а ■

+ A 2 e ^{- r а} + A 3 e i ^а + A ₄ e ^{- ip а} ,

+ В 2 e

.-I

^{r а} + В ₃ б^{р а} + В ₄ e ^- ip ^а .

Установим взаимосвязь между постоянными В

( иА п п

Неизвестным в этом трансцендентном уравнении является частотный параметр 9 . Уравнение (28) имеет бесчисленное множество корней 9 _к (к = 1,2, _, ^ ). Каждому корню 9_к соответствует, согласно формуле (11), своя частота колебаний щ , .

Таким образом, задача определения частоты колебаний трехслойной балки для рассматриваемых граничных условий сводится к решению уравнения (28).

Выполним далее анализ влияния параметров % и ф на частотный параметр 9 . Используя равенства (4), преобразуем выражение (10) к виду

(п =1,..., 4). По первому уравнению системы (13) для каждого sn (п = 1,..., 4) будем иметь

В₁ = -о A , В ₂ = о A 2 , В ₃ = i ^{- 1} т A 3 , В ₄ = - i ^{- 1} т A₄ , (20)

где

1 + 1 Р 8 ⁸

% = 2      ⁸ , ф= 1 2 ^{6 р} *\ .

E ⁸ t 4 L (1 + 1 P l ⁸ ) ^{8       2} P t t

% r ² +n ^о =—;

% r

% ² p ² т =——

-

% p

.

Подставляя (20) в (19) и учитывая равенство i ¹ =-i, получим

По формулам (29) следует, что параметры % и ф зависят от нескольких соотношений G / Е, / / 8 , 8 / t и р ₈ / р ₍. Для реальных трехслойных конструкций с тонкими несущими слоями диапазон изменения этих соотношений вполне определен [1; 4]. Это позволяет задать диапазон изменения параметра % от 50 до 1 ООО, а диапазон изменения параметра ф - от 0,000 1 до 0,001.

Задаваясь различными сочетаниями параметров % и ф и решая уравнение (28), определим зависимость д _к( % , ф ). Значения в k = 4/пГ (к = 1,3,5) представлены в табл. 1^3, а зависимости Р _к (к = 1, 3,5) для рассматриваемых диапазонов изменения параметров % и ф приведены на рис. 2.. .4. Верхний график на рисунках соответствует ф = 0,000 1, а нижний - ф = 0,001.

Таблица 1

Значение параметра P _t

%	ф
	0,0001	0,000 25	0,000 5	0,000 75	0,001
50	4,463	4,462	4,461	4,460	4,459
100	4,590	4,589	4,587	4,585	4,583
200	4,658	4,656	4,653	4,651	4,648
300	4,681	4,679	4,676	4,673	4,670
400	4,693	4,691	4,688	4,685	4,681
500	4,700	4,698	4,695	4,691	4,688
600	4,705	4,703	4,699	4,696	4,693
700	4,708	4,706	4,703	4,699	4,696
800	4,711	4,709	4,705	4,702	4,698
900	4,713	4,711	4,707	4,704	4,700
1000	4,714	4,712	4,709	4,705	4,702

Таблица 2

Значение параметра Р ₃

%	ф
	0,0001	0,000 25	0,000 5	0,000 75	0,001
50	8,347	8,347	8,347	8,347	8,347
100	9,245	9,240	9,233	9,225	9,218
200	9,932	9,919	9,898	9,877	9,856
300	10,225	10,207	10,177	10,147	10,117
400	10,389	10,367	10,331	10,295	10,259
500	10,493	10,469	10,428	10,388	10,349
600	10,566	10,539	10,496	10,453	10,410
700	10,619	10,591	10,545	10,500	10,455
800	10,660	10,631	10,583	10,535	10,489
900	10,692	10,662	10,612	10,563	10,516
1000	10,718	10,687	10,636	10,586	10,537

Таблица 3

Значение параметра Р ₅

%	ф
	0,0001	0,000 25	0,000 5	0,000 75	0,001
50	10,905	10,907	10,911	10,914	10,918
100	12,504	12,503	12,500	12,497	12,494
200	13,987	13,971	13,943	13,915	13,886
300	14,733	14,702	14,648	14,594	14,539
400	15,191	15,146	15,070	14,994	14,917
500	15,502	15,446	15,351	15,257	15,162
600	15,728	15,662	15,552	15,443	15,335
700	15,900	15,825	15,703	15,581	15,462
800	16,035	15,953	15,820	15,688	15,559
900	16,143	16,056	15,913	15,773	15,636
1000	16,233	16,141	15,990	15,843	15,699

Отметим, что использование в численных примерах частотного параметра Рк вместо параметра ек обуслов лено тем, что первый из них традиционно применяется в моделях, не учитывающих деформацию поперечного сдвига и инерцию поворота поперечного сечения. Поэтому параметр Рк удобен при сравнении результатов, полученных по различным моделям. Для классической теории балок, в которой ^ ^ ^ и Dp = 0, параметр Рк имеет следующие значения [12]:

Р , =4,730; Р ₂= 7,853, Р ₃= 10,996, Р ₄= 14,137, Р ₅= 17,279. (30)

Рис. 2. Изменение параметра Р ₁

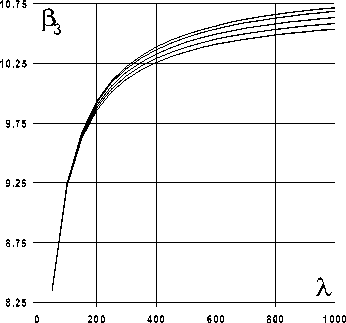
Рис. 3. Изменение параметра Р ₃

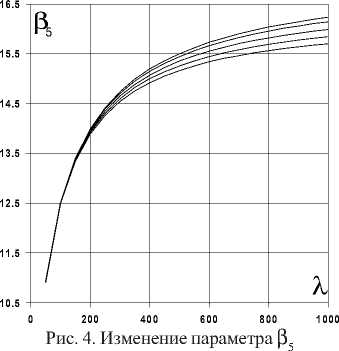
Перейдем к анализу результатов, приведенных в табл. 1.. .3 и на рис. 2... 4. Влияние параметра %, а значит, и деформации поперечного сдвига на частотный параметр особенно заметно в диапазоне от 50 до 400 и увеличивается от Р1 к Р5. Параметр ф, характеризующий инерцию поворота поперечного сечения, оказывает незначи- тельное влияние на первый частотный параметр (см. рис. 2). Инерция поворота влияет на динамическое поведение балок тем больше, чем выше тон колебаний, определяемый числом к (см. рис. 3, 4).

О необходимости учета влияния деформации сдвига и инерции поворота на частотные параметры можно судить, сравнивая значения (30) с данными этой статьи. Величины отклонений найденных частотных параметров от классических результатов (30) для % = 50, 1 000 и ф = 0,000 1,0,001 приведены в табл. 4.

m = lb (2 р t t + р ₈ 8 ) .                (33)

Длина / и ширина Ъ, как правило, известны. Поэтому необходимо отыскать такие проектные параметры Е, G, 8 , t, 6 _g и 6 ₍, при которых масса балки (33) имеет минимальное значение. Пространство проектирования удобнее всего задать в виде следующих неравенств:

min

min

¹ max ^,     min

? ,8 <8<8 , max, min          max,

„   „           „ „     (34)

„ , Ps„ <р8<р8„ , р,„ <р <р,„ .

max ^,    8 min 8      8 max ^, t min t t max

Задача минимизации массы решается в общем слу-

Таблица 4

Величины отклонений частотных параметров, %

X	9	к = 1	к = 2	к = 3
50	0,000 1	5,99	31,74	58,45
	0,001	0,06	31,73	58,25
1000	0,0001	0,34	2,59	6,44
	0,001	0,60	4,35	10,06

Результаты вычисления частотных параметров вк (к = 1,..., 5) могут быть представлены в виде аналитических зависимостей. Используя метод наименьших квадратов, получим в k = £ Ajk 'b-j (k-1,...,5),          (31)

j = 1

где

A jk = R jk + T jk Ф .                 (32)

Значения коэффициентов R_jk и T_jk приведены в табл. 5 и 6.

Рассмотрим далее задачу оптимального проектирования трехслойной балки при наличии ограничений, накладываемых на частоты колебаний. Традиционной постановкой задачи оптимизации является отыскание экстремума некоторой целевой функции в заданном пространстве проектирования, при наложенных ограничениях. Наиболее часто в качестве целевой функции выбирается масса конструкции, а в качестве критерия оптимальности - ее минимум.

Масса трехслойной балки

чае методами математического программирования с использованием итерационной процедуры последовательного улучшения конструкции. Отметим, что при реальном проектировании эта задача часто сводится к определению толщин 8 и t, обеспечивающих минимум массы для выбранных модулей упругости и плотностей. В процессе оптимизации для вычисления параметра П = в 4 можно использовать формулы (31) или данные из табл. 1...3, определяя, если надо, промежуточные значения с помощью интерполяции.

Рассмотрим в первую очередь постановку задачи проектирования с единственным ограничением - заданной частотой колебаний to _k . По формулам (11) и (4) будем иметь

1 ω _k = 2

δ η k l 2

E ρ (1 + 1 ^{ρ δ δ} ). ^t 2 ρ _t t

Тогда ограничение можно записать в виде равенства

1 ω _k - 2

η k

^E = 0. ρ t (1 + 1 ^{ρ δ ρ} )

2 ρ _t t

Равенство (36) выполняется при определенных значениях толщин 8 и t. Оптимальными будут те из них, при

которых масса балки (33) достигает минимума.

Рассмотрим постановку задачи о выборе проектных параметров трехслойной балки для случая, когда ограничения накладываются на несколько частот колебаний to _k

Таблица 5

Значения коэффициентов R._k

j
к	1	2	3	4	5
1	4,730 ■ 10 0	-1,455 ■ 101	6,497 ■ 10 1	-3,074 ■ 102	4,179 ■ 10 3
2	7,853 ■ 10 0	-9,.008 ■ 101	2,303 ■ 103	-5,736 ■ 104	7,999 ■ 105
3	1,099 ■ 101	-2,657 ■ 102	1,364 ■ 104	-5,496 ■ 105	1,008 ■ 107
4	1,411 ■ 101	-5,649 ■ 102	4,239 ■ 10 4	-2,133 ■ 106	4,389 ■ 107
5	1,718 ■ 101	-9,834 ■ 10 2	9,262 ■ 10 4	5,253 ■ 106	1,148 ■ 108

Таблица 6

Значения коэффициентов Т._к

к	j
	1	2	3	4	5
1	-1,443 ■ 101	7,850 ■ 102	-1,770 ■ 104	3,581 ■ 105	-6,318 ■ 106
2	-8,763 ■ 101	1,132 ■ 104	-7,632 ■ 105	3,083 ■ 107	-5,446 ■ 108
3	-2,519 ■ 102	5,675 ■ 104	-6,180 ■ 106	3,457 ■ 108	-7,355 ■ 109
4	-5,209 ■ 102	1,645 ■ 105	-2,282 ■ 107	1,.473 ■ 109	-3,386 ■ 1010
5	-8,805 ■ 102	3,442 ■ 105	-5,470 ■ 107	3,812 ■ 109	-9,127 ■ 1010

(k = 1, 2, ..., г). Целевой функцией здесь по-прежнему является масса балки, а критерием оптимальности - ее минимум. В этой задаче ограничение можно представить в следующем виде:

ω-ω

<8 к (к =1,2,..., г),           (37)

ωk где 8к - некоторые числа меньше единицы. Чем меньше величина 8к, тем больший вес имеет к-я частота. Числа 8к должны удовлетворять условию

r

X (1 -8 к ) = 1 .                 (38)

к = 1

Пространство проектирования задается неравенствами (34).

Кроме критерия оптимальности в виде минимума массы, в этой задаче можно использовать критерий оптимальности, предполагающий минимум суммы квадратов отклонений заданных частот щ _к (к = 1, 2,..., г) от вычисляемых ® _к (к = 1,2, ^, г):

r minX[Yк(щк щк)]2,              (39)

к = 1

где£ к (к = 1,2, .„, г)-весовые множители, которые подчиняются условию

r

X Y к = 1 .                   (40)

к = 1

Область изменения проектных параметров, как и прежде, определяется неравенством (34).

В качестве примера определим толщины 8 и t для трехслойной балки с 1= 1 м, В = 0,1 м, Е = 70 ГПа, G = 300 МПа, pt = 2 750 кг / м3, pg= 50 кг / м3 и заданной частотой колебаний ц = 1 800 с-1. Пространство проектирования задано следующими неравенствами:

0,02 м <8< 0,1м,

0,0001 м <  t <  0,001м. δ

δ

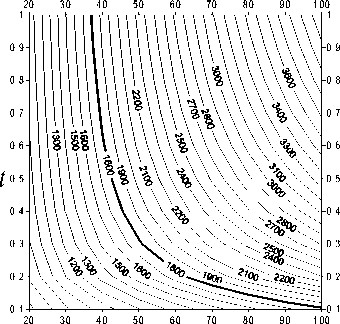
Рис. 5. График изолиний поверхности w.( 8 . t )

Изолинии поверхности щ ₁( 8 , t) (рис. 5), определяемой равенством (35), показывают, что заданная частота колебаний щ = 1800 с^-1 реализуется при определенных соотношениях толщин 8 и t. Подстановка этих значений 8 и t в формулу (33) дает 8 _opt = 0,056 м, t_opt = 0,000 25 м и т_а^ = 0,42 кг

Таким образом, авторами поставлена и решена задача оптимального проектирования трехслойной балки при наличии ограничений, накладываемых на частоты поперечных колебаний. Выполнен анализ влияния деформации поперечного сдвига в заполнителе и инерции поворота поперечного сечения на частотный параметр. Результаты расчетов представлены в виде таблиц и аналитических формул, удобных для использования в проектировании. Определены целевая функция и функциональные ограничения для различных способов задания частот колебаний. Приведен пример выбора оптимальных параметров трехслойной балки.