Оптимальное распределение исполнителей по рабочим местам

Качество решений, связанных с управлением человеческими ресурсами, может быть существенно повышено путем применения оптимизационных методов.

Математические методы, которые в настоящие время имеются в распоряжении исследователя, можно разделить на две основных группы: аналитические и численные.

К аналитическим относятся методы нахождения безусловного экстремума, метод множителей Лагранжа и ряд других. Они позволяют за один просчет получить точное решение задачи. Однако применение аналитических методов возможно лишь при выполнении ряда жестких условий. Так, целевая функция и ограничения задачи должны быть по крайней мере дважды дифференцируемыми функциями, а ограничения, кроме того, иметь вид строгих равенств. Во многих практических задачах эти условия не выполняются, поэтому аналитические методы находят лишь ограниченное применение.

Гораздо чаще для решения управленческих задач применяют численные методы, к которым относятся методы линейного, нелинейного, дискретного, динамического программирования и некоторые другие. Численные методы представляют собой итеративные процедуры, позволяющие получить окончательное решение путем многоэтапных расчетов по определенному алгоритму. Как правило, они предусматривают формирование на первом этапе некоторого первоначального решения и последовательное, шаг за шагом, его улучшение.

В качестве примера приведем ситуацию распределения исполнителей по рабочим местам. Её можно сформулировать следующим образом.

Имеется n исполнителей и n видов работ, которые нужно выполнить. Задана матрица оценок Cij, характеризующих эффективность выполнения i-м исполнителем и j-й работы. Требуется распределить исполнителей по работам так, чтобы можно было выполнить всю совокупность работ наиболее эффективно. При этом для выполнения каждой работы должен быть назначен только один исполнитель, и каждый исполнитель должен быть задействован только на одной из работ.

В специальной литературе подобные задачи называют задачами о назначениях.

Отметим, что для каждой из n работ можно подобрать исполнителя только в том случае, когда любые k исполнителей (1≤k≤n) могут выполнить в совокупности не менее k разных работ. В этом заключается условие разрешимости задачи о назначениях.

В данной задаче искомыми являются переменные xij, i=1…,n, j=1,…,n. Если i-й исполнитель назначен на выполнение j-й работы, то xij=1. В противном случае, xij=0.

С математической точки зрения эта задача относится к задачам линейного программирования. Соответственно, она может быть решена с помощью универсального метода решения задач линейного программирования – симплексного метода. Однако удобнее использовать для этой цели гораздо менее трудоёмкий алгоритм Флада.

В некоторых случаях перед применением алгоритма Флада нужно выполнить определенные предварительные действия.

Если число исполнителей не равно числу работ, то в рассмотрение вводят фиктивных исполнителей или фиктивные работы так, чтобы матрица оценок стала квадратной. Оценки Сij для фиктивных исполнителей (или фиктивных работ) принимают равными нулю.

Если задача решается на максимум целевой функции, то от исходной матрицы оценок Сij нужно перейти к матрице преобразованных оценок С’ij с помощью формулы

С’ij=maxСij - Сij ,                           (1)

где maxСij – наибольший элемент исходной матрицы оценок.

Если задача решается на минимум целевой функции, то исходную матрицу оценок оставляют без изменений.

После этого применяют алгоритм Флада, который предусматривает выполнение следующих действий.

• 1.    В каждой строке матрицы оценок | Сij | находят минимальный элемент и вычитают его из всех элементов данной строки.

• 2.    В полученной матрице в каждом столбце находят минимальный элемент и вычитают его из всех элементов данного столбца.

• 3.    Минимальным числом прямых вертикальных и/или горизонтальных линий вычёркивают все имеющиеся в матрице нули. Если число прямых равно n, то получено оптимальное решение.

• 4.    Если число прямых меньше n, то оптимальное решение не получено. В этом случае среди незачеркнутых элементов матрицы оценок выбирают минимальный элемент, вычитают его из всех незачеркнутых элементов и прибавляют ко всем элементам, зачеркнутым двумя линиями. Остальные элементы матрицы оставляют без изменения. После этого возвращаются к пункту 3 алгоритма.

Целью первых двух этапов является получение, по крайней мере, одного нуля в каждой строке и каждом столбце матрицы оценок.

Оптимальное решение получают в матрице оценок | Сij |. От неё нужно перейти к матрице искомых переменных | xij |, которая имеет такую же размерность (nxn). Элементами матрицы | xij | являются нули и единицы. Приравниваться единице могут те элементы матрицы | xij |, которым соответствуют нули в матрице | Сij |. При этом в каждой строке и каждом столбце сформированной матрицы | xij | должна быть только одна единица.

В первую очередь единицы следует записывать в те строки (столбцы) матрицы | xij | , которые соответствуют строкам (столбцам) матрицы | Сij |, содержащим только один ноль.

Оптимальному решению в матрице |Сij | могут соответствовать несколько матриц | xij |, которые отличаются расположением единиц, но дают одинаковое значение целевой функции. В этом случае имеются несколько разных, но равноценных вариантов распределения исполнителей по работам.

Рассмотрим пример.

Имеется четыре рабочих места и пять кандидатов на эти места, каждый из которых может работать на любом месте. Известна производительность i-го кандидата на j-м рабочем месте Cij. Нужно распределить кандидатов по рабочим местам так, чтобы добиться максимальной суммарной производительности.

Матрица значений Cij приведена ниже. Строки матрицы соответствуют отдельным исполнителям (кандидатам на места), её столбцы – видам работ (рабочим местам в данном случае).

| Cij |= ⁶

10  3

Поскольку число исполнителей превышает число рабочих мест, сначала необходимо сбалансировать матрицу. Для этого добавляем 5-й столбец из нулей, который будет символизировать пятое фиктивное рабочее место.

5  7  10  3  0

Так как данная задача о назначениях решается на максимум целевой функции, то от исходной матрицы оценок Сij нужно перейти к матрице преобразованных оценок С’ij. В нашем случае такой переход осуществляется по формуле С’ij=10 - Сij:

5  3  0  710

2  1  6  210

6  7  4  510

5  3  2  610

4  1  3  110

После этого для нахождения оптимального решения может быть применён алгоритм Флада. Вычтем из всех элементов каждой строки минимальный элемент этой строки. Из элементов первой строки вычитаем 0, второй – 1, третьей – 4 и т.д.:

5  3  0  710

В полученной матрице вычтем из всех элементов каждого столбца минимальный элемент этого столбца. Из элементов первого столбца вычитаем 1, второго, третьего и четвёртого – 0, пятого – 6:

В результате мы получили матрицу, содержащую допустимое решение задачи. Проверяем его на оптимальность, для чего зачёркиваем минимальным числом прямых вертикальных и/или горизонтальных линий все имеющиеся в матрице нули:

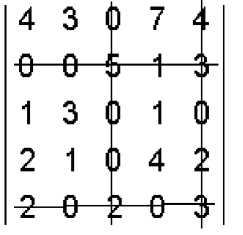
Поскольку число прямых, использованных для вычёркивания нулей, меньше n=5, полученное решение не является оптимальным. Чтобы его улучшить, среди незачеркнутых элементов матрицы оценок выбираем минимальный элемент (в данном случае он равен 1), вычитаем его из всех незачеркнутых элементов и прибавляем ко всем элементам, зачеркнутым дважды. После этого проверяем улучшенное решение на оптимальность:

3 2 I) 6 4

О 0 6 14

- 0 0 3 2

Теперь число прямых, необходимых для зачёркивания всех нулей, равно 5, следовательно, получено оптимальное решение.

Сформируем матрицу искомых переменных

| xij |=

Таким образом, первого кандидата следует назначить на 3-е рабочее место, второго – на 1-е, четвёртого – на 2-е, пятого – на 4-е. В этом случае суммарная производительность окажется максимальной и составит Z= ΣСij∙xij =10·1+8·1+7·1+9·1=34. Третьего кандидата, закреплённого за фиктивным рабочим местом, брать на работу нецелесообразно.