Оптимальное размещение погрузочных пунктов вдоль лесовозного уса

Положение лесовозного уса на лесосеке определяет величину затрат на трелевку лесоматериалов и их перевозку по лесовозной ветке. Для снижения себестоимости заготовки древесины в узких лесосеках ус целесообразно прокладывать по краю лесосеки со стороны магистрали, а в широких лесосеках смещать его от середины лесосеки в сторону магистрали на некоторое расстояние, определяемое из условия минимизации затрат на перевозку древесины по ветке и трелевку лесоматериалов.

В работах [5], [6] смещение уса по направлению грузопотока по ветке установлено без учета изменения расстояний между погрузочными пунктами, которое зависит от среднего расстояния трелевки. В работе [6] не рассмотрен вариант примыкания трелевочных волоков длинных и коротких пасек под разными углами. Смещение уса в сторону магистрали приводит к образованию на лесосеке ряда коротких пасек (со стороны магистрали) и ряда длинных пасек (со стороны границы зоны тяготения магистрали). Если ус примыкает к ветке под углом а , то при трелевке лесоматериалов тракторами и валочно-трелевочными машинами целесообразно следующее размещение трелевочных волоков [5], [6]: магистральные волоки расположены вдоль уса, пасечные волоки со стороны магистрали (в коротких пасеках) размещаются перпендикулярно усу, а пасечные волоки со стороны границы зоны тяготения магистрали (в длинных пасеках) размещаются под углом а к усу или параллельно направлению ветки (рис. 1а); пасечные волоки расположены параллельно усу, магистральный волок со стороны магистрали (в коротких пасеках) размещается перпендикулярно усу, а магистральный волок со стороны границы зоны тяготения магистрали (в длинных пасеках) - под углом а к усу или параллельно направлению ветки (рис. 1б).

Предложенное размещение трелевочных волоков в пасеках обусловлено сокращением рас- ходов на трелевку лесоматериалов. Идеализированная форма лесосеки при таком размещении волоков деформируется, и ее часть со стороны границы зоны тяготения магистрали имеет форму параллелограмма, а со стороны магистрали -прямоугольную. Когда ус примыкает к ветке под прямым углом, пасечные и магистральные волоки в коротких и длинных пасеках размещаются одинаково.

Оптимальное расстояние между погрузочными пунктами определяется по минимуму суммарных удельных затрат zcy (в рублях на кубический метр) на устройство погрузочного пункта и трелевку древесины к этому погрузочному пункту [3], [4], [7]. Целевая функция имеет вид zCy = СПП + z МВ + znB ^ min, (1) q где сПП - затраты на устройство, содержание и ликвидацию погрузочного пункта, руб.; zMB - затраты на устройство магистральных трелевочных волоков и на трелевку древесины по ним, руб.; znB - затраты на устройство пасечных трелевочных волоков и на трелевку древесины по ним, руб.; q - объем заготавливаемой древесины в пасеке - объем вывозки с погрузочного пункта, м3.

^ZMB = C MB l MB + lCMB b MB q O + ¹см ^Ь м ^qn , (2) где С МВ - удельная стоимость устройства магистрального волока, руб./км; 1 МВ - протяженность магистрального волока в пасеке, км; 1 СМВ - среднее расстояние трелевки по магистральному волоку при основных работах, км; Ь МВ - стоимость трелевки по магистральному волоку при основных работах, руб./(м³ • км); q O - объем трелевки древесины при основных работах, м³; 1_С М - среднее расстояние трелевки по магистральному волоку при подготовительных работах, км; Ь М -стоимость трелевки по магистральному волоку при подготовительных работах, руб./(м³ • км);

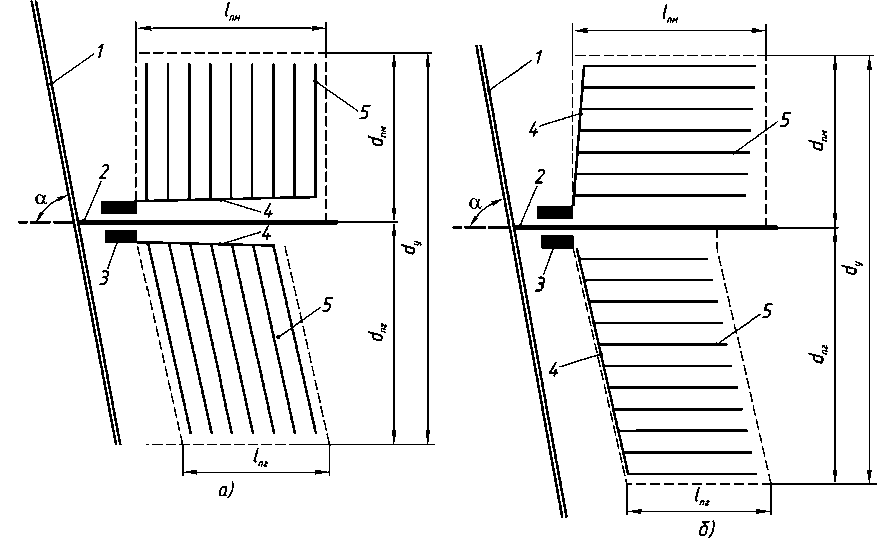
Рис. 1. Схемы размещения трелевочных волоков и погрузочных пунктов относительно лесовозного уса:

1 – лесовозная ветка; 2 – лесовозный ус; 3 – погрузочный пункт; 4 – магистральный трелевочный волок; 5 – пасечный трелевочный волок; а – магистральные волоки расположены вдоль уса; б – пасечные волоки расположены вдоль уса

q_П – объем трелевки древесины при подготовительных работах, м³.

^ZПВ   C nB l nB + ¹СПВ^ЬПВ q o + ^lcn b n q n ,     (3)

где С_ПВ – удельная стоимость устройства пасечного волока, руб./км; l_ПВ – протяженность пасечных волоков в пасеке, км; l_СПВ – среднее расстояние трелевки по пасечным волокам при основных работах, км; b_ПВ – стоимость трелевки по пасечным волокам при основных работах, руб./(м³ ⋅ км); l_СП – среднее расстояние трелевки по пасечным волокам при подготовительных работах, км; b_П – стоимость трелевки по пасечным волокам при подготовительных работах, руб./(м³ ⋅ км).

Целевая функция (1) и ее составляющие, определяемые по зависимостям (2) и (3), включают параметры, которые зависят от принятого технологического процесса лесосечных работ ( с_ПП , b_МВ , b_ПВ , b_П ) и размеров пасеки ( l_МВ , l_ПВ , q , l_СПВ , l_СП, q_ПВ , q_П ). Примем, что пасека имеет следующие размеры (в километрах): l_П – ширина пасеки (расстояние между погрузочными пунктами); d_П – длина (глубина) пасеки – расстояние по нормали от лесовозного уса до границы пасеки.

Для того чтобы найти оптимальную ширину пасеки l_П , надо взять производную от z_СУ по l_П и, приравняв ее к 0, решить полученное уравнение относительно l_П . Найдем производную и приравняем ее к 0. Получаем

ет форму параллелограмма. При равномерном распределении запаса ликвидной древесины по площади лесосеки объем заготовки древесины на пасеке q составит q _ 100/д 1п dп , (6) где γЛ – ликвидный запас древесины на лесосеке, м3/га.

Из формулы (6) можно найти, что q/= 100 γЛdП. Подставим выражения, определяющие q и q/ , в уравнение (5) и, выполнив его преобразование с учетом того, что сПП = const, получим l f d^ +

П I dl n

dz । dzПВ

77 I ^СПП + ^ZMB + ^ZnB . di n I

dz cy _ ^{( С} ПП + ^Z MB + z nB ) q q ^{( С} ПП + ^Z MB + ^z ПВ dl П                        q ²

_ 0. (4)

Так как объем заготовки древесины на пасеке не равен 0, то q ² ≠ 0, следовательно,

^{( С}ПП + ^ZMB

+ ^ZПB ) q ^_ q ^{( С}ПП

+ ^ZMB

+ ^ZПB ) .

При примыкании уса к ветке под некоторым углом α , как было сказано ранее, пасека име-

Для решения уравнения (7) требуется определить затраты z_МВ и z_ПВ в зависимости от параметров пасеки и технологического процесса лесосечных работ и их производные.

Протяженность трелевочных волоков и средние расстояния трелевки зависят не только от размеров пасеки, но и от расположения волоков. При размещении магистрального волока вдоль уса (рис. 1а) его протяженность в пасеке lMB _ kPM I a0 + ln : |, (8) V sin a )

где k_РП – коэффициент удлинения магистрального волока; a ₀ – протяженность магистрального волока за пределами пасеки, км; a_К – расстояние от конца магистрального волока до границы пасеки, км.

Среднее расстояние трелевки по магистральному волоку будет одинаковым как при основных, так и при подготовительных работах, то есть l_СМВ = l_СМ . Величину l_СМВ определим из условия равномерного распределения запаса древе-

сины на пасеке и того, что форма пасеки близка

к правильной:

1СМВ Ррм

Возьмем производную от функции (15):

a 0 + 0,5 I i

sin а

Подставим зависимости (8) и (9) в формулу (2) с учетом, что q_O = 100 γ_Пl_П ( d_П – s ), q_П = 100 γ_Пl_Пs , и выполним преобразования

dz dzПВ kpn din

CnB ( dn an SMB aS ) + a bnB ( d n — s )( d n ~a— ~s )

^{+ 50} Y

sin а

_⁺ b n ^{( S — S} MB ^{)( S — S} MB

aS ) _

aК sin а

z MB  ^kPM ‘

+ 50 / л I n I 2 a 0 ^—

a V b MB ( d n ^{— s} ) ⁺ b M s ]4 , (10) sin а /-                 ^J

⁺ 5° У Л I n [ b MB ⁽ d n s ^{) +} b M s

где s – расстояние от оси уса до бровки магистрального волока, км.

dz™   ,    C MB ^{+ 50} У л I ² a 0         |[ b MB ( d n s ^{) +} b M s ]

= ^kPM -j            V ^{sin а} )                   ^J

^{+ 100} Х л l n [ b MB ^{( d}n ^{— S ) +} b M s J

L . (11)

Протяженность пасечных волоков lПВ определяется как произведение количества волоков в пасеке, равное lПsinα/a, на протяженность волока, которая составляет (dП – aП– s)/sinα, где a – ширина зоны тяготения к пасечному волоку, км; aП – расстояние от конца пасечного волока до границы пасеки, км. Следует также учесть прокладку пасечных волоков в зоне между лесовозным усом и магистральным волоком; при размещении этих пасечных волоков перпендикулярно магистральному волоку их количество составит lП / a, протяженность волока (s – sМВ – aS), где sМВ – ширина магистрального волока, км; aS – расстояние от конца пасечного волока до оси уса, км. На основе вышеизложенного получаем kl lnB = a (dn — an — sMB — as),        (12)

где k_РП – коэффициент удлинения пасечного волока.

Среднее расстояние l_CПВ и объем q_CПВ трелевки древесины по пасечным волокам равны: l cnB = ^{kpn (} dⁿ. a ^{n s} ) ; q o = ¹⁰⁰ / л l n ( ^dn ^{— s} ) . (13) 2sin а

Среднее расстояние l_CП и объем q_П трелевки древесины по пасечным волокам при подготовительных работах составляют:

l cn = 0,^{5 k}pn ^{( S — S}MB ^{— a}s ) ; q n = ¹⁰⁰ 7 л l n ^{( S — S}MB ) -(14)

Подставим выражения (12)–(14) в формулу (3):

^C nB ^{( d} n ^— a n ^{— S} MB ^— a S ) +

a

z nB    ^k pn l n ^<

b nB ^{( d} п ^{s )( d} п ^a n ^s )     "  . (15)

^{+ 50} Y

sin а

_⁺ b n ^{( S — S} MB ^{)( S — S} MB

aS ) 1

L . (16)

Совместный анализ формул (15) и (16) позволил установить, что z_ПВ = l_Пdz_ПВ / dl_П . С учетом этого уравнение (7) можно упростить:

dz zМВ

ПdlП

= c nn ⁺ z MB .

Подставим выражения (10) и (11) в уравнение (17) и произведем его преобразование. Решение уравнения (17) при подстановке зависимостей (10) и (11) и с учетом, что l_П > 0, имеет вид

i n = 0,14

c nn ^{sin а + k}P*M c mb ( a 0 ^{sin а} a K )

У ГлkPM _bMB ( dn — s ) + bMs] sin а

. (18)

При примыкании уса к ветке под прямым углом ( α = 90°), sin α = 1 формула (18) примет вид

i n = 0,14

• nn ^{+ k}PM c mb ⁽ a 0 ^aK )

\ Ул ^kPM _ b MB ^{( d} n ^{s ) +} b M ^s J

При одинаковых затратах на трелевку при основных и подготовительных работах ( b_МВ = b_М ) формулы (18) и (19) примут вид

i n = 0,14

i n = 0,14

У л ^kPM b MB^dn ^{sin а}

c nn ^{sin а + k}P'M C MB ( a 0 ^{sin а}

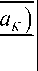
c nn ^{+ k}PM C MB ⁽ a 0 a К )

У л k P'M ^bMB^d n

В известных формулах для определения расстояния между погрузочными пунктами [1], [2], [3], [4], [7] параметры a ₀ и a_k не учитывали. Если принять a ₀ = a_k или a ₀ = a_k = 0, то формула (19) еще упростится. Получаем известную зависимость [2], [3], [4], в которой d_П = d_У / k_ПУ .

На рис. 2 представлены графики зависимостей l_П = f ( d_П ) при углах примыкания уса к ветке 60° и 90 ^П °. Угол 60° принят из условия, что ус располагается параллельно направлению грузопотока по магистрали, а стоимость вывозки по магистрали b_М составляет половину от стоимости вывозки по ветке b_В . Оптимальный угол примыкания ветки к магистрали [7] составляет cos α = b_М / b_В . При принятом условии, что b = 0,5 b , cos α = 0,5 соответственно α = 60°.

МВ

Из рис. 2 видно, что оптимальное расстояние между погрузочными пунктами l_П при размещении магистрального волока вдоль лесовозного уса убывает с возрастанием глубины пасеки d_П , причем при небольших значениях глубины пасеки ( d_П = 100…200 м) убывание наиболее

интенсивное. Уменьшение ликвидного запаса древесины приводит к возрастанию расстояния между погрузочными пунктами. Сравнение рис. 2а и 2б показывает, что влияние угла примыкания уса к ветке на расстояние между погрузочными пунктами несущественно. При угле примыкания 60° указанное расстояние больше всего на 2…3 м, чем при угле примыкания 90°. Если к усу примыкают две пасеки глубиной соответственно 200 и 300 м, то разница в расстояниях между погрузочными пунктами, располагаемыми по разные стороны от уса, составит более 30…50 м.

При размещении пасечных волоков вдоль уса (рис. 1б) протяженность магистрального волока в пасеке l_МВ составит

f d П — a К — 5 | l-мв = крм I a о + : I, (22) V sin a )

где s – расстояние от оси лесовозного уса до границы зоны безопасности, км.

Среднее расстояние трелевки по магистральному волоку l_СМВ определим исходя из тех же условий, что и для формулы (9). Оно составляет

f dn — a„ — 5 |

ПК

CMB PM I a 0 ⁺ ~ ■          I ^{.           (23)}

V 2sin a )

dZ M^ = Ю0 г _л к рм Ь мв IT a 0 + d" a^{K 5} 1 ( d n ~ 5 ) + a 0 5 1 . (25) dl "                LV 2 sin a )

Пользуясь формулами (24) и (25), получаем

„    1 dzMB_ = k r f     dП — aK — 5 I zMB П            РМ MB I a0 +      •          |. ( )

dl n          V        sin a )

С учетом зависимости (26) уравнение (7) примет вид dz

ПВ

П       cnn + z"B dlП

^{+ k}PM C MB I a 0 ⁺

d n — a к — 5 sin a

Протяженность пасечных волоков lПВ зависит от глубины пасеки dП и ее ширины lП. Пользуясь схемой рис. 1б, можно установить, что l"B = -^П-^- (ln — an — 5MB ). (28)

Среднее расстояние трелевки по пасечным волокам при основных и подготовительных работах будет одинаковым (lСПВ = lСП) и составит lcnB = 0,5kPn ( ln — an — 5MB ). (29)

Подставим формулы (28) и (29) в выражение (3). Выполнив преобразование, получим

Подставим полученные зависимости (22) и (23) в формулу (2), при этом учтем, что среднее расстояние трелевки, определяемое по формуле (23), соответствует объему древесины q_O , а объем q_П имеет расстояние трелевки a ₀. После преобразований имеем

7. _ zMB  Рмм

d_n — a_K — 5

ПК

I a 0 +-

V sin a )

f .(24)

+100r^ bMBli dПCПВ znB    Pn (41 an 5MB )]

1 a(30)

⁺ 50Y Л l n L b nB ^{( d}n ^{— 5} ) ⁺ b n⁵ ] [ •

Производная от функции (30) имеет вид dZnB = kpn I dnCnB. + 50Ул L bnB (d п — 5 ) + dlnI

+ bn51 (2ln — an — 5MB ) ( .

a 0 ⁺ d" a^{K 5} | ( d П ^{— 5} ) ⁺ a 0 ⁵

2sin a )

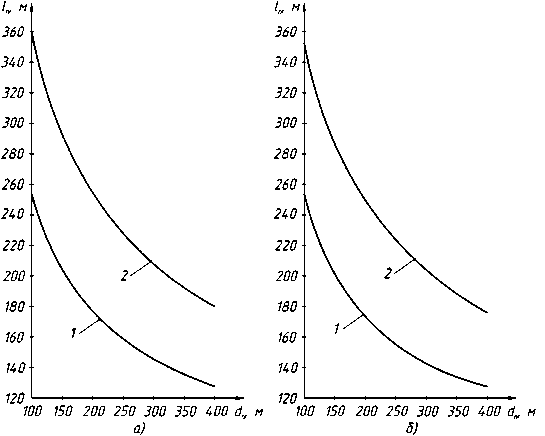
Рис. 2. Графики зависимости оптимального расстояния между погрузочными пунктами от глубины пасеки при размещении магистрального волока вдоль уса: 1 - Y_Л 200 м³/га; 2 - Y_Л = 100 м³/га; а - а = 60 ° ; б - а = 90 °

Для нахождения зависимости, определяющей оптимальное расстояние между погрузочными пунктами, формулы (30) и (31) подставляем в уравнение (27). Решая полученное уравнение относительно аргумента l_П , имеем

I n = 0,14

' ПП a d П ^С ПВ ^к РП ( a n + s МВ ) + ¹ МВ ^C МБ a У л k pn a [ ^Ьпв ⁽ d n - s ) + b n s J

. (32)

В формуле (32) протяженность магистрального волока l_МВ определяется по зависимости (22), которая при примыкании уса к ветке под прямым углом ( α = 90°, sin α = 1) имеет вид

¹МБ = ^kРМ ⁽ a 0 + d n - ^aK - s ) . ⁽³³⁾

Когда затраты на трелевку при основных и подготовительных работах одинаковые ( b_ПВ = b_П ), формула (32) выглядит следующим образом:

l n = 0,14

c nn a d n C nB ^k pn ⁽ a n + ^S MВ ) + ¹ М^Б ^С МБ a У л ^k pn ab nB d n

. (34)

Формулы (34) и (32) в совокупности с выражениями (22) и (33) показывают сложную зави- симость оптимального расстояния между погрузочными пунктами от глубины пасеки при размещении пасечных волоков вдоль уса. Для представления указанной зависимости построены графики зависимостей lП = f(dП) при углах примыкания уса к ветке 60° и 90° (рис. 3).

Оптимальное расстояние между погрузочными пунктами l_П при размещении пасечных волоков вдоль лесовозного уса убывает с возрастанием глубины пасеки d_П , убывание наиболее интенсивное при небольших значениях глубины пасеки ( d_П = 100…200 м). Уменьшение ликвидного запаса древесины приводит к возрастанию расстояния между погрузочными пунктами. Сравнение рис. 3а и 3б показывает, что влияние угла примыкания уса к ветке на расстояние между погрузочными пунктами несущественно. При угле примыкания 60° указанное расстояние больше всего на 4…6 м, чем при угле примыкания 90°. Если к усу примыкают две пасеки глубиной 200 и 300 м, разница в расстояниях между погрузочными пунктами, располагаемыми по разные стороны от уса, составит 27…38 м в зависимости от ликвидного запаса древесины, или 16 %.

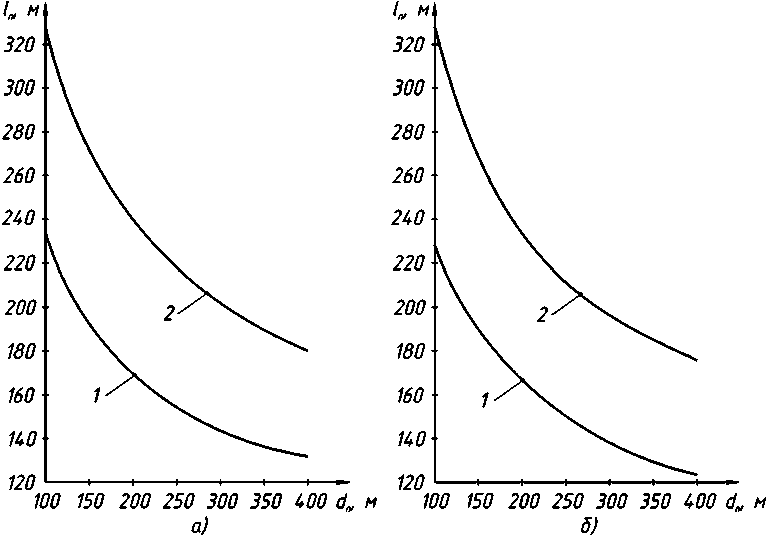
Рис. 3. Графики зависимости оптимального расстояния между погрузочными пунктами от глубины пасеки при размещении пасечных волоков вдоль уса: 1 - Y_Л 200 м³/га; 2 — Y_Л = 100 м³/га; а — а = 60 ° ; б - а = 90 °