Оптимальное размещение средств компенсации реактивной мощности с помощью метода дифференциальной эволюции

Традиционно мероприятия, связанные с регулированием перетоков реактивной мощности в распределительных сетях, позволяют решить широкий спектр задач, связанных с обеспечением надежного электроснабжения потребителей и повышения энергоэффективности систем. В распределительных сетях компенсация реактивной мощности подразумевает необходимость её дополнительной инъекции в определенных точках сети. В частности, установка средств компенсации реактивной мощности (СКРМ) на секциях шин, к которым подключены крупные асинхронные двигатели или их группы, обеспечивает полностью или частично потребность этих машин в реактивной мощности и оказывается, как правило, эффективной, поскольку исключает тем самым отрицательные факторы от протекания этой мощности от питающей сети к отдельным установкам потребителей. Озвученная эффективность заключается в достижении следующих целей в управлении режимом сети: поддержание нормируемой величины tg φ, ограничение токовой загрузки кабельных (КЛ) и воздушных линий (ВЛ) (снижение аварийности в распределительной сети, например, за счет снижения температуры кабельных линий и, как следст- вие, замедления старения их изоляции [1]), снижение потерь электроэнергии, поддержание требуемого уровня напряжения (уменьшение накопительного экономического ущерба [2] и ограничение риска нарушения устойчивости двигательного оборудования [3]).

Учет перечисленных факторов, определяющих целесообразность установки СКРМ, совместно с осуществлением выбора точек подключения и мощности этих устройств, анализом нормальных и аварийных режимов работы сети, а также оценкой затрат на реализацию проекта составляют комплексную задачу оптимизации размещения компенсирующих устройств.

Научным сообществом вводятся различные постановки этой задачи нелинейного программирования [4, 5] и смежных с ней [6]. При этом, несмотря на то, что в качестве расчетных инструментов рядом исследователей предлагаются детерминистические методы [7] или методы нейронных сетей [8], сегодня значительная доля научных публикаций по теме посвящена оценке эффективности применения в этой области различных метаэври-стических подходов. Так, в работе [9] предлагается методика распределения подлежащей компенсации реактивной мощности в радиальных сетях на основе генетического алгоритма оптимизации. Генетический алгоритм также используется в исследовании [10], где применяется для оптимизации состава и мест подключения регулируемых батарей статических конденсаторов (БСК) в крупномасштабных сетях электроснабжения. Авторы работы [11] описывают алгоритм оптимального размещения статических СКРМ с учетом режима сети и ограничений на уровни напряжения в её узлах с помощью метода химических реакций. Исследование [12] демонстрирует перспективную результативность применения двухэтапного подхода к оптимальному размещению СКРМ: на первом шаге с помощью индексов чувствительности величины потерь определяются наилучшие точки подключения устройств; на втором на базе алгоритма муравьиной колонии производится выбор мощности отдельных вводимых установок и уточняется их положение. Говоря об альтернативной постановке задачи оптимизации, следует упомянуть работы группы авторов, предлагающих [5, 13] процедуру, нацеленную на максимизацию показателей надежности сети электроснабжения, и использующих для этого метод светлячков. Наконец, в работе [14] для решения задачи оптимального размещения БСК в системе электроснабжения используется метод роя частиц, эффективность которого здесь же сопоставляется с разновидностями генетических алгоритмов и поиска с запретами.

Несмотря на активность исследований в рассматриваемой области, для всех перечисленных работ характерен ряд допущений. Во-первых, затраты на установку СКРМ рассчитываются исходя из удельной стоимости на кВар мощности ($/кВар), либо исходя из стоимости отдельного конденсатора, как составной части БСК, что позволяет лишь приблизительно оценить предполагаемые затраты. На самом деле стоимость отдельных устройств нелинейно зависит от их мощности, что при принятии упомянутого допущения приводит к чрезмерно оптимистичной оценке затрат в ходе оптимизации. Во-вторых, в большинстве работ не принимаются во внимание уже имеющиеся в сети возможности регулирования режима, например, РПН понижающих трансформаторов и переключение отпаек регулируемых БСК. Наконец, в-третьих, в рамках одной процедуры не учитывается возможность оптимального размещения разнотипных СКРМ – речь всегда идет либо о БСК, либо о статических компенсаторах и т. д.

Как результат, вытекающий из вышеизложенного, в данной статье предлагается методика вы- бора подключаемых в точках сети СКРМ из подготовленного расчетчиком перечня моделей разнотипных устройств с применением метода дифференциальной эволюции (ДЭ), учитывающая существующие возможности регулирования режима, реализованная на базе программного комплекса (ПК) DIgSILENT PowerFactory [15]. Применяемый метод ДЭ, предложенный Метрополи-сом (Metropolis N.) [16] и впоследствии развитый Сторном (Storn R.) [17] – это метаэвристический алгоритм, основанный на использовании векторных операций суммирования при выполнении избирательной процедуры скрещивания в множестве возможных решений, элементы которого итерационно приближаются к глобальному оптимуму пространства состояний задачи. Этот эволюционный подход показал свою эффективность при решении целого спектра технических задач и в частности при оптимизации маршрутов прокладки инженерных сетей [18], управлении состоянием асинхронных двигателей [19], планировании ремонтов генерирующего оборудования энергосистем [20].

Постановка задачи оптимального размещения СКРМ

Задача. Выбрать оптимальный вариант вводимого устройства СКРМ для каждой из точек множества потенциальных узлов подключения N, заданного расчетчиком.

Критерий. Максимальный чистый дисконтированный доход с учетом затрат на установку СКРМ и экономического эффекта от изменения потерь электроэнергии за период T , а также требования обеспечения допустимых уровней напряжения V_k Е [V™ⁱⁿ; V™^ax] в каждом из контролируемых узлов b = 1, ..., В.

Варьируемые переменные. Номера строк таблицы моделей устройств х = (х₁,х₂, — ,x_N,x_l Е Ы) для каждого из целевых узлов N. В качестве примера в табл. 1 представлен шаблон исходных данных, необходимых для выполнения процедуры оптимального размещения регулируемых БСК. В табл. 1 q₀ - реактивная мощность, соответствующая одному шагу регулирования БСК, Мвар; а₀ - число шагов регулирования БСК; М(х₁) - капиталовложения в установку БСК соответствующей модели.

Первая строка табл. 1 соответствует случаю, при котором в узле i не вводится новое оборудование; все остальные – определяют характеристики оборудования и капиталовложения на год реализации проекта. Представленный формат позво-

Таблица 1

Шаблон таблицы моделей для размещения регулируемых БСК

Xl Тип устройства Поле № 1 q0 Поле № 2 а0 М(Х[), тыс. руб. 1 0 0 0 – 0 2 БСК (рег.) 0,100 4 – 250 ляет в рамках одной таблицы объединять различные типы устройств и рассматривать их в рамках одной процедуры совместно как альтернативные решения. В частности, когда в качестве альтернативы БСК рассматривается возможность установки, например, синхронного компенсатора реактивной мощности, в табл. 1 нужно добавить строку х, = 3, для которой определить в следующих столбцах 3 поля: Vset - заданное напряжение в целевом узле, кВ; Qmax и Qmin — максимальный и минимальный пределы мощности компенсатора; М(х,) - капиталовложения в установку.

Математический метод. Метод ДЭ [16, 17].

Целевая функция. В соответствии с критерием оптимизации ЦФ задачи выбора СКРМ ф(х) включает в себя чистый дисконтированный доход h(x) и штрафную составляющую р(х), учитывающую выполнение ограничений на уровни напряжений в целевом множестве контролируемых узлов b:

ф(х) = h(x) - р(х) =

= h⁽x) - Eg^i С д Н д (х) ^ max, (1) где ф(х) - целевая функция оптимизации решаемой задачи; р(х) - штрафная функция, нулевое значение которой соответствует отсутствию нарушений заданных ограничений; п_й - расчетная величина, характеризующая степень нарушения ограничения d для рассматриваемой версии плана ремонтов; с_й - коэффициент составляющей штрафной функции, масштабирующий нарушения к единицам целевой функции.

Экономическая составляющая h(x) ЦФ (1) включает в себя дисконтированные затраты на установку оборудования за расчетный период T и экономический эффект – изменение платы за электрическую энергию (ЭЭ) вследствие корректировки потерь с учетом дисконтирования:

h(x) = П=1 р. '1 - К(х), (2)

где К(х) - общие капиталовложения в установку всех планируемых СКРМ в соответствии с вариантом х в узлах I = 1, ^,N за расчетный период [21]:

К(х)=1^К(х₁) = ^Vj^Mi^+VL i^^ )^

= I'Ll (am/x,) + ^ах^), (3) где Pt - обобщенный коэффициент доп. затрат для устройства i, зависящих от условий проведения работ, региона доставки оборудования и пр.; Mi(xi) - исходная стоимость устройства СКРМ i, отнесенная к году проведения работ (первому году расчетного интервала), тыс. руб.; Е - ставка дисконтирования; It - эксплуатационные издержки в год t, тыс. руб.; « - доля издержек на ремонты, обслуживание и амортизационные отчисления от исходной стоимости устройства СКРМ i; mt - тариф на ЭЭ в год t расчетного периода, тыс. руб./МВт^ч; ДLt(x) - потери ЭЭ при установке СКРМ согласно варианту х для года t расчетного периода, рассчитываемые по выражению

ДLt(x) = ДР™гр(х) X Tmax +

+ДР™(х) X 8760, (4) где ДР,^нагр(х) и ДР™(х) - соответственно нагрузочные потери и потери холостого хода в сети в максимальном режиме в год t расчетного периода, МВт; T_max - число часов максимума потерь мощности, рассчитываемое согласно одной из общепринятых методик [22, 23]; ДЬ ° - потери ЭЭ в исходной схеме без СКРМ для года t расчетного периода, МВт·ч. Последняя величина рассчитывается по выражению (4), либо предопределяется расчетчиком в исходных данных.

В качестве ограничений в представленной постановке задачи оптимального размещения СКРМ учитываются следующие два: обеспечение минимального и максимального предельных уровней напряжения л^^т1п и л^^тах соответственно в контролируемых узлах В для схемно-режимных ситуаций 5:

л^т1п(х) = -х

/V- Vх утах;ТЬ-'п V. ;х)лш'. (5)

Лгтах(х) = ix х EU Р CkV. ^ - Vbmax; 0))2, (6) где Vbmin - заданный минимальный предельный уровень напряжения в узле b, кВ; Vbmax - заданный максимальный предельный уровень напряжения в узле b, кВ; Vb,^(х) - расчетное значение напряжения в узле b в схемно-режимной ситуации s, кВ. Фактически ограничения (5) и (6) учитывают требования, предъявляемые к величинам напряжений в узлах b, как среднее по 5 рассматриваемым режимам суммарное нарушение заданных максимальных и минимальных уровней параметра для каждого узла b.

Схема расчета ЦФ и интеграция с ПК DIgSILENT PowerFactory. Для расчета таких величин, как Vb,s(x), Дрнагр(х) и ДР,хх(х), необходимо выполнение расчета установившегося режима (УР) с использованием цифровой модели исследуемой системы. Кроме того, необходимо также учитывать все имеющиеся доступные средства для введения режима в допустимую область. Для решения этой задачи возможно применение стороннего программного обеспечения, позволяющего выполнять соответствующие расчеты, и реализация на его базе предлагаемого алгоритма в виде подпрограммы. В представленном исследовании в качестве такого программного комплекса используется ПК DIgSILENT PowerFactory, который позволяет без дополнительных расчетных процедур выполнить расчет УР с учетом автоматического РПН трансформаторов, переключения отпаек регулируемых БСК, группового регулирования реактивной мощности синхронных машин. В связи с этим алгоритм расчета ЦФ принимает следующий вид.

Входные данные: номера строк таблицы моделей устройств х = {x₁,x₂, .„,x_N,x_t Е Ы), для которых должна быть рассчитана ЦФ (1).

Шаг 1: по формуле (3) рассчитываются общие капиталовложения в установку всех планируемых СКРМ К(х)

Шаг 2: в ПК DIgSILENT PowerFactory производится расчет режимов максимального потребления для каждого года t расчетного периода T при исходной схеме сети и с учетом установки СКРМ х. Результат расчета – нагрузочные потери и потери холостого хода в сети для каждого года t – Д/Д^агр(х) и ДР_£^хх(х).

Шаг 3: рассчитывается составляющая ЦФ Д(х) по формуле (2).

Шаг 4: в ПК DIgSILENT PowerFactory производится расчет режимов максимального потребления для каждой предварительно заданной схемнорежимной ситуации s, в которой должны выполняться ограничения задачи, и с учетом установки СКРМ х. Результат расчета - уровни напряжений в контролируемых узлах b - Ц,,_х(х).

Шаг 5: рассчитывается штрафная составляющая ЦФ р(х) по формуле (1).

Шаг 6: рассчитывается полная ЦФ ф(х) по формуле (1).

Выходные данные: значение ЦФ ф(х) для набора устройств х.

Процедура метода ДЭ представлена в следующем разделе.

Допущения. В постановке задачи и последующих расчетах приняты следующие допущения.

• 1.    Задача выбора потенциальных узлов для установки СКРМ считается независимой и решаемой предварительно. Наличие в таблице 1 первой строки, которой соответствует отсутствие СКРМ в узле i, позволяет расчетчику принимать в качестве возможных мест установки заведомо большее количество узлов сети, часть из которых отсеется в ходе расчета.

• 2.    Все капиталовложения в установку устройств относятся к первому году реализации проекта.

• 3.    При расчете платы за потери учитывается только тариф за ЭЭ, но не учитывается плата за мощность в часы/плановые часы пиковой нагрузки.

• 4.    При расчете потерь не учитываются аварийные и ремонтные режимы.

• 5.    В стоимость не включены затраты на сооружение новых ячеек – в тестовых расчетах предполагается наличие резервных присоединений.

Введенные допущения могут быть разрешены в дальнейшем и не оказывают значительного влияния на результат или во всяком случае не приводят к чрезмерно оптимистичным оценкам вариантов устанавливаемых СКРМ.

Метод ДЭ в задаче оптимальногоразмещения СКРМ

Алгоритм работы метода ДЭ можно представить в виде следующей последовательность действий.

• 1.    С помощью случайного равномерного рассеивания в допустимом диапазоне значений гене-

• рируется начальное множество вариантов установки СКРМ х,. Эти вектора составляют популяцию - матрицу Р, столбцы которой являются векторами х, возможных комбинаций устройств СКРМ.

• 2.    Последовательно для каждого элемента популяции х, случайным образом выбираются два других вектора х_а и х_ь. Далее производится рас

• 3.    Путем случайного замещения части варьируемых переменных Хц вектора х, переменными вновь полученного промежуточного вектора г определяется перспективный элемент популяции и. Если ф(и) <  ф(х , ), то вектор-потомок и замещает вектор х, в множестве возможных решений Р. Если ф(и) >  ф(х , ) - вектор и отбрасывается.

• 4.    Шаги 2 и 3 повторяются до тех пор, пока не будет выполнено одно из следующих условий:

  • 4.1.    На протяжении k_lim1 итерационных расчетов лучшее найденное значение целевой функции в популяции остается постоянным (популяция остановилась в развитии).

  • 4.2.    Достигнуто предельное число итераций расчета k_Um2 .

чет вспомогательного вектора г:

'-Й-                   (7)

^nJ     LxnjJ         |^Lxn,aJ    Lxn,bJJ где 9 - коэффициент скрещивания. Если один или несколько элементов вектора г выходят по результатам расчета за допустимые пределы (например, г, < 0, что с точки зрения решаемой задачи невозможно, поскольку индексация строк начинается с 1), то эти элементы приравниваются к ближай- шему граничному значению диапазона.

Нельзя оставить без внимания вопрос, касающийся целочисленности варьируемых переменных Хц. С учетом того что коэффициент скрещивания, как правило, находится в пределах интервала 9 Е (0; 1), при выполнении процедуры скрещивания (7) элементы результирующего вспомогательного вектора г оказываются нецелыми числами. В таком случае перед расчетом ЦФ на шаге 3 алгоритма ДЭ все координаты векторов х , и и округляются до ближайших целых.

Методика эксперимента и тестовая модель

Анализ эффективности работы предлагаемого алгоритма размещения СКРМ производится на основании результатов вычислительного эксперимента на базе модифицированной тестовой 14-узловой схемы IEEE (IEEE14).

В рамках расчета выполняется процедура оптимального размещения СКРМ в сети 33 кВ модели IEEE14 с учетом экономического эффекта от минимизации потерь в сети 33 кВ и поддержания напряжений в этой же сети в диапазоне ±7,5 % для всех отказов по критерию п — 1. Исходные данные модели IEEE14 находятся в открытом доступе [24].

Поскольку исходный режим сети IEEE14, смоделированной в ПК DIgSILENT PowerFactory, не требует оптимизации (в сети 33 кВ уже установлена большая по мощности БСК), а также не принимаются во внимание пределы реактивной мощности синхронных компенсаторов и генерирующего оборудования, в исследовательских целях модель была скорректирована по нескольким пунктам.

• 1.    Выведен из работы емкостной шунт в узле № 9.

• 2.    Величина энергопотребления в узлах сети 33 кВ увеличена на 20 %.

• 3.    Величина энергопотребления в узлах сети 132 кВ увеличена на 10 %.

• 4.    При расчете УР в ПК DIgSILENT PowerFactory учтены пределы по активной и реактивной мощности синхронных машин.

• 5.    При расчете УР в ПК DIgSILENT PowerFactory автоматически выполняются РПН трансформаторов и выбор отпаек устанавливаемых БСК по критерию поддержания напряжения в узле подключения.

В табл. 2 приводится перечень моделей, из которых формируется комбинация подключаемых на классе 33 кВ устройств. В расчетном примере для наглядности рассматриваются только альтернативы установки различных моделей БСК. Возможность совмещённого выбора различных типов устройств описана при постановке задачи и до- полнительной проверки не требует. Параметры БСК (номинальная мощность, число отпаек) взяты из открытых источников производителей для линейки устройств 35 кВ [25, 26].

Коэффициент дополнительных затрат (3) принят одинаковым для всех устройств ^ = ^ = 1,232; доля издержек на ремонты, обслуживание и амортизационные отчисления - а = 0,094; ставка дисконтирования Е = 0,05. Цены на оборудование установлены в соответствии с Приказом Министерства энергетики РФ от 17 января 2019 г. № 10 «Об утверждении укрупненных нормативов цены типовых технологических решений капитального строительства объектов электроэнергетики в части объектов электросетевого хозяйства» и приведены к 2020 году, исходя из предположения о величине ежегодной инфляции 5 %. Расчетный период для экономической оценки проекта Т = 5 лет. Тариф на ЭЭ для всех годов принят одинаковым и равным m_£ = m = 2,5 тыс. руб./МВт^ч. Число часов максимума потерь мощности т_тах = 5000 ч. Коэффициенты составляющих штрафной функции приняты равными ^=10 000 тыс. руб./кВ² и с₂ = 5000 тыс. руб./кВ².

Результаты оптимизации размещения БСК в тестовой системе IEEE14

По результатам оптимизационного расчета по размещению СКРМ в сети 33 кВ схемы IEEE14 предложена установка трех БСК, параметры которых приводятся в табл. 3.

В результате оптимизации уровень потерь в сети 33 кВ в режиме максимального потребления снизился с 1,070 до 0,707 МВт. Такое снижение потерь обеспечивает на горизонте 5 лет дисконтированный экономический эффект в 20 420 тыс. руб., что покрывает дисконтированные затраты на уста-

Таблица 2

Модели БСК для сети 33 кВ

X i	Тип устройства	Поле № 1 (q0)	Поле № 2 (а0)	М(хД тыс. руб.
1	0	0	0	0
2	БСК (рег.)	0,5	5	1640
3	БСК (рег.)	0,5	10	3170
4	БСК (рег.)	1	10	6220
5	БСК (рег.)	1	12	7440
6	БСК (рег.)	1,25	12	9270
7	БСК (рег.)	1,7	10	10 500
8	БСК (рег.)	2,5	12	18 420

Параметры БСК для расчетного интервала Т = 5 лет

Таблица 3

Номер узла	Число отпаек	9 ном , Мвар	Капиталовложения К(х), тыс. руб.	Издержки /(х), тыс. руб.
9	10	15	7 860	1 410
10	10	5	2 620	550
14	10	5	2 620	550
	∑	25	13 100	2 510

новку оборудования. На рис. 1 пре дс тав л ена тр а ектори я из м ен ен и я Ц Ф в х о д е ра с че та .

К роме уров ня по те рь с л ед у е т обра ти ть в н имание на выполнение ограниче ни й по доп у с т им ым уров ня м н ап ряж е н и й в с е т и. На и бол е е нагляд но с уще с т ву ющ у ю в ис х о дно й м оде л и проб л е му с на пря ж ен и ям и де мон ст рир уе т ре ж и м ра боты с е ти при от кл ючени и тра нс форм атора 5 –6 132/33 кВ, представленный на рис. 2 в виде од нолиней ной схемы с результа та м и ра с ч е та У Р из м оде л и ПК DIgSILENT PowerFactory . В та кой с х е м но р е ж и мн ой с и т у а ц ии отк л он е ни я на пря ж е н ия в узлах 12 и 13 сети 33 кВ достигают 15 % от номинала.

На рис. 3 приведена аналогичная однолинейная схема в том же режиме, но после уста- новки предлагаемых средств компенсации. Очевидно, что после ввода новых устройств, выбранных в ходе исследуемой расчетной процедуры, режим сети нормализуется – напряжения находятся в требуемом по условию расчета диапазоне ±7,5 %.

Таким образом, выбранное с применением оптимизационной методики компенсирующее оборудование, с одной стороны, позволило снизить потери в тестовой сети IEEE14, создав тем самым экономический эффект достаточный для обеспечения срока окупаемости проекта менее чем за 2,5 года, и с другой – исключило выход величин напряжений в контролируемых узлах сети 33 кВ за пределы допустимого диапазона.

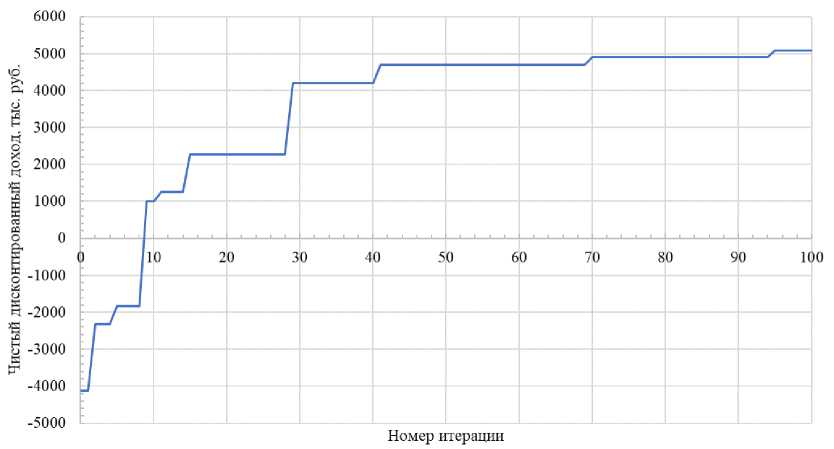
Рис. 1. Траектория изменения целевой функции в ходе работы алгоритма

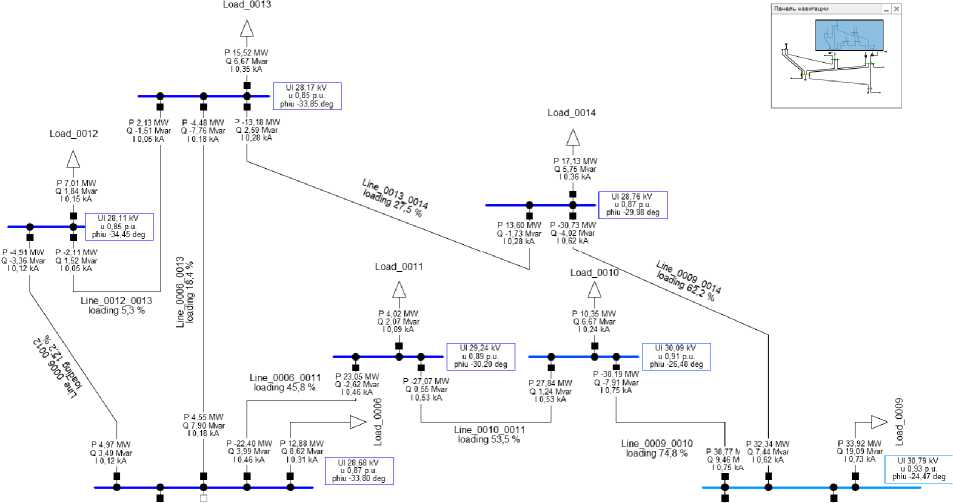
Рис. 2. Режим сети при отключении трансформатора 5–6 132/33 кВ до размещения БСК

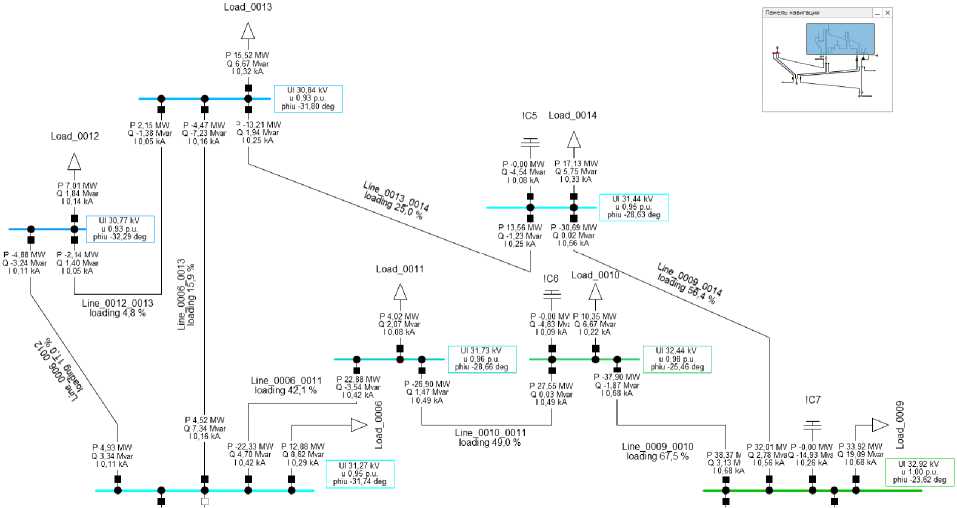
Рис. 3. Режим сети при отключении трансформатора 5–6 132/33 кВ после установки БСК

Заключение

В статье предложена, разобрана и апробирована методика применения метаэвристическо-го метода ДЭ для оптимального размещения СКРМ в распределительных сетях по критерию максимального чистого дисконтированного дохода с учетом экономического эффекта от изменения потерь мощности в сети и ограничений на допустимые диапазоны напряжений в узлах для нормальной и ремонтной схем. Результаты применения данного подхода в тестовой сети IEEE14 подтверждают его эффективность: в ходе расчетного эксперимента предложен вариант развития сети с минимальным сроком окупаемости и выполнением предъявленных к режимам требований. При этом интеграция с ПК DIgSILENT PowerFactory позволила принять во внимание существующие возможности регулирования параметров режима на стадии его расчета без дополнительных трудозатрат по его оптимизации.

Работа выполнялась при поддержке «РТСофт» – ведущей инжиниринговой компании на рынке промышленной автоматизации и эксклюзивного дистрибьютера ПК PowerFactory в России.