Оптимальное управление безопасностью промышленных объектов

Обеспечение безопасности человека, объектов и окружающей среды представляет собой многокритериальную проблему, требующую для своего решения учета многочисленных факторов, обстоятельств, условий и параметров, часто конкурирующих и противоречивых, имеющих разную масштабность, разную значимость, по-разному проявляющихся и действующих во времени. В этой сфере человеческой деятельности существуют определенные законы, управляющие взаимодействием человека и окружающей среды, которые, к сожалению, до настоящего времени остаются малоизученными [1].

В числе основных причин роста числа аварий и техногенных катастроф - высокий уровень износа основных фондов и исчерпание проектных ресурсов машин и оборудования, низкий уровень инвестиций и недостаточная нормативно-правовая база в области природно-техногенной безопасности [2]. Особенностью развития техногенной среды за последнее время является также принципиальное изменение ее системных свойств [2; 3]: возникновение рисков, обусловленных длинными причинно-следственными связями, междисциплинарный характер рисков, глобальные изменения техногенного характера, высокая чувствительность к «слабым воздействиям», сокращение возможностей прогнозирования развития аварий и катастроф традиционными методами и др.

В настоящее время разрыв между потенциальной опасностью техносферы и возможностью противостоять техногенным угрозам существенно возрос и поэтому система знаний о закономерностях в состояниях защищенности человека и окружающей среды от опасностей, сопутствующих развитию цивилизации, фактически стала самостоятельной научной дисциплиной. Наметился переход от анализа опасностей к анализу рисков, от изучения явлений, не зависящих от человека, (природных катастроф) к анализу техногенных, экологических и социальных катастроф, непосредственно связанных с деятельностью человека и являющихся следствием принимаемых решений. Это с неизбежностью приводит к необходимости использования системного подхода при проектировании и эксплуатации потенциально опасных технических объектов, анализу техногенных рисков и промышленной безопасности с использованием методов системного анализа, теории надежности, исследования операций, теории принятия решений, многокритериальной оптимизации [4-6].

Новые методы анализа и проектирования, исходя из определяющих требований безопасности и рисков, потребуют развития дополнительных разделов в традици онных теориях. При этом в анализ безопасности и рисков войдут нормы проектирования и расчетов с учетом аварийных и катастрофических ситуаций (проектных, зап-роектных и гипотетических) [1].

Научные исследования и некоторые организационноправовые решения последнего времени подготовили условия для создания системы управления риском возникновения аварийных ситуаций, перехода к оптимизации и нормированию допустимых рисков [5; 6].

Во многих практически значимых случаях оптимальность параметров системы технического обслуживания объекта может быть оценена решением одной из двух задач:

• -    обеспечением требуемого уровня безопасности (т. е. значения какого-либо показателя надежности, например вероятности отказа) при минимальных потерях и затратах на техническое обслуживание (прямая задача оптимизации);

• -    обеспечение максимального из возможных уровня безопасности при ограниченных потерях и затратах (обратная задача оптимизации).

Для наиболее сложных и дорогостоящих технических объектов, отказ которых может привести к серьезным последствиям, показатели надежности и безопасности, как более важные характеристики, обычно рассматриваются в качестве ограничения, а затраты - как целевая функция оптимизации. Поэтому в большинстве случаев решается прямая задача оптимизации.

Решение задач оптимизации техногенного риска включает, как правило, построение графа состояний, составление модели функционирования и определение таких параметров системы, при которых затраты на техническое обслуживание будут минимальны.

Оптимизация техногенного риска и определение оптимальных параметров системы технического обслуживания потенциально опасных технических объектов определяется видом и сложностью самого объекта, характером и важностью выполняемых функций, числом и видом его возможных состояний, тяжестью последствий отказов, а также стратегией эксплуатации и технического обслуживания.

Например, в модели нерезервированного объекта с периодическим техническим обслуживанием возможны три состояния и переходы четырех видов (рис. 1):

• -    из работоспособного состояния (или состояния готовности к применению) 1 в состояние технического обслуживания 2 с периодичностью ^_ТО и, соответственно, с интенсивностью переходов Х ₁₂= 1Д_ТО);

• -    из состояния готовности 1 в состояние отказа 3 с интенсивностью переходов, равной интенсивности отказов % (или параметру потока отказов): % ₁₃ = % ;

• -    из состояния технического обслуживания 2 в состояние готовности 1 с интенсивностью, которая определяется продолжительностью технического обслуживания ^Т ТО^: % 21 ~ ¹ ^ ^Т ТО^;

• -    из состояния отказа 3 в состояние технического обслуживания 2 (переход, обусловленный обнаружением скрытого отказа при техническом обслуживании) с интенсивностью переходов % ₃₂.

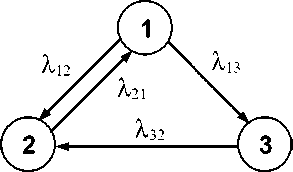
Рис. 1. Граф состояний объекта с периодическим техническим обслуживанием:

1 - работоспособное состояние (готовность к работе);

2 - техническое обслуживание; 3 - скрытый отказ (до проведения технического обслуживания)

Основным показателем надежности можно считать вероятность работоспособного состояния (состояния готовности) Р^ а при анализе безопасности основным параметром является вероятность отказа (технический риск) 5=Р₃. Периодичность / и продолжительность технического обслуживания или диагностики т _то, а также интенсивность отказов % и, соответственно, интенсивности переходов % ₁₂, % ₁₃, % ₂₁ задаются регламентом или могут быть получены по результатам экспериментальных исследований и испытаний, и при построении модели их можно считать известными. Для нахождения неизвестной интенсивности переходов % ₃₂ можно воспользоваться свойствами марковских процессов с непрерывным временем [4].

% 32 =

t TO —i

—+% t TO

1+% t TO

% t TO

Система дифференциальных уравнений для ориенти рованного графа состояний (рис. 1) имеет вид

= - ( % 12 +% 13 ) P 1 ( t ) +% 21 P 2 ( t ) = dt

• =    -f%+Л ] P 1 ( t ) + 1- P 2 ( t ) ;

^     t TO J        ^T TO

= % 12 P 1 ( t ) -% 21 P 2 ( t ) +% 32 P 3 ( t ) = dt

-

• =    Ф P 1 ( t ) - Л P ( t ) + % P ( t ) ;

t TO          ^T TO            % t TO

P^ = % 13 P ( t ) -% 32 P , ( t ) = = % P ( t )- ^ P , ( t ) .

% t _TO

Так как система (2) линейно зависима, то для решения одно из уравнений необходимо заменить нормирующим условием вида: Р^/) +Р2(/) +Р3(^) = 1. Кроме того, необхо димо задаться начальными условиями, например Р1(0)=1,Р2(0)=Р3(0) = 0.

Пусть Р₁(/) имеет изображениеР₁(х), тогда в соответствии со свойством дифференцирования оригинала -свойство преобразования Лапласа: еслафО,/(t),f'(t), ..., /"Ч /) - оригинал и его производные, и f ( t )— L — F ( x ) , то f ' ( t ) —— xF ( x ) - f ( 0 ) :

dP t

• d , ^—— xP 1 ( x ) - P 1 ( 0 ) .

  
  

Применив преобразование Лапласа и к другим вероятностям, задаваясь начальными условиями при /=0 Р1(0) =1, Р2(0) = Р3(0) = 0и учитывая, что 1 ——^1/ x , система (2) принимает вид xP (x) -1 + (%12 + %13) P1 (x) - %21 P2 (x) = 0,

- xP2 (x)-%12P1 (x) + %21 P2 (x)-%32P3 (x) = 0,

^P 1 ( x ) + P ( x ) + P ( x ) = 0.

L

Решение системы линейных алгебраических уравнений (4) имеет вид

P ( x ) =

=_____________________%32 x + x2 + %21 x + %32%21 x (%32 x + %32%12 +%32%13 + x2 +%12 x + %13 x + %21 x + %21%13 + %32%21)

P ( x ) =

% 12 x ⁺ % 32 % 12 ⁺% 32 % 13

x ( % ₃₂ x + % ₃₂ % ₁₂ +% ₃₂ % ₁₃ + x ² +% ₁₂ x + % ₁₃ x + % ₂₁ x + % ₂₁ % ₁₃ + % ₃₂ % ₂₁ )

, (6)

P ( x ) = x + %21

¹³ x ( % ₃₂ x + % ₃₂ % ₁₂ +% ₃₂ % ₁₃ + x ² +% ₁₂ x + % ₁₃ x + % ₂₁ x + % ₂₁ % ₁₃ +% ₃₂ % ₂₁ )

Для нахождения вероятностей Р1(/), Р2(/) и Р3(/) необходимо произвести обратное преобразование Лапласа. Однако полином в знаменателе формул (5)-(7) прих1 = 0 обращается в нуль, т. е. в точке х = 0 происходит разрыв

Р3 (t ) = £ Re 5 [Р3 (x ) exp (xt )] , k=1 xk где Re5ГP3 (x)exp(xt)1 = lim ГP3 (x)exp(xt)(x-xk)1,(12) Xk                            x ^ xk где и - количество полюсов (точек разрыва).

После преобразований по выражениям (10)-(12) с использованием пакета System solve Mathcad v13 получено аналитическое решение системы (2), которое позволяет рассчитывать вероятности состояний объекта при различных сочетаниях заданных параметров периодичности и продолжительности технического обслуживания и интенсивности отказов.

Графические зависимости вероятности состояния готовности от времени (срока эксплуатации объекта) при различных значениях продолжительности и периодичности технического обслуживания представлены на рис. 2.

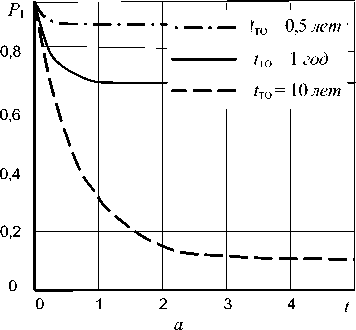
Результаты расчетов (табл. 1) показывают, что вероятность состояния готовности и, соответственно, технический риск определяются, в первую очередь, интенсивностью отказов объекта и периодичностью технического обслуживания (рис. 2, а), в незначительной степени зависят от продолжительности технического обслуживания (рис. 2, б).

Кроме того, результаты расчетов позволяют судить о продолжительности переходных процессов, в течение которой вероятность состояния готовности снижается до некоторой «финальной» вероятности, и, соответственно, о возможности использования для расчетов стационарной модели. Так, например, при X = 10^-4ч^-1 и t_T0 = 2 года после 2,5-3 лет эксплуатации значение Р₁ в дальнейшем практически не меняется (рис. 2).

Для установившегося режима эксплуатации dP₁ldt = 0, dP₂ldt = 0, dP₃ldt = 0 система дифференциальных уравнений (2) превращается в систему линейных алгебраических уравнений:

^-(X 12 + ^X_B ) ^P 1 +^X 21 ^P 2 =

= - ( t ;o +X ) p + p_o p , = 0,

X₁₂ P — X ₂₁ P 2 + X₃₂ P₃ =

_ ,         - Г / _— ,           1 - 1          , (13)

= ^t ;o ^P 1 ^{— T} ;o ^P 2 ⁺ |_ ^tto ^{— ( t}to ^{+ X)} j ^P 3 = ⁰

^X 13 ^P 1 ^{— X} 32 ^P 3 =

— 1 "I^-1

= ^{X P} 1 ^-[ ^t ;o ^- ( ^t ;o ^{+ X} ) ] ^P 3 = 0.

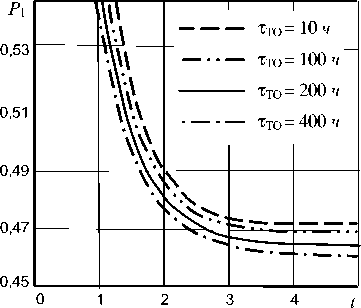
б

Рис. 2. Зависимость вероятности состояния готовности объекта от срока эксплуатации: а - Т _т0 = 10 ч, X = 10^-4ч^-1;

б - t_T0= 2 года, X = 10^-4ч^-1

При дополнении системы (13) нормирующим условием Р1 + Р2 + Р3 = 1 решение для финальных вероятностей состояний имеет вид

P 1 ⁼

P 2 ⁼

^t ;o ^{( 1 + t} ;o ^X)

22                       23          2

^v t ;o T ;o + * ;o + 2X t ;o T ;o + ^* t ;o + t ;o + ^*t ;o

T ;o ( 2X t ;o + X ² t ^ + 1 )

,(14)

^{X t} ;o ^T ;o

p =______

³ 1Д² T

^{X t} ;o ^T ;o

. ;o + 2X t ;o T ;o + X, t ;o + t ;o + X, t ;o

^{X t} ;o

* ;o + 2X t ;o T ;o + X t ;o + t ;o + X t ;o

,(15)

Некоторые результаты расчетов по формулам (14)-(16) приведены в табл. 1 (финальные вероятности Р₁) и в виде графиков зависимости вероятности состояния готовности объекта Р₁ от периодичности технического обслуживания t_T0 при различных значениях интенсивности отказов X и длительности технического обслуживания T _T0

Таблица 1

Вероятность состояния готовности объекта ( т _то = 10 ч)

t то , лет	X , ч - 1	Срок эксплуатации t, лет						Финальная вероятность
		0,1	0,5	1	2	5	10
0,5	10 - 4	0,935 8	0,882 6	0,879 8	0,879 7	0,879 7	0,879 7	0,879 7
	10 - 5	0,995 8	0,995 8	0,995 8	0,995 8	0,995 8	0,995 8	0,995 8
	10 - 6	0,997 7	0,997 7	0,997 7	0,997 7	0,997 7	0,997 7	0,997 7
1	10 - 4	0,923 2	0,772 8	0,722 8	0,709 3	0,708 6	0,708 6	0,708 6
	10 - 5	0,993 8	0,991 8	0,991 8	0,991 8	0,991 8	0,991 8	0,991 8
	10 - 6	0,998 8	0,998 8	0,998 8	0,998 8	0,998 8	0,998 8	0,998 8
2	10 - 4	0,918 7	0,702 0	0,572 4	0,491 4	0,473 4	0,472 4	0,472 4
	10 - 5	0,992 0	0,978 5	0,974 7	0,973 9	0,973 9	0,973 9	0,973 9
	10 - 6	0,999 1	0,999 1	0,999 1	0,999 1	0,999 1	0,999 1	0,999 1

(рис. 3). Обращает на себя внимание наличие экстремума (максимума), т. е. при заданных значениях % и т _то существует оптимальная периодичность технического обслуживания и, соответственно, предельное максимальное значение вероятности состояния готовности объекта [8].

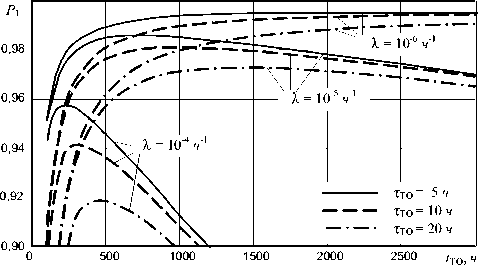
Рис. 3. Зависимость вероятности состояния готовности от периодичности технического обслуживания

Полученные аналитические решения для неустано-вившегося и решения (14)-(16) для установившегося режимов эксплуатации дают возможность решать задачи оптимизации техногенного риска.

Наряду с критерием предельно допустимой вероятности отказа для определения продолжительности работы изделия между очередными техническими обслужи-ваниями используются также экономико-математические критерии. При этом требования надежности выполняют роль ограничений.

На современном этапе развития промышленного производства безопасность техносферы трактуется как степень защищенности человека (материальных объектов) от опасностей, исходящих от функционирования технических систем. Для определения уровня безопасности используется интегрированный риск непосредственного воздействия опасности, отражающий конечный предполагаемый эффект в виде ожидаемого ущерба.

Все большее распространение получает подход к определению риска неблагоприятного события, который учитывает не только вероятность этого события (технический риск), но и все его возможные последствия. При этом вероятность события выступает одним из компонентов риска, а мера последствий (ущерб) - другим. Такое «двумерное» определение техногенного риска используется при его количественном оценивании: риск может быть определен как произведение вероятности рассматриваемого события на величину ожидаемых негативных последствий (ущерба).

Тогда задача управления техногенным риском на конкретном техническом объекте при проектировании и эксплуатации может быть формализована как минимизация функции, представляющей собой сумму рисков всех возможных событий в жизни технического объекта:

nn

⁵ = 1 R i = 1 PU , (17) i = 1 i = 1

гдер. - вероятность i-го события, U . - убытки (потери) при реализации i-го события.

Соответственно, задача минимизации функции должна решаться для всего жизненного цикла объекта с уче том наложенных ограничений как на величину вероятности отдельных событийр., так и возможных убытков Ц.

Таким образом, разработка алгоритма управления риском на основе количественно-стоимостной оценки ущерба является актуальной в настоящее время и в долговременной перспективе.

Роль экономических показателей в вопросах анализа надежности технических систем делает весьма актуальным вопрос их достоверного определения как на этапах планирования, так и во время эксплуатации технической системы. Ущерб от отказов является важнейшим экономическим показателем надежности и служит связующим и дополняющим звеном, позволяющим учесть сопряженные затраты, зависящие от уровня надежности, при расчете экономической эффективности капитальных вложений и новой техники.

Для установившегося режима и финальных вероятностей состояний оптимальная периодичность технического обслуживания, обеспечивающая минимальное значение величины техногенного риска, определяется, в первую очередь, отношением ущерба от аварийного отказа

U и затрат на техническое обслуживание С (или их отно-

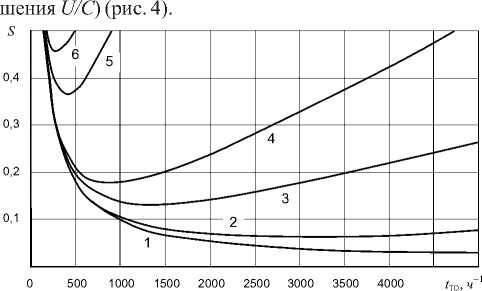
Рис. 4. Зависимость техногенного риска от периодичности технического обслуживания и отношения затрат U/С ( % = 10^-7ч^-1, Т _ТО = 100 ч): 1 - U/С = 10; 2 - 100; 3 - 500;

4- 1 000; 5-5000; 6- 10 000

Результаты расчетов оптимальной периодичности технического обслуживания Т⁷ , обеспечивающие минимальное значение величины техногенного риска 5_min при заданных параметрах интенсивности отказов % , продолжительности технического обслуживания ф и отношения убытков (потерь) при аварийном отказе к затратам на техническое обслуживание U/С представлены в табл. 2.

Например, при заданных % = 10^-7 ч^-1 и т = 100 ч, отношении затрат U/С = 100 с учетом финальных вероятностей состояний величина минимального техногенного риска S_min = 0,061 3 и оптимальная периодичность технического обслуживания T_pt= 3 066 ч = 5 мес.

Полученные аналитические решения для различных режимов эксплуатации позволяют повышать степень готовности системы, решать задачи оптимизации надежности и техногенного риска.

Приведенная методика и результаты расчетов оптимальной периодичности технического обслуживания с использованием экономико-математических критериев позволяют минимизировать техногенный риск и обеспечить оптимальное управление безопасностью потенци- ально опасных промышленных объектов, дают исходные данные для продления остаточного ресурса систем и для сокращения затрат на техническое обслуживание.