Оптимальное управление ценой при продаже скоропортящегося товара

Перед любой фирмой, производящей какой-либо товар, всегда встает проблема его сбыта. Эта проблема особенно важна для фирм, производящих товары, не подлежащие длительному хранению, так как перепроизводство товара может привести к потери им товарных качеств в течение торговой сессии, и товар будет снят с реализации или уценен. Недостаточное производство товара приведет к тому, что часть возможной прибыли будет недополучена, т. е. к упущенной выгоде.

Эти проблемы возникают при поставке товара в торговые точки, принадлежащие фирме-производителю, а также у розничных торговцев, покупающих у оптового поставщика партию скоропортящегося товара для его реализации. Во всех этих ситуациях очень большое значение имеют ответы на следующие вопросы:

• -    какой должен быть объем партии, поставляемой или покупаемой для реализации?;

• -    по какой розничной цене должен продаваться этот товар?;

• -    как должна меняться розничная цена в зависимости от остатка непроданного товара?;

• -    как управлять ценой продажи продукции, чтобы к кон

цу торговой сессии она была полностью реализована?;

• -    все эти задачи надо решать при вполне естественном критерии оптимальности - максимизации прибыли, получаемой от реализации продукции.

Постановка проблемы. Пусть имеется некоторая скоропортящаяся продукция (например, молоко, сметана, свежая рыба, овощи и т. д.), которая должна быть продана в течение торговой сессии (например, дня). В противном случае товар снимается с реализации и пропадает.

Продавец покупает партию товара объема Q 0 по оптовой цене d и продает ее по розничной цене с. Ставится задача нахождения значений Q 0 и с, при которых средняя прибыль продавца будет максимальной.

Достаточно неприятно, если к концу торговой сессии остается непроданный товар. Выбрасывать его жалко, пускать на переработку в продукцию низкого качества тоже. Поэтому продавцы применяют разнообразные приемы, чтобы реализовать товар до конца торговой сессии, например, в ее конце устраивают распродажу остатков товара по низкой цене. Однако, это не единственная и, по-видимому, не самая лучшая стратегия. Здесь имеется обширное поле для теоретического исследования. В дан- ной работе мы изучим только одну из таких стратегий управления ценой продажи товара.

Будем считать, что торговая сессия начинается в момент времени 0 и кончается в момент времени Т, т. е. она занимает интервал времени [0, T ] . Обозначим через Q ( t ) , количество товара в момент времени t. Будем также считать, что Q (0) = Q ₀ фиксировано. Будем предполагать, что поток покупателей является пуассоновским потоком интенсивности X ( c ( ' )), зависящей от розничной цены c(t).

Будем считать, что покупатели покупают товар независимо друг от друга, и объем покупки х есть случайная величина с M © = а 1 и M { ^ ²} = a ₂ .

В одном очень частном случае эта задача уже исследовалась в работе Е. В. Новицкой [1], где закон управления ценой c(t) продажи товара брался из соотношения аЛ(c(t)) = Qt) . (1)

T — t

Основные вероятностные характеристики процесса 2 ( ( ) в случае произвольной функции ц( ( / 7 ). Исследован общий случай, когда управление розничной ценой опре

Рассмотрим процесс Q ² ( t ) . Используя формулу Ито [2], легко получить уравнение, описывающее этот процесс:

d ( Q 2 ( t )) =f—-² Q 2^ ^t i+ ^a 2 - ^( t b) I    T Ф ( t / T )    a 1   T Ф ( t / T )

dt +

+ ² Q ( ' )\г ' T O T t^ dw ( ' )• a 1 T ф ( t / T )

Обозначим M { Q ²( t )} = Q ₂( t ) . Тогда, усредняя уравнение (7), получим

dQ. ( ' ) = |— 2^ + ^

²      ( T Ф ( t / T ) a 1 T Ф ( t / T )

или, с учетом выражения (6)

dQ 2 ( ' ) =_— 2 Q 2 ( ' ) ₊

dt

T ф ( t / T )

деляется соотношением

V         Q ( ' )

a;"(" Wrn ■

Найдем характеристики величины количества товара в диффузионном приближении. Процесс Q ( t ) может быть приближенно описан следующим стохастическим дифференциальным уравнением [1]:

dQ ( t ) = — a 1 X ( c ) dt + J a ₂ X ( c ) dw ( t ) , (3)

где w ( t ) - стандартный винеровский процесс. Именно эту аппроксимацию мы и исследуем ниже.

Объединяя выражения (2) и (3), можно сказать, что диффузионная аппроксимация процесса g(t) имеет вид

dQ ( t ) = —

Q ( ' ) T ф ( 11T )

dt +

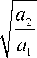
Q ( ' ) —

T ф ( t / T )

dw ( t )

Найдем основные вероятностные характеристики процесса Q ( t ) .

Обозначим M { Q ( ' )} = Q ( t ) . Для краткости записи, аргумент t у Q(t) и Q ( t ) мы часто будем опускать.

Усредняя уравнение (4) с учетом того, что приращения винеровского случайного процесса независимы и

имеют нулевое математическое ожидание, получим следующее уравнение для Q ( t ) :

dQ ( ' ) = —

Q ( ' ) T Ф ( t / T )

dt

которое является дифференциальным уравнением пер

вого порядка с разделяющимися переменными и которое надо решить при начальном условии Q (0) = Q ₀ . Его решение имеет вид

Q ( t ) = Q _o exp - — ---—--- • =

⁰      [ ^J ₀ T ф ( x / T )

Г 'T , „ i

= Q0exP 1 — J — ■•

0 Ф ( z )

В частности,

—               r dz

Q ( T ) = Q 0 exp j— J- d U .

0 Ф ( z )

dt

+

г dx ^a 2 ^Q 0 ^exp I—, _IT.

0 ^T Ф ⁽ X / ^T )

a 1 T ф ( t / T )

,

которое надо решить при начальном условии Q ₂ (0) = Q ₀ ² . Решая это уравнение, получим

t / T

' ' ^f

Q 2 ( t ) = Q 02 exp j— 2 J - 0 Ф ( z )

a ₂

а 1

t / T

r dz

^{Q ex}P M   ,

> Ф( z )

t / T

+

x

' f dz x 1 — exp — ---- ^ •

^J 0 Ф ( z )

Отсюда

D{Q ( ' )} = D q ( ' ) = Q 2 ( ' ) — Q ²( ' ) =

a2              dz

= — Qexp ^ I — ai             о Ф(z)

1 — exp - — [ - dz- ■ . (10) ^J 0 Ф ( z )

Математическое ожидание выручки и его оптимизация. Рассмотрим случай, когда зависимость X (c) может быть аппроксимирована прямой линией

X ( c ) = X 0 —X 1 c-c ° .

c ₀

Здесь с₀ имеет смысл некоторой «стандартной» цены, так что X ( c ₀) = c ₀ . Такая аппроксимация возможна, если отклонения цены с от с₀ незначительны.

В этом случае уравнение (2) приобретает вид

Г.              c ^

a 1 X ( c ) = a 1 1 X ₀ + X 1 — X 1 —

I                    c 0

Q t ф ( t / t ) ^,

откуда

^c = ^c 0

1 + ^

—

Q )

X 1 a₁ X ₁T ф ( t / T )

.

Так как в единицу времени в среднем совершается X (c) покупок, средний размер которых равен а₁ по цене с, то среднее значение выручки в единицу времени равно

LX, ca i X ⁽ c ) = c 0 1 ¹ + — I      X.

—

, 1 a 1 X 1 T ф ( t / T )

Q

x

T Ф ( t / T )

•

Усредняя по объему партии товара Q(t), имеющегося в наличии в момент времени t, получим

J

¹ - J Тф^ "

- c -1- , Q =

⁰ « 1 x 1 т V( t / t )

S = cQ- x

X

( X 0 + X 1 ) ( 1 - e ^{-ф (1)} ) -

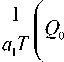
« 2 Г « 1 J^J 0

e -^{2v( z} V²

( z ) dz

, L>0 ^{J Q}     c 0     Q 2

1 +

⁰ |   X 1 J T ф ( t / T ) « 1 X 1 T V( t / T )

Подставляя сюда явные выражения для Q и Q ₂ полу

чим, что средняя выручка в единицу времени равна

M {c«₁ X ( c )} = c ₀

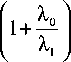
Q о _х

T ф ( t / T )

dx

T ф ( x / T )

х exp - J

^c 0 ^Q 0 _____

« 1 x 1 т V( t / t )

exp - 2 J

dx

T ф ( x / T )

« 2         f

~ eXP I

« 1        Г.

dx

T ф ( x / T )

х

Отсюда средняя выручка за весь период торговой сес

сии равна

z

-      J e -*^{( z} V²( z ) dz

« 1^T t

Таким образом, S представляет собой функционал от функции ф ( z ) , который с точностью до постоянного

слагаемого и сомножителя равен

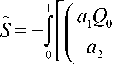
- 1 e ^{-2ф ( z} )

+ e ^{-ф ( z} )

x

S = J M { c« 1 X ( c )} dt .

Подставляя выражение (15) в уравнение (16) получаем

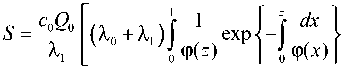
dz

z dz

,г dx ^exP1 ²J

О ф^{( x} )

-

хф' ² ( z ) dz , и нам надо решить задачу S => max с граничным условием ф (0) = 0 .                     ^{ф (} ' )

Мы имеем дело со стандартной задачей вариационного исчисления. Используя уравнение Эйлера [3], можно получить, что ф ( z ) удовлетворяет следующему дифференциальному уравнению

Ae "^ф ( ф'-ф' ²) + |V- 1 ф² J= 0 ,      (21)

л «1 ^Q 0 1

где A =-- 1 .

« ₂

Рассмотрим сначала приближенное решение этого уравнения. В реальных ситуациях объем партии товара достаточно велик, и поэтомуИ»1. Поэтому в уравнении (21) главную роль играет первое слагаемое. Пренебрегая

-

1 ' ф ²( z ) «T ^J Г

х

«2       Г dx 1 n exP -1 + Q0 «1         00 ф(x)

.

Для упрощения дальнейших вычислений введем вспо

могательную функцию ф ( z ) вида

z

ф( z ) = j- dx- ,                (18)

00 ф ^{( x} )

тогда ф' ( z ) = —- , а ф (0) = 0 ■ ф ( z )

Теперь выражение для S принимает вид S = cQ х

X

Г ¹

(X +Х1 )J х^ 0

e ^{-ф (} z V( z ) dz - -1; I Q 0 «T I

« ₂

X

J

1                                л 1

x J e ^{- 2 ф ( z} V² ( z ) dz --J e ^{-ф ( z} ) ф' ² ( z ) dz

0                           « 1 ^T 0

Первый интеграл легко вычисляется

J e-ф(z Y( z) dz = 1 - e-ф(1), так что окончательно

вторым слагаемым, получим уравнение ф"-ф/2 = 0,(22)

которое надо решить при граничном условии ф (0) = 0 .

Решение этого уравнения имеет вид

ф(z) = lnC1 - ln(C1 - z).(23)

Отсюда

ф(z) = C1 - z ,(24)

что и дает окончательный вид функции)(г).

Очевидно, что должно быть C 1 >  1 , иначе торговля нашим товаром закончится в момент времени C 1 T <  T , что совершенно не нужно. При С₁ = 1 торговля закончится не позже момента времени Т, а при С₁ > 1к моменту времени Т часть товара может остаться непроданной.

Рассмотрим теперь задачу о выборе оптимальных значений параметра С₁ и величины партии товара, выставляемого на продажу Q₀. Сначала рассмотрим задачу о выборе оптимального значения С₁при фиксированном Q₀. В дальнейшем будет использовано обозначение 1, C 1 = С.

Подставляя наше решение в выражение для S, полу

чим

х

S = cQ х x 1

( Х 0 +Х 1 ) С - A- 1 Q 0 - « 2 ^J С ² + «^ С ln(1 - С ) « 1 T |       « 1 J       « 1 T

Приравнивая нулю производную от 5 по С, получим уравнение

Э5 „, ~

— = / 1 ( C ) = 1 0 + 1 1

c ₀

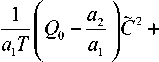
a 2 C ²

а 1 ² T 1 - С

■ d - c ^Q 1 1 а 1 T

-

^^^^^^.

= 0.

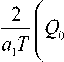
a ₂

С + a ₁ 2 T

С

С С 1n(1 - C ) - 1 C С

= 0.

Заметим, что 0 <  C <  1 ■ Далее, / 1 (0) = 1 ₀ + 1 1 >  0 и с 1тт 0 f_x ( C ) = -~ ■ Вычисляя производную от / (С ? ) по С, получим

При раскрытии скобок слагаемые, содержащие Q ₀ , сокращаются, и мы получаем уравнение относительно С:

- c ^а 2 С ² + ^са 2 ^C - d = 0 ,

1 1 а 1 ² T      1 1 а 1 ² T 1 - C

или, в более простом виде,

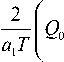
a ₂

a ₁

\

C ³ da 1 ²

С          1 1 T

1 - C с 0 а 2

(З1)

а ( 1        1

а 1 ² T I 1 - C (1 - C )²

< 0.

Это уравнение сводится к кубическому уравнению и

С               С

Таким образом, при изменении С от Одо 1, / (С)

монотонно убывает от 1 ₀ +1 1 >  0 до - ^ . Это говорит о том, что уравнение (26) имеет единственный корень, ле

жащий в промежутке от Одо 1. Его можно найти только

легко решается численно.

d a ₁

Легко получить, что с ростом выражения--1T c0a2

значения С быстро приближаются к 1. Так как 1^ обычно велико, то эта ситуация и имеет место на практике.

В этом случае приближенно уравнение (З1) можно

численно.

При этом следует иметь в виду, что обычно 1 ₁ очень велико, так что на самом деле С и С₁ близки к 1 .

Оптимизация по объему партии товара. Существует также оптимальный объем партии товара Q_№ выставляемый на продажу Так как себестоимость единицы продукции равна d, то прибыль, получаемая от продажи партии товара объема Q_o с учетом выражения (25) равна

заменить уравнением

= ^ ^а 2 1 1 T ,

1 - C с 0 а 2

откуда получаем приближения для С и C 1 :

с= 1 — ^с.^а 2 , C = 1 + -О^-da ₁ ² 1 ₁ T     ¹       da ₁ ² 1 ₁ T

.

(З2)

c 0 Q 0

T

P = J M { са 1 1 ( с )} dt - dQ ₀ =

С 1 ( _ ^{( 1} 0 ⁺¹ 1 ) ^C --у I Q 0 ^a 1 T I

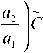
-4 C 1n(1 - С ) a ₁ 2 T

^{- dQ} 0 .

Оптимальный объем партии Q _o определяется из условия d PJ д Q ₀ = 0 , что приводит к уравнению

c ₀

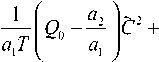
Зная С из уравнения (29) легко находится и оптимальный объем партии товара Q ₀ :

a 2             a 1 T

Qo = —+ (1(> +1])--+ a1            2C

+ J2U_

2 a 1 C

с

1П(1 - C ) - 1 C С

(ЗЗ)

Для выяснения того, когда можно пользоваться этим приближением, рассмотрим вопрос о точном решении уравнения (21). Можно показать, что его решение может быть записано в следующем виде:

a ₂ 2 a ₁ ² T

~     ~

C 1n(1 - C )

- d

-

c ^Q С ² = 0 a₁ 1 ₁T

z =      ^

4 A ( A + 1)

Теперь нужно решить систему двух уравнений (26) и

(29). Упростим ее.

С

Умножая уравнение (26) на С приведем его к виду

С 1 ( „ ^{( 1} 0 ⁺¹ 1 ) ^{C -} I Q 0 aT I

^а 2 С ² +

^а 1 7

си -       ~

+ -Ъ С 1n(1 - С ) = a ₁ 2 T

(ЗО)

С 2

П ^а 2 ^С 2 , ^а 2 ^C

QQ C +           .

⁰ а а 2 T 1 - С

¹ 7             ¹

В квадратных скобках уравнения (29) стоит та самая комбинация, что и в первой строке соотношения (ЗО). Заменяя ее той комбинацией, которая стоит во второй строке уравнения (ЗО), получим

4 A ( A + 1) -

- 4 Aw ( Aw + 1) +

+ 21n(2 A + 1 + 2 4 A ( A + 1)) -

- 21n(2 Aw + 1 + 2 4 Aw ( Aw + 1))

ф = C1

( Aw + 1) w A + 1

(З4)

которая в параметрической форме дает зависимость между z и ф . При этом параметр w меняется в пределах 0 <  w <  1 .

Заметим, что при A ^ ^ эта система переходит в

z = C 1 - C 1 w , Ф= C 1 w ,

откуда получается, что ф ( z ) = C 1 - z , т. е. та же самая зависимость, что и в приближенном решении.

Для выяснения вопроса о том, при каких значениях параметра^ приближенное решение достаточно точно,

приведем графики зависимости ф от z при различных значениях параметра Л (см. рисунок).

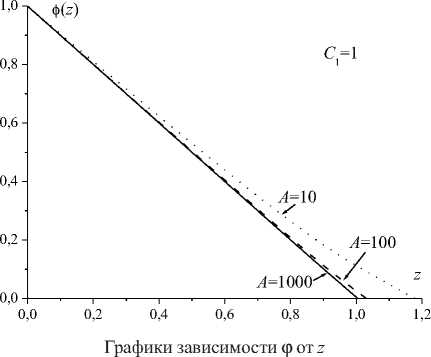
Уже при Л =100 различие между точным и приближенным решениями невелико, а приЛ = 1 000 это различие практически незаметно. Для C1 > 1 выводы анало гичны. Поэтому можно утверждать, что приближенным решением можно пользоваться при A > 100 .

Заметим еще, что в основном различие между точным и приближенным решениями проявляется при z = 1 , т. е. в конце торговой сессии, когда t близко к Т.

Таким образом, найден оптимальный закон изменения продажной цены товара в зависимости от времени и количества непроданного товара, а также оптимальный объем партии товара, выставляемого на продажу.