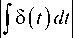Оптимальное управление процессами с рециркуляцией взаимодействующих потоков

Одной из характерных особенностей процессов ректификации является рециркуляция взаимодействующих потоков, что приводит к специфичным граничным условиям в краевых задачах. В этом случае технологический процесс описывается уравнениями в частных производных, а граничные условия – дифференциальными уравнениями с обыкновенными производными [1]. С учетом этих особенностей авторами сформулирована и решена задача оптимального

y‘ = 7 [( w—l—f )Z(2)+ к (У * (x)—У)]- y , yl =Z(2), 0 < t < T,  0 < l < 1,

при краевых условиях:

xt = 1T [(L + F) x + (W — L — F) У — Wxk >Xk, H

управления.

Математическая модель управляемого процесса представлена следующими дифференциальными уравнениями в нормальной форме:

xk

У ^- a ^[ y k* ( xk ) ^- x k ]^- x k = 0, ⁰ <  t <  T,

l = 0,

x = 7 [(L+L K™

*

+—x+K (y - y (x))+Fф xx

x =^ ,

- X,

xdt = 1Г [L + F — W ]( yd - xd )  Xd ,

^H x d

(L + F — W)(yd -y) — L(xd -x) = 0, yd -У -Ed (yd (xd)-У) = 0, 0 < t < T, 1 = 1,

при начальных условиях:

x(l,0) = x0 (l), y(l,0) = y0 (l),        0 < l < 1, xd (0) = xdo, xk (0) = xko, 0 ^ a, Ed ^ 1.

и ограничениях на управления:

^{( L} - ^L min ) ^{( L} max - ^L ) - u ² = ⁰,

( W - W min )( W max - W ) — Z 2 = 0.

Пусть L , W – оптимальные управления; u , z – соответствующие им (согласно (5)) вспомогательные

управления; x ,

y , x_k , x_d , y_d – оптимальное реше-

Здесь u , z – вспомогательные управления; x , y – концентрации целевого продукта в жидкой и паровой фазах, мольные доли; x_f – концентрация целевого продукта в разделяемом сырье, мольные доли; F – поток сырья, кмоль/ч; L , V – потоки жидкости и пара в аппарате, кмоль/ч; Ф x ( l ) - функция распределения потока по длине объекта; H_x , H_y – удерживающие способности аппарата, кмоль/м; H_x , H_x – удерживающие способности в кубе и дефлегматоре, кмоль/м; W – отбор продукта внизу объекта, кмоль/ч; D – отбор целевого продукта вверху объекта, кмоль/ч.

Сформулируем следующую задачу оптимального управления: во множестве кусочно-непрерывных функций L , W , удовлетворяющих условиям (5), найти такие, что соответствующее им решение задачи (1)…(4) дает минимум функционалу

F = JJ (y (l, t)-0* (l, t))2 dldt, где 0* (l, t) - заданное значение концентрации целевого продукта.

Для получения необходимых условий оптимальности в форме Лагранжа–Эйлера рассмотрим вспомогательный функционал [1; 2]:

I = I, +12 = JJ L dldt + J ldt, n         an где

L = ( y -0 * ) 2 + e^{( 1 )} ( x t - X ) + e^{( 2 )} ( x l - ZС» ) +

+ n^{( 1 )} ( y t — Y ) + n^{( 2 )} ( y l -Z^{( 2 )} ) ,

~ = Xk1)( xkt - Xk ) + 42)( y - xk - a (yk (xk)-xk)) ++ Xd1)(xdt-xd) + Xd2)((L+F- W)(yd -y)-L(xd -x)) +

⁺ ^ d ^3>( y d ^{- y -} E d ( y d ⁽ x d ^{)- y} ) ) ^{+ Y} ( ^{( L - L} min ^{)( L} max - ^{L )-} u 2 ) ⁺ + s ( ( W - W mn )( W max - W ) - 2 ² ) ,

ние задачи (1)…(4), соответствующее этим уравнениям; 5 L , 5 W - вариации управлений L , W ; 5 u , 5 z -соответствующие вариации фиктивных управлений u , z ; 5 x , 5 y , 5 x k , 5 x d , 5 y d - соответствующие вариации решений. Тогда, используя аргументацию вариационного исчисления, получим сопряженную задачу относительно функций Лагранжа e , П , X k ) ,

Xw

^X d ,

–

n‘

Y , s:

при 0 <  t <  T , 0 <  l <  1

L + L* ^e t - ^r x

L + F - W

-

H y

- при l = 0,

l-n.

dX^

dt

– при

– при

^e‘ = k y ⁽/)U

n ‘ =^{- k} y

0 < t < T

—

X k ¹

e

H x

)

V

—

-

l x

n

H y 7

,

e

H x

-

Hni+2 (y-0*);

у 7

x ( 1 )

= 0, H x_k

Hk-_V^{L +} F - ^W_H- ..=°,

x k 7

= Hr- xk^i)+X k ²⁾|^- a ( y k ) + a - 17, x_k

t = T , 0 <  l <  1

e= 0, n= 0,

l = 1, 0 < t < T

^ H ^ + X d ²⁾7 L -X d E d ( y d ) ‘= 0,

_n + ^X < 2) ( L + F - W ) + ( 1 - E d ) ^X < 3) H

l y 7

d Xd _ L + F - W

dt

H x d

= 0,

X d ^-X d²’ L ,   X < ¹⁾( T ) = 0,

f x^{(1 )}

Ht

l xd

-

Xd ( L + F - W ) -X < ³⁾= 0;

здесь e^{( 1 )} , e⁽ 2 ) , n⁽ 1 ) , n⁽ 2 ) — функции, определенные на П ( П = { ( l , t ) |0 <  l <  1,0 <  t <  T } ) ; X k ⁰, X d ) , y , s - функции, определенные на [ 0, T ] (их можно считать определенными на 9Q ), причем s = X k ) = 0 на 5Q /{ ( l , t ) | l = 0}, Y = X d = 0 на 5Q /{ ( l , t )| l = 1}.

- при 0 < t < T

1 f J ' ⁰ 1

- A x +2L y

Hl Hl

x

y

X^{( 1 )}                                      X^{( 1 )}

dl - 7T" (x (0, t)-у (0, t))+7T"+ HH

xk

H

xd

+ (yd + xd ) + Xd2)(y (1,t)-yd + xd -x

-Y ( L min + L max - 2 L ) = 0,

-

1     _n               x^{( 1 )}                   x^{( 1 )}

J —Ъ^- y ‘ ^{dl —} TT^{- (} y d ^— x d ^{) +} "77~ ( xk ^— y ⁽0, t ) ) -

0 H y        H x d            H x k

- X d ²⁾ ( y ( 1, t ) - y d ) + s ( W . + W max - 2 W ) = 0, у u = 0, s z = 0.

Эти необходимые условия отличаются от известных условий стационарности соотношениями (10). Это отличие связано с тем, что управления L , W являются граничными управлениями, но одновременно входят и в уравнения процесса, так что их вариации в Q и на dQ не являются независимыми.

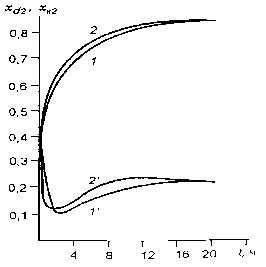
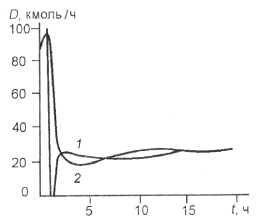
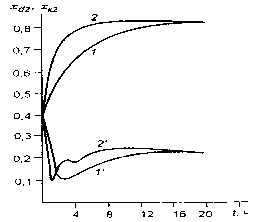
Теперь получим необходимые условия оптимальности в форме Вейерштрасса. Пусть L , W – оптимальные управления. Приращение функционала, вызванное переходом от оптимальных управлений L , W и соответствующих им решений x , y , xk системы (1)…(4) к произвольным допустимым управлени- ям L = L + AL , W = W + A W и соответствующим им решениям x + Ax, y + Ay , xk + Axk представим в виде

T

A I = J [ A A L + B A W ] dt + JJ s ₁ dldt + J s ₂ dt ,

Q         SQ где

A = 7rJⁿ yd

H y 0

^—/ J ^ ^x ‘ ^{dl +} ЧТ ^X k ( y ( ⁰, t ) ^{— x} ( ⁰, t ) ) ^—

H x 0        H x_k

^{( x ( 1}, t ^)— y ^{( 1}, t ) ) ;

H x d

B =

7г j n y d ^A- ( x k ⁽ t ^)— y ^{( 0,} t ) ) ^—-^ d - ( y ^{( 1,} t ^)— x ^{( 1,} t ) ) ; H y 0       H x_k                 H x_d

2 A L , A W , x s

S i =A y + — A x ^ ——A y n i + 0 ( A x ) ; HH

y

x

S 2 = —^ L ( A x ( 1, t ) ^ ( 1, t ) —A x ( 0, t ) ^ ( 0, t ) ) + H_x

+ ^ ( A у ( 1, t ) n ( 1, t ) — A y ( 0, t ) n ( 0, t ) ) +

Hy

■ ^Л' ( a w A x _k —A L A x ( 0, t ) + A W A y ( 0, t ) ) +

^H x k         ^k

+ ^ A W ( A y ( 1, t ) —A x ( 1, t ) ) + 0 ( A x ) .

H x d

Здесь A x , A y , A x_k определяются из уравнений

H_x A x t — ( L + A L + L ) A x ‘ =

*

= ^L- ^— k y ( y *) A x + k y A y + x'AL + 0 ( A x ) ,

H y A y t + ( V + A V ) A y ,= k y ( y ) A x — k y A y — y ,A V + 0 ( A x ) ,

0 <  l <  1, 0 <  t <  T , H x A x k = ( L + A L + F ) A x ( 0, t )

—

—

( V + A V ) A y ( 0, t ) + ( W + A W ) A x_k + + x ( 0, t ) A L — y ( 0, t ) A V + x_k A W ,

A y ( 0, t ) = ^ a ( y k ) — a + 1 jA x_k + 0 ( A x_k ) , l = 0, 0 <  t <  T ,

H x_d A x ; ( 1, t ) = ( V + A V ) ( A y ( 1, t ) — A x ( 1, t ) ) + + ( y ( 1, t ) — x ( 1, t ) ) A V , l = 1, 0 <  t <  T ,

A x ( l ,0 ) = A y ( l ,0 ) = A x_k ( 0 ) = A x ( 1,0 ) = 0 0 <  l <  1,

A V = A L — A W .

Производные A x ‘ , A y ‘ считаем ограниченными.

Для оценки приращений используем следующий результат, легко получаемый из известного неравенства Гронуолла: если

|Ф( t )| < M P 1

t^

+ J(^(T)| + V(T)) dT t0

P₁, M = const,

ф(т)> 0, tо

тогда

f)

ф(t)<^M1 P1 ⁺|v(t)dT ,

I      00

M₁= const,      1₀< t< T .

Из первого уравнения (12) получим неравенство

t

|^Axk (t)|< N। J(|^Axk (^T)| ⁺ |^Ax(⁰,^T)| ⁺ I^Ay(⁰,^T)l)^{dT +} 0

+ N2 J(|al (t )| + |a W (t )|) dt, а в силу (17) будем иметь

t

|Axk (t)|< N3 J(|Ax(0, t)| + |Ay (0, t)|)dt +

+ N4 J(|AL (t )| + |A w (t )|) dt.

Из второго уравнения (12) и (17) следует оценка

IAy (0, t )|< N5 J | Ax (0, t)| dt +

T

+ N₆J(|AL (t )| + |A W (t )|) dt.

Аналогично из (13):

t

I Ax (1, t )|< N7 J|Ay (1, t)| d t +

+ N8 J(|AL (t )| + |A W (t )|) dt.

Учитывая, что левые части (11) представляют производные вдоль характеристик (с точностью до постоянного множителя), и интегрируя вдоль этих характеристик, получим:

| Ax (l, t )|< N9 J (|Ax (l (т), т)| + |Аy (l (т), т)| + t0

+ \AL (t)| + |a W (т)|) d т + |Ах (l0,t0)1,

| Ay (l, t )|< Nio J(|Ax (l (т), т)| + |Аy (l (т), т)| + t0                                                                        ,

+ |AL (т)| + |А W (т)|) d т + |Ах (lO', t0)|, где (l0', t0), (l0", t0) - начальные точки соответствую щих характеристик, 0 < t0, t0 < t, причем t0 = 0 или l0 = 1, 100 = 0 или 100 = 0.

Пусть

а( t) =

max 0<т<t, 0< l<1

| Ax (l, т)|

^e(t)=mmax l^Ay^(l, ^т)1.

0<l<1,

Тогда из (19) и (20) имеем

|Ax(l, t)|< N9 J(а(т) + ₽(т))dт + N9 J|AL(t)|dt + 00

+ N7 J ₽(т) d т + N8 J(AL (t )| + |A W (t )|) dt, 00

откуда

a(t)< N11 J(а(т) + р(т))dт + N12J(|AL(t)| + |aW(t)|)dt.

Аналогично можно получить оценку

в(t)

Еще раз применим (18):

a(t)< N15 J₽(т)dт + N16J(|AL(t)| + |AW(t)|)dt, 00

в(t) < N17Jа(т)dт + N18J(|AL(t)| +1AW(t)|)dt.

Интегрируя от 0 до g , учитывая, что при f (т) > 0

J dt \f (т) d т =J d тJ f (т) dt =

0    00

CT

= J(g т) f (т) d т< TJ f (т) d т, и заменяя g на t, получим

Jа(т)dт< N19J₽(т)dт + N20J(AL(t)| + |AW(t)|)dt, 000

J₽(т)dт< N21Jа(т)dт + N22J(|AL(t)| + |AW(t)|)dt.

Подставляя в (21) и еще раз применяя (17), приходим к оценкам вида

а( t )< PJ(|AL (t )| + |A W (t )|) dt,

T

в( t )< p J(|al (t )| + |a w (t )|) dt, откуда

I Ax (l, t )|< pJ(|al (t )| + |a W (t )|) dt,

(22) T

IAy (l, t )|< P J(|AL (t )| + |A w (t )|) dt.

Теперь мы можем оценить s1, s₂. Обозначая 5(t) = |AL(t)| + |AW(t)|; q - наибольшее количество слагаемых в формулах для е1, е₂; 51 - максимум модулей коэффициентов при приращениях в этих формулах, получим:

Is, (l,t)| < P21 T5(t)dt | 5,q5(t)PT5(t)dt,

I^J0         J              0

|s2 (l, t)|< q515(t) PJ5(t) dt.             (23)

Сформулируем необходимые условия оптимальности в виде теоремы.

Теорема. Если L (t), W (t) - оптимальное управление, x , y , x_k – соответствующее решение задачи (1)…(4), то в точках непрерывности управлений

A AL + B A W > 0

для всех допустимых приращений AL , A W , или что то же самое,

_L (_t ) = /^Lmax при ^A ( t )< ⁰, [^Lmin при ^A ( t )>⁰,

_W (_t) = /^” при ^{B (}t)< ⁰, [^Wmin при ^B (t )>⁰.

Доказательство. Пусть t₀– точка, в которой условия (19) нарушаются, например для L (t). Возьмем s > 0 так, что при 1₀< t< 1₀+ s

A (t )< 2 A (t 0),

^L ( t )< 2 ( ^L ( t 0 ) ^{+ L} max ) в случае ^А ( t0 )< ⁰,

A (t )> 2 A (t0),

^L ( t )> 02 ( ^L ( t0 ) ^{+ L}min ) в случае A ( t0 )>⁰, и выберем приращения

0 при t e[0,1₀]U[1₀+s,T],

^L max — ^L ( t 0 ) при t 0 < t< t 0 ^+S

AL (t) = s в случае A (1₀) < 0,

Lmin — L ( t0 ) при t0 < t < t0 +S в случае A (10) > 0,

AW (t )=0.

Тогда при t0 < t < t 0 +8

A(t)NL(t) < a < 0,

для управляющих функций такие же, как в первых пяти вариантах (рис. 3).

где

a = s

, 4 A⁽t⁰⁾⁽Lmax 44 A (10 )(Lmin

- L ( t 0 )) при

-L( t0)) при

A (t0 )< 0,

A (10 )>0,

T

j[ A NL + BN W ] dt < a 8

jj 81 dtdl < b18² Q

T j 82dt < b2

Рис. 1. Графики переходных процессов по концентрации бутана в дефлегматоре и кубе в пусковом режиме:

1, 2 – в дефлегматоре; 1′, 2′ – в кубе; 1, 1′ – при начальном управлении; 2, 2' – при оптимальном управлении; управляющий параметр – отбор вверху колонны

где b, b1, b₂ - постоянные, не зависящие от 8; NI < a8 + b18²+ b₂8²при достаточно малом 8, что противоречит оптимальности управлений L (t), W (t). Аналогично рассматривается случай, когда (24) не выполняется для W (t) .

Как видим, доказательство теоремы указывает на способ улучшения управлений, если условия (24) не выполнены. Это позволяет построить итеративный процесс улучшения управлений при нарушении условий (24).

В качестве примера рассмотрим задачу оптимизации пускового режима для промышленной колонны К-34. Исходные данные: F = 103,65 кмоль/ч, F_v = 0, D = 27,06 кмоль/ч, L, = 45,21 кмоль/ч, Vd

W = 76,59 кмоль/ч, H_v = 50 кмоль, H_v = 30 кмоль, x_d                              x_k

PH = 3,6 ат, РВ = 3,5 ат. Коэффициенты P1 i, P₂i, P₃i

Рис. 2. Графики оптимальной функции управления (отбор вверху колонны):

1 – в пусковом режиме; 2 – совместно с другими оптимальными управляющими функциями L_d , F, l_f , x_f2

получены методом наименьших квадратов с использованием таблицы зависимости давления чистых компонентов от температуры. Состав сырья: x_f = 0,029 63, x_f = 0,222151, x_f = 0,143 95, f₁                                               f₂                                                  f₃

xf = 0,044 52,      xf = 0,043 89,      xf = 0,420 21, f4                                             f5                                             f6

х_Л = 0,096 3 [3].

Выберем целью управления достижение в выходных потоках концентраций компонентов x_diсти x_kiст.

В этой задаче возмущением является начальное состояние управляемого процесса, при котором концентрации компонентов по длине колонны равны концентрациям этих компонентов в сырье. Время управления Т возьмем 20 ч.

Были проведены расчеты шести вариантов задачи оптимизации пускового режима.

В первых пяти вариантах задача оптимизации решается с одной управляющей функцией. Значения остальных четырех функций и начальное значение управляющей функции заданы такими же, как и при расчете статического режима (рис. 1, 2). При начальном управлении значение функционала для всех вариантов задачи одинаково: F⁰= 34,0.

В шестом варианте задачи в качестве управляющих взяты все пять параметров. Начальные значения

Рис. 3. Графики переходных процессов по концентрации бутана в дефлегматоре и кубе в пусковом режиме: 1, 2 – в дефлегматоре; 1', 2' – в кубе; 1, 1' – при начальном управлении; 2, 2' – при оптимальном управлении; управляющие параметры: отбор вверху колонны, орошение, расход сырья, концентрация бутана в сырье, координата ввода сырья

В результате решения было получено, что наиболее эффективной управляющей функцией является L_d (поток орошения) (см. таблицу). Однако следует заметить, что увеличение потока орошения значительно увеличивает энергетические затраты.

Следующим по эффективности управляющим параметром является концентрация бутана в сырье x_f . Управление этим параметром связано со значительным перераспределением выходных потоков в предыдущей колонне, что не всегда допустимо.

Сравнительная оценка управляющих параметров при оптимизации пускового режима колонны

uj	D	FL	lL	Ld	xf2
F ■ min	28,5	29,6	30,4	20,9	26,2

Наименее эффективным управляющим параметром является координата ввода сырья l_L , однако изменение этого параметра осуществляется практически без дополнительных энергетических затрат.