Оптимальное управление процессом разделения с ограничениями на потоки

В настоящее время мощное развитие получили теория и практика систем с распределенными параметрами [1–9]. Это обусловлено, с одной стороны, наличием современных наукоемких технологий в металлургии, нефтепереработке и нефтехимии, энергетике и других отраслях промышленности, с другой – разработанным перспективным математическим методом анализа гидротермодинамических процессов и систем управления с целью проектирования высокоэффективных производств [10–24]. Произошло весьма продуктивное соединение современного математического аппарата с нуждами практических проблем в промышленности и современными вычислительными технологиями. Важным обстоятельством выступает тот факт, что основу большинства непрерывных промышленных производств составляют процессы тепломассообмена в условиях сложных гидродинамических явлений, например в условиях суперкавитации [11, 13, 23, 24]. Однако совместное рассмотрение и изучение вышеназванных процессов довольно сложная задача, и в последнее время в основном изучают с различных точек зрения теоретические и прикладные задачи раздельно, мало учитывая влияние одних процессов на другие.

Вычислительные технологии объединяют новейшие достижения математических методов с нуждами производства, несмотря на то, что они развиваются самостоятельно, но тем не менее влияют друг на друга. И только в вычислительных технологиях достигается совершенство математических абстракций и реального производства, решаются различные системы уравнений в частных производных в области постановки краевых задач, аналитических и численных методов, вопросы качественного исследования краевых задач и задач оптимального управления. Результатом этого эволюционного процесса могут являться разработанные науч-– 160 – но обоснованные методы расчета основных технологических и конструктивных параметров (геометрических, гидротермодинамических и кавитационных) при проектировании надежных и высокопроизводительных технологических аппаратов в различных отраслях промышленности, в которых происходят процессы тепломассообмена и гидродинамики взаимодействующих потоков. Важными остаются вопросы степени адекватности математического описания этих процессов реальным режимам технологических объектов. Для различных условий адекватность может быть разной. Необходимо, чтобы точность математического описания соответствовала требованиям конкретного производства.

Значимым элементом вычислительных технологий являются системы с распределенными параметрами, которые функционируют в условиях управления, в том числе оптимального. Распределенность параметров процесса требует особых подходов при синтезе систем контроля и управления. В частности, для таких систем естественным образом необходимо применять распределенный контроль и распределенное управление [1–3, 10, 11].

В статье рассматривается задача оптимального управления процессами с рециркуляцией взаимодействующих потоков в ректификационных колоннах. Рециркуляция приводит к тому, что одни и те же управления как граничные, так и «объемные». Поэтому для вывода необходимых условий оптимальности здесь непосредственно применяется метод вариаций; управления предполагаются кусочно-непрерывными, а соответствующие им решения – непрерывными и кусочно-гладкими [1, 2, 11].

Постановка задачи

Рассмотрим следующую модель управляемого процесса:

краевые условия: ЩхХ! JW = k (y - y4x)) + F(t)Ф (l)x, dt       dl                                 F (1) -dim=(y*(x)-y), о

Начальные условия:

x(l,0) = x„(l), y(l,0) = y„(l), 0 < l< 1,

Xd(0) = Xd0, Xk (0) = Xk0, 0 < a, Ed< 1.

F(t) – поток в жидкой фазе, подводимый в колонну на промежутке l0 – σ ≤ l ≤ l0 + σ ; Фx(l) характеризует распределение потока по этому промежутку. Функция Фx может иметь, например, вид

CT 2

или

Фх (l)    e

CT²-(l -1₀)²

при при

I l - lc| < CT, I l - lg| - CT

Ф_х(1)=11^cos 0

²m [n (1 -1_o)] при |1 -1 o| < П = _а 2n

при 1 -10| > ст

.

Во втором случае m выбирается достаточно большим для обеспечения нужной гладкости Фx(l); в обоих случаях k выбирается так, чтобы

10 +ст

J Ф x (1) d1 = 1.

10 ст

Величины потоков при этом удовлетворяют условиям:

W⁽t)₊D⁽t)=F⁽t),      D⁽t)₊Ld⁽t)=V⁽¹, t),

W (t) + V (0, t) = L (0, t),   Vd (t) = V (1, t).

Предполагается, что удерживающие способности Hx, Hy постоянны, V не зависит от l, а L(l,t) имеет вид

L(l, t)

L (l, t) H

io_+CT

L (l, t) + F (t) J Фх (l) dl i о-a

при 1₀+ CT< l< 1

при 10 - CT < l < 10 + CT,

L(l, t) + F(t)

при 0 < l< 1₀- ct

что короче будем записывать таким образом:

L(l, t) = L(1, t)+L (l, t) = L(t)+L(l, t).

Такой вид L соответствует предположению, что изменение потока в жидкой фазе по высоте колонны происходит только за счет вводимого потока F(t). При этом условия (5) дают:

W (t) + D (t) = F (t),         D (t) + Ld (t) = V (t),

W (t) + V (t) = L (t) + F (t),   Vd (t) = V (t).

Из этих равенств следует, что Ld(t) = L⁽t) = ^L(1,t).

Анализ условий (5) показывает, что только два из четырех потоков W, D, L, V являются независимыми. Выбор тех или иных двух независимых потоков в качестве управлений опре-– 162 – деляет соответствующие задачи. Эти задачи, как задачи оптимального управления в классе кусочно-непрерывных управлений с критерием качества

T1

F = U (y (l, t) - 5* (l, t ))²dldt,

где θ^* – заданная функция.

Задача оптимального управления с управляющими потоками L, W

Здесь рассматривается задача оптимального управления, в которой управляющими параметрами являются потоки L = L(t) и W = W(t). Потоки V, D, L_d, V_d исключаются с помощью условий (5). Управления L, W выбираются в классе кусочно-непрерывных функций, принимающих значения в промежутках

L тп< L ( t) < L max,  W m< W ( t ) <W max,

поток F считается заданным. Переходя к нормальной форме дифференциальных уравнений, получаем следующую задачу:

t- ^(L+L )• 5(1) +IL

H

x₊ky (_y — y * '^

- X, x‘= 5 ^m.

^x                                                                                            (9)

y‘-W — l — f)• 5(2) + k (y• — y)]- y y-_ ^(2) о < t < t о < i < 1

t   Hy                          y                     l

при краевых условиях:

x'kt - -^[(L + F)x + (W - L - F)y - Wxk ] - Xk, Hxk y-a •[yk(xk)-xk]-xk -0, 0< t

x'dt - 7^[L + F — W](yd — Xd) - Xd,

Hx_d

(L + F - W) ■ (yd - y) - L(xd - x) = 0,

yd - y - Ed (y*( Xd) - y) = 0, о < t < T, l = 1, при начальных условиях (4) и ограничениях на управления:

(L -Lm,n) ■ (Lmax — L) — U2 = 0, ( W —Wmi^) ■ ( Wmax—W) — Z2 = 0.

Здесь u, z – вспомогательные управления.

Будем учитывать также ограничения на потоки D и V:

Dmin< D⁽t)< Dmax, где D ^{F W}, ^m_m< V⁽t) < Vmax, где V = ^{L + F - W}.

Из последних неравенств следует

Wmi

D F — W < D     F - D  < W < F — D ■ ,

min               max,           max              min ,

V •

Итак,

Wmin = max {Wmin, F - Dmax , F + Lmin - Vmax !<

~ max ,        min ,        max min m при условии, что любой элемент множества {Win,F—Dmax,F+Lmin - Vmax} не превосходит любой элемент множества {WL,,F—D-,.F+L — V-к Это означает, что параметры задачи max        min       max min должны удовлетворять условиям

Vmin < ^Lmax ^{+ D}max,  Vmax ~ ^Lmin ^{+ D}min,

а поток F должен удовлетворять следующим соотношениям:

F>W + D , min      min,

F max max,

F>W +V -T ^- Wmin  Vmin max,

F

+V max

L min

Будем предполагать, что эти условия выполнены. Заметим, что необходимость выполнения первых четырех из условий (13)–(14) естественно вытекает из первых двух условий (5).

Аналогично можно получить соотношение

LmnW) = max{L_, W - F+У^} < L(t) < min{Z^, W - F+VJ = L„(W) • (15)

При этом границы изменения W постоянны или определяются потоком F, а границы изменения L зависят от управления W. Получаем следующую задачу: для процесса, описываемого уравнениями (4), (9)–(11), в множестве кусочно-непрерывных управлений L, W, удовлетворяющих условиям

(W - Wmin)(^Wmax - W) - ^2 = 0, (L - Lm_m(W))(L_(W) - L) - U2 = 0,     (16)

найти такие, что соответствующее им решение задачи (9)–(11), (15), (16), (4) дает минимум интегралу (7).

Необходимые условия оптимальности

Для получения необходимых условий оптимальности рассматривается вспомогательный интеграл

I = I 1 + I2 = J J Ldldt +J J ^^t,

Q          6Q где L = (y-0^ + ^(1)(x‘-X) + ^(2)(x‘-Z(1)) + П1 (y‘-Y)+П(2)(У’-Z(2)),

%

% = A(‘)⁽x'kt^-Xk ) + At^{2) (}y^-xk^-a •⁽yk⁽xk ) ^-xk )) ⁺^d^{n (}x'dt^{- X}d ) ⁺

⁺^в^{2) ((L +}F^-W)•(y_d^-y^)-L(x_d^-x⁾⁾⁺x\^{3) (}y_d^-y^-Ed⁽y*_d^-y⁾⁾⁺/⁽(^{L - L}min^(W)).

(L max (W )-L ) - u 2 )+ .((W - W^mn )• Wmax - W )-^ 2 ) , где А1), А2), п(1), П(2) — функции, определенные на О = {(l,t) | 0 < l < 1, 0 < t < T}; 2^, 2^, у; s -функции, определенные на [0,T] (их можно считать определенными на dQ), причем

£ - Л^ - 0 на dQ/{(l,t) l - 0}, Y - 2d) = 0 на dQ/{(l,t)| l - 1}.

Пусть L, W – оптимальные управления; u, z – соответствующие им (согласно (16)) вспомогательные управления; x, y, x_k, x_d, y_d – оптимальное решение задачи (9)–(11), (4), отвечающее этим управлениям; δL, δW – вариации управлений L, W; δu, δz – вариации фиктивных управлений u, z, δx, δy, δx_k, δx_d, δy_d – соответствующие вариации решений. Пользуясь аргументацией теории вариационного исчисления, получаем необходимые условия оптимальности управляющих функций L и W: при 0 < t< T, 0 < l< 1

r- у r-kAy■)[r-n) x               1 x     ’;                                               (17) nt-FW *--k,fr - У 1+2(y - »'); Hy          I Hx Hy) при l = 0, 0 < t < T: r - A- = 0, r -1^ ■(L + F - W)- 2 = 0, \ H.     LHy H. J                               (18) -dt- = — 2k + 2k2,(-a(yk)'+ a - 1), 2k1(T) = 0; xk при t – T, 0 < l < 1: ξ = 0, η = 0;                                                                 (19)

при l = 1, 0 < t< T:

d2t;) = (L + HF- W) 2d - L2^, 2d (T) - 0, г             i xd HL + 2d2)• (L + F - W) + (1 - Ed )2d3) = 0,                               (20) :^^+«)].!=2rE.G■ *)= 0. Г22+2->l(L+F-W)-2=0; _ Hx    d J d d dd     , [ HXd      J                 d ’

при 0 < t< T:

1( ^              ^      21)                        21) j - I, x' ' il y'l dl -     (X(0, t) - y(0, t)) +т2 (yd - Xd ) + o ( x         y J        x                          xd                              (21) +2d2)(y (1, t) - yd + Xd - x(1, t)) - Y( Amn + Lmax - 2L) = 0, 1                               (1)                                      (1) j-nyd+Hk-(xk-y(0,t))-Hd-(yd-xd)-2d2(y(1,t)-yd)+ 0      y            xk                       xd                                                 (22)

+ 2W + Wax - 2W) = 0, yu = 0, ' = 0.                                    1     2     1     2 (3)

Так как уравнения (21), (22) определяют функции $, п, ^fc¹), ^к) ^d), "^О) ’ ^d полностью, то случаи, когда функции γ, ε равны нулю, связаны с дополнительными жесткими условиями на параметры задачи. Поэтому основным случаем следует считать тот, при котором z = 0, и = 0, Y ^ 0, е ^ 0, т.е. W = I¥_min, W = I¥_maxили W = F(t) + C1, где C 1 = const, L = Lm„, L = Lmax или L = –F(t) + C2, где C2 = const. Условия (13)–(14) можно использовать для построения областей значений оптимальных управлений. В частности, пусть

FUA^L -V ⁽⁾ mx mn ⁽⁾   mn, ⁽⁾ max ⁽⁾max   mn,

F(t) - D > F (t)+L - V

Область значений управлений W(t) для этого случая приведена на рис. 1. Пусть оптимальное управление W(t) имеет вид, представленный на рис. 2, соответственно этому управлению W(t) на рис. 3 приведена область значений управления L(t). Из этих двух рисунков следует:

• 1)    если W = Wmin, то

maX^{Lmin, Vmn ^{+ W}_mm — ^F(t^)}^ ™in{Lmax, ^Vmax ⁺Wrnn — ^F(t^)};

• 2)    если W = Wmax, то

max{Lmin, Vmrn + Wmax — F(t)}^ min{Lmax, Vmax + Wmax — F(t)};

• 3)    если W = F(t) – Dmax, то

max{Lmln, Vmn -Dmm}< L(t) < min{Lmax, Vmax — Dmax}.

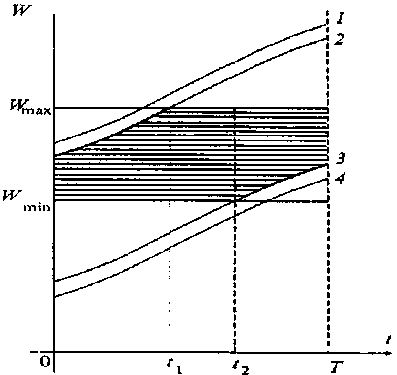
Рис. 1. Область допустимых управлений W: 1 – W = F – D_min; 2 – W = F+L_max – V_min; 3 3 – W = F – D_max; 4 – W = F + Lmin – Vmax

Fig. 1. The scope of admissible controls W: 1– W = F – D_min; 2 – W = F+L_max – V_min; 3 3 – W = F – D_max; 4 – W = F + Lmin – Vmax

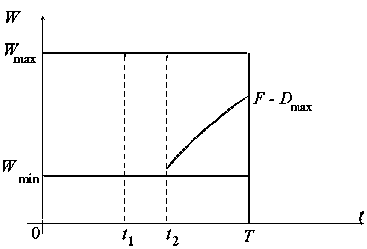
Рис. 2. График оптимального управления отбором внизу колонны

Fig. 2. Schedule optimal control selection column bottom

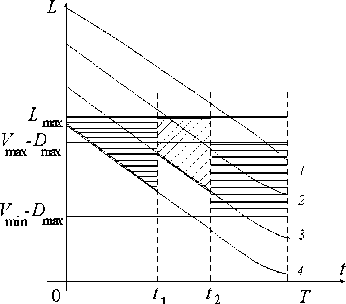
Рис. 3. Область значений управления L при оптимальном управлении W (см. рис. 2): 1 – L = V_max – F +W_max;

2 – L = V_max – F + W_min; 3 – L = V_min -F ₊W _max; 4 – L = V_min – F + W_min

Fig. 3. The range of values of control L with optimal control W (see Fig. 2): 1 – L = V_max – F +W_max;

2 – L = Vmax – F + Wmin; 3 – L = Vmin -F +W max; 4 – L = Vmin – F + Wmin

Пусть теперь график оптимального управления W(t) имеет вид, приведенный на рис. 4. Область изменения управления L(t) построена на рис. 5 при следующих условиях:

• 1)    если W = F(t) + Lmax – Vmax, то L = Lmax;

• 2)    если W = Wmax, то

max{^Lmin, ^V + ^Wmax - ^F(t ) ^L(t) ^ m^Lmax, ^Vmax ^{+ W}max - ^F(t^)};

• 3)    если W = F(t) – Dmax, то

max^{Lmin, ^Vmin - Dmax)} ^ L(t) ^ min^{Lmax. Vmax Dmax^}■

Разработанный метод оптимизации применен при автоматизации промышленных ректификационных установок сернокислотного алкилирования изобутана бутиленами, получения ортоксилола и др. [1, 3, 11].

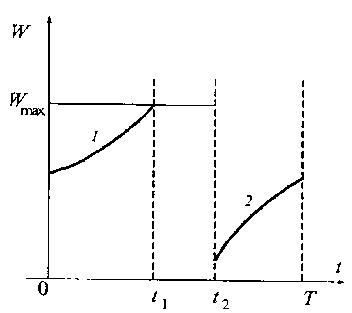
Рис. 4. График оптимального управления W:

1 – L = F + L_max – V_min; 2 – L = F – D_max

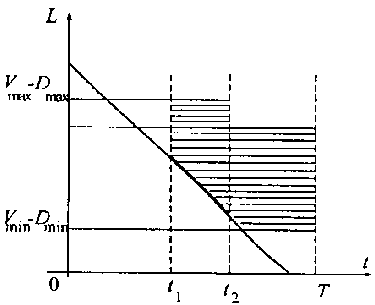
Рис. 5. Область значений управления

L = V_min – F + W_max при оптимальном управлении W (см. рис. 4)

Fig. 4. Graph of optimal control W: 1 – L = F + L_max – V_min;

2 – L = F – D

max

Fig. 5. Control Value Area L = V_min – F + W_max with optimal control W (see Fig. 4)

Благодарность

Исследование выполнено при финансовой поддержке РФФИ и Правительства Красноярского края в рамках научных проектов №№ 18-48-242001, 18-41-242004, 18-41-242008.