Оптимальное управление разведением спицы трансформируемого рефлектора при наличии возмущений

Космические антенны играют незаменимую роль в воздушно-космической связи, военной разведке, зондировании дальнего космоса, глобальном вещании, дистанционном зондировании Земли и прогнозировании климата. Из-за ограничений, накладываемых ракетоносителем, широко используются развертываемые антенны [1–3]. Они размещаются в обтекателе на этапе запуска, после выхода на орбиту начинается процесс развертывания и, наконец, образуются параболические отражающие поверхности. Стабильное и надежное развертывание рефлектора во многом обеспечивает успех космической миссии.

С конца 1960-х гг. крупногабаритные трансформируемые антенны стали активно применяться из-за их большой апертуры и малой массы. В настоящее время Astro Mesh рефлектор является наиболее совершенной и надежной из доступных развертываемых антенн [4; 5]. Процесс развертывания завершается фиксацией фермы и формированием необходимой формы отражающей поверхности.

Для подавляющего большинства таких конструкций раскрытие необратимо и отсутствуют эффективные способы обслуживания и активной корректировки на орбите радиоотражающего сетеполотна. Важно изучить и смоделировать процесс развертывания на стадии проектирования, чтобы получить глубокое представление о динамике развертывания [6]. Сложное кинематическое и динамическое поведение системы, высокие нелинейные напряжения и различные топологии кабельных сетей, а также рассеяние энергии, вызванное трением, демпфированием, и зазоры приводят к значительным воздействиям на динамику развертывания крупногабарит- ных трансформируемых антенн. Активно ведутся исследования в области динамического моделирования при раскрытии различных типов конструкций [7; 8].

Рассмотрим реализацию крупногабаритной космической конструкции с применением вантовой системы для создания необходимой формы радиоотражающей поверхности рефлектора (рис. 1) [9–12]. Крупногабаритный трансформируемый рефлектор (КТР) состоит из космического аппарата (КА) 1 . К нему прикреплены разворачиваемые элементы, такие как солнечные батареи 2 , облучающая система 3 . Для обеспечения заданной диаграммы направленности штанга 4 выдвигает рефлектор 5 на необходимое фокусное расстояние. Отражающей поверхностью является сетеполотно 6 .

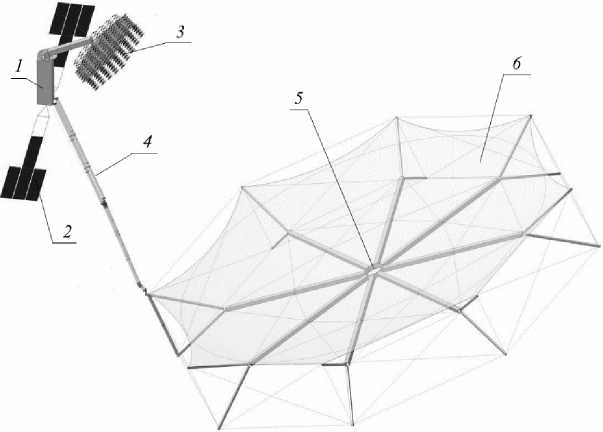
Рис. 1. Конструкция КТР

Fig. 1. The design of the LTR (Large-sized transformable reflector)

Важной проблемой при раскрытии КТР из сложенного положения в заданное с высокой точностью выхода к упорам является учёт возмущающих воздействий. Также необходимо плавно раскрыть элементы конструкции, так как с увеличением диаметра радиоотражающей поверхности возрастают моменты инерции антенны, что приводит к длительным затухающим колебаниям. Наличие радиации, большого перепада температур, солнечного ветра оказывает влияние на всю систему, и главным образом на диаграмму направленности [13; 14]. Поэтому необходимо решать задачи фильтрации и управления раскрытием рефлектора.

Математическое описание задачи

Рассмотрим процесс прямого раскрытия спицы КТР. Необходимо изменить положение спицы на заданный угол φ под действием силы М (рис. 2). Спица жестко закреплена одним концом к КА, вращение осуществляется под действием электрического двигателя.

Математическая модель, описывающая данный процесс, имеет вид X = f ( X , u , t ) + ξ x , где X = (φ ω a 1 V 1 a )^T – вектор состояния; ξ x = [ ξ x 1 ξ x 2 ξ x 3 ξ x 4 ]^T – воз-

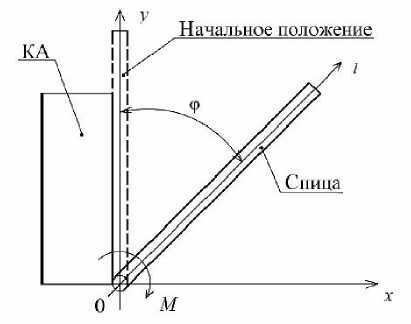
Рис. 2. Разведение спицы рефлектора

Fig. 2. Spreading of the reflector spoke

мущения с интенсивностью B x = diag ( B x 1 , B x 2 , B x 3 B x 4 ); u – вектор управления; t – время; φ – угол поворота спицы; ω – угловая скорость поворота спицы; a 1 и V 1 a – зависящие от времени изгиб и скорость изгиба спицы соответственно. В поэлементном виде система представляется следующим образом [15]:

ф = ®+^ x 1, a M (U, ф, ю) , е ю- I +S x 2,

+

2    M (U , ф , ю )

p Sb . ( L )      R d          4 ,

^( t ) = V a ( t ) + ^ x 3 ,

V1 a (t) =иг ^4 [ a1( t) + Y V1 a (t) ] p S    L             J где I – момент инерции спицы; E – модуль упругости; Iизг – изгибной момент инерции; ρ – плотность материала спицы; S – площадь спицы в поперечном сечении; l – координата длины спицы; γ – коэффициент затухания; M – общий момент, действующий на спицу: M(U, φ, ω) = Mп(U) – Mтр – Mупор(φ, ω) – Мф(φ, ω); Mп – полезный момент, создаваемый бесколлекторной машиной; U – напряжение питания бесколлекторной машины; Mтр – момент трения; Mупор – момент, создаваемый упором; Мф – момент, создаваемый фиксатором; h(t, l) = a1(t)b1(l) – изгиб спицы [10; 11; 15; 16]; a1(t) – функции только времени t; b1(l) – функции только координаты l; q1 = Z/L, где Z1 = 1,875, L – полная длина спицы; Rd – радиус вала двигателя.

Управление осуществляется за счёт изменения напряжения питания бесколлекторной машины U , | U | ≤ U max ( U max = 12,5 В). Полезный момент зависит от управления U [10] M п = m ф pE 0 U sin 9 / (м_р % c ), где m ф - число фаз ротора; p - число пар полюсов магнитного поля; E 0 - действующее значение электродвижущей силы (ЭДС) на обмотке статора; 9 - угол рассогласования (между U и E 0 , для двигателя находится в пределах [0, π/2])); ω p – угловая скорость вращения ротора двигателя; X c – синхронное сопротивление.

Рассмотрим спицу как цилиндрическую трубу. Примем её за однозвенную конструкцию. Измерению доступны угол поворота спицы и изгиб на ее конце. Для задачи разведения спиц уравнения наблюдения рассмотрим в виде z = h ( x, t ) + ^ z ,

где z = [ z 1 z 2 ]^T, h ( x , t ) = [φ d ( L )]^T, ( d ( L ) = a( t ) b ( L )), ξ z = [ ξ z 1 ξ z 2 ]^T – случайные процессы типа белого шума с интенсивностью B z = diag ( B z 1 , B z 2 ).

В соответствии с принципом разделения, задаче управления предшествует задача оценивания вектора состояния по неполным данным, заданным уравнением (2) [17–19]. Оптимальную оценку можно получить с помощью фильтра Калмана, уравнения которого для данной задачи будут иметь вид dt -Ю + R11 Bz1 ( zl  *P) + R13 bl ( L ) Bz2 ( z 2

_

\ d),

dd ° = MM + R 21 B - ( z . - ф ) + R 23 b . ( L ) B z 2 (. ddt L ₌ V a + R 31 B z . ( Z 1 - ф ) + R 33 b l ( L ) b ; 2 (

z ₂

z ₂

ˆ

- d),

ˆ

- d),

dV ^ˆ

--= - —^ q 4 ( ^a 1 + Y V 1 a )+^777 _v+ dt       p S    ^v ' p Sb 1 ( L ) R_d

^{+ R} 41 ^Bz 1 ^{( z} 1 ^- *P ) ^{+ R} 43 ^b 1 ^{( L} ) ^Bz 2 ( ^z 2 ^{- d} ) ,

R = f x R + Rf T - Rh T B ^- 1 h x R + B x , R ( t о ) = R o .

Здесь

f x = d f / d x, h x = d h / d x, h x

0 0 b 1 ( L ) 0

	0	1	0	0
	0	0	0	0
f x =	0	0	0	0
	0 .	0	EI изг 4 - P S q1	EI И q i y p S

, Rii (t0 ) = 9^Xi, i = 1,n, остальные элементы матрицы начальных ковариаций ошибок оценивания принимались равными нулю.

Спица приводится в движение приводом, в качестве которого рассмотрен бесколлекторный электродвигатель Phytron серии phySPACE [20]. Точность 3–5 % для 1,8º. Для измерения прогиба спицы h используется лазерный сканер RangeVision Standard Plus с точностью ±0,03 мм [21]. В качестве датчика углового положения используется энкодер ЛИР-МА208 [22] с точностью ±1º.

Требуется перевести спицу из начального положения X (0) = (0 0 0 0)^T в конечное X ( t f ) = (π/2 0 0 0)^T с отсутсвием перерегулирования по углу разворота φ за время t f = 90 c при наличии внешних возмущений ξ x и шумов измерений ξ z .

Постановка задачи управления

Рассмотрим иерархию целевых функционалов вида

J , = V f 1 ( X , t f ),                                           (5)

t f

J 2 = V f 2 ( X , t f ) + J [ f 0 ( X , t) + 0,5( u ² + u 0 )² k -2 ] dt ,                       (6)

t ₀

где V f 1 = 0,5β 1 [ω( t f ) – ω f ]²; V f 2 = 0,5Δ X f ^T ρ k Δ X f ; f 0 = 0,5β 2 [φ( t ) – φ f ]² + 0,5β 3 h ²; α = diag (α 1 , α 2 , α 3 , α 4 ); β 1 , β 2 , β 3 , k – заданные коэффициенты; Δ X f = X ( t f ) – X f , X f = (φ f ω f a 1 f V 1 af )^T – заданные конечные значения соответствующих переменных в (1). Так как h ( t , L ) = a 1 ( t ) b 1 ( L ), V 1 a ( t , L ) = V 1 a ( t ) b 1 ( L ), то a 1 ( t ) = h ( t , L )/ b 1 ( L ) и a 1 ( t f ) = h ( t f , L ) / b 1 ( L ).

Решение задачи управления разведением спицы по иерархии критериев в детерминированной постановке подробно представлено в работе [16]. Задача управления также решалась алгоритмами управления по принципу максимума с использованием численных методов Ньютона и Крылова – Черноусько, алгоритмом на основе ПИД-структуры регулирования, алгоритмом коррекции параметров структуры управления [10; 11; 15]. Применение алгоритма последовательной оптимизации по иерархии целевых критериев позволяет решать задачу в режиме реального времени с отсутствием длительных затухающих колебаний после достижения спицей заданного угла разворота. С помощью данного алгоритма удаётся добиться необходимой точности и качества регулирования системы.

Моделирование

Примем время раскрытия спицы tf = 90 с, максимальная допустимая амплитуда прогиба hmax = 10 мм. Значение коэффициента затухания γ = 0,04 с. Число фаз ротора mэ = 2, число пар полюсов магнитного поля p = 2, действующее значение ЭДС на обмотке статора E0 = 2,5 В, синхронное сопротивление Xc = 22∙10–3 Ом, угол рассогласования между полем ротора и статора 3 = п/10 при любой нагрузке, top =247 рад/с.

Были приняты следующие параметры спицы при моделировании [10]: материал АБС пластик QHF – 0140: плотность материала ρ = 1600 кг/м³, модуль упругости (Юнга) E = 1,2∙10¹¹ Па, длина спицы a = 9,75 м, масса спицы (всех вложенных звеньев) m = 32 кг. Рассматривается спица с сечением в виде кольца с внешним радиусом R = 0,26 м и внутренним радиусом r = 0,25 м. Момент инерции I будет равняться I = mR 2 /2 + ma 2 /3 = 1015,4 кг • м². Изгибной момент инерции I изг = π R ³δ = 5,52∙10^–4 м⁴, где δ – толщина стенки трубы (спицы).

Примем, что возмущения не превышают ±1 % от максимальных значений соответствующих переменных. В расчетах шумы ξ x и ξ z принимались белыми с интенсивностями B x = diag (0,02, 0, 0.0001, 0), B z = diag (0,02, 0,0005) соответственно. Начальные значения ошибок оценивания задавались в виде: <р( t ₀) = ф( t ₀) + А ф( t ₀), to( t ₀) = to( t ₀) + A to( 1 ₀), a 1 ( t ₀) = a 1 ( 1 ₀) + А a 1 ( 1 ₀), V a ( 1 0 ) = V a ( 1 0 ) + А V a ( 1 0 ), где Аф( 1 0 ) = 0,1 рад, Ato( 1 0 ) = 0,002 рад/с, A a i ( 1 0 ) = 5 • 10^-5 м, Δ V 1 a ( t 0 ) = 0,01 м/с.

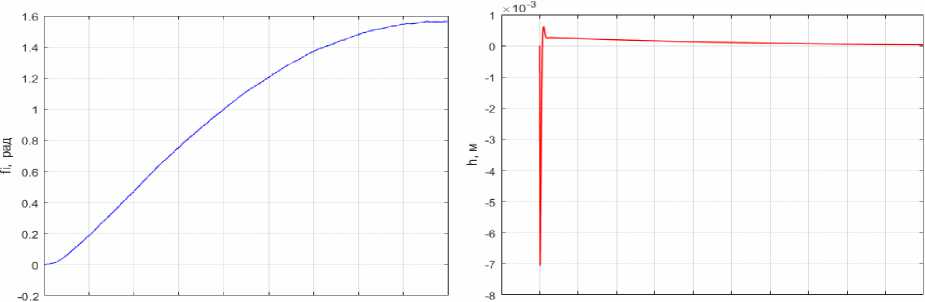
На рис. 3 представлены результаты моделирования: графики зависимостей φ( t ) (на всем интервале оптимизации) и h ( t ) (на первых 10 с). Видно, что удалось решить поставленную задачу, т. е. раскрыть спицу из начального положения на заданный угол π/2.

O 10     20     30     40     50 во /□     80     90      -1     0     1     2     3     4     5     6     7     8     9    10

t. c                                                                                                               t, c а                                             б

Рис. 3. Графики: a – φ( t ); б – h ( t )

Fig. 3. Graphics: a – φ( t ); b – h ( t )

Максимальный прогиб спицы h ( t ) = 7∙10^–3 м наблюдается в начальный момент времени, в дальнейшем он плавно стримится к нулю. При использовании алгоритма последовательной оптимизации по иерархии из двух целевых критериев механизмы упора и фиксатора из-за плавного подхода к конечному состоянию не приводят к дополнительным колебаниям развернутой антенны.

При выбранных возмущениях и шумах измерений алгоритмы оптимальной фильтрации и управления успешно решают поставленную задачу. Отклонения начальных значений переменных величин допустимо выбирать из диапазона ±7 % от максимальных значений соответствующих величин, в противном случае требуется корректировка весовых коэффициентов.

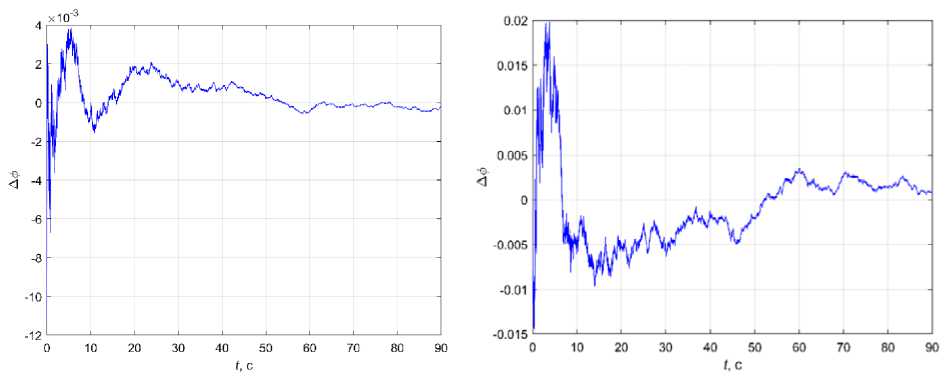
На рис. 4, а показан график изменения ошибки оценивания Δφ при Bz = diag(0,02, 0,0005) и при отсутствии внешних возмущений. На рис. 4, б показана аналогичная кривая при увеличении интенсивности Bz втрое. Наибольшая ошибка достигается в начале моделирования, затем она стремится к нулю (в том числе и для других Δφ(t0)). При наличии внешних возмущений ошибки имеют математическое ожидание равное нулю и дисперсию, не превышающую дисперсию возмущений.

б

а

Рис. 4. Графики Δφ при различных уровнях интенсивности шума

Fig. 4. Graphics of Δφ at different levels of noise intensity

На рис. 5 представлены диагональные элементы матрицы ковариации при R 11 (0) = 0,017; R 22 (0) = 0,0002; R 33 (0) = 0,001; R 44 (0) = 0. Достаточно быстро они приходят к установившемся значениям. Было проведено моделирование при различных начальных значениях диагональных элементов матрицы ковариации и разной интенсивности шумов измерений, фильтр Калмана успешно отработал все варианты.

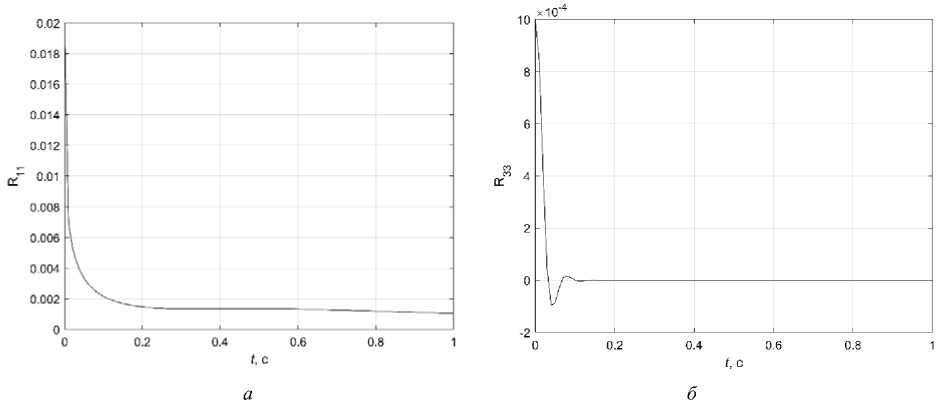
Рис. 5. Графики: а – R 11 ( t ); б – R 33 ( t )

Fig. 5. Graphics: a – R 11 ( t ); b – R 33 ( t )

Для минимизации энергетических затрат было предложено периодически отключать работу датчиков и оценку состояния на этих участках вычислять путем прогнозирования с использованием уравнений (3), (4) при B Z1 = 0 и В - = 0. Это позволило успешно решать задачу управления при меньших энергетических затратах. При отключении датчиков не затрачивается энергия на их функционирование и передачу данных.

На рис. 6 представлен график R 11 ( t )

4 =- R 112 B z 1 ^{- 1} — R 132 b. B z 2 - 1 + 2 R 12 + B x 1

при периодическом отключении измерений с датчиков. Каждый раз при включении измерений элементы ковариационной матрицы достигают установившегося значения. В уравнении для R 11 слагаемые R 11 ² B z 1 ^{- 1} и R ₁₃ ² b 1 B z ₂ ^{- 1} характеризуют скорость поступления информации, их отсутствие при отключении измерений приводит к возрастанию R 11 .

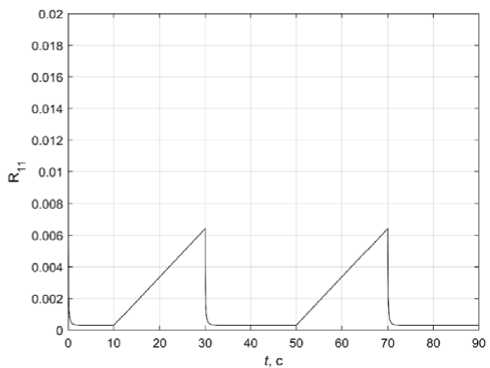
Рис. 6. График R 11 ( t )

Fig. 6. Graphic R 11 ( t )

Для успешного решения задачи и точного выполнения терминальных условий необходимо включение датчиков измерения состояния системы на конечном отрезке интервала оптимизации. Чем больше время включения датчиков в конце моделирования, тем точнее удаётся решить поставленную задачу. Определение оптимального интервала включения измерений является самостоятельной научно-технической задачей. При возрастании интенсивности внешних возмущений B x необходимо измерять состояние системы более длительное время. При заданном B x = diag (0,02, 0, 0,0001, 0) для успешного решения задачи достаточно включения датчиков на участке с 85 по 90 с. При увеличении значений возмущений вдвое необходимо увеличить время наблюдений на конечном участке до 15 с. Время работы датчиков зависит от вида и интенсивности внешних возмущений, требований к величине допустимых энергетических затрат. В результате статистического моделирования оценка математического ожидания критерия (5) M ( J 1 ) = 0, критерия (6) M ( J 2 ) = 0,035, где для одного из вариантов получено следующее значение φ( t f ) = 1,576.

Отдельной задачей стоит определение времени отключения датчиков измерения углового положения спицы и величины прогиба независимо друг от друга. Так, для выполнения терминального условия по углу φ при заданных возмущениях необходимо осуществлять наблюдение последние 5 с моделирования, тогда как для выполнения требований для прогиба h достаточно 3 с наблюдений. Величины φ и h зависят от приложенного момента М . Значение h в конце раскрытия при выбранном управлении не превышает 5∙10^–5 м, что соответствует точности датчика. Поэтому значением прогиба в конечный момент времени можно пренебречь.

Заключение

В результате проделанной работы было подтверждено решение задачи оптимального управления стохастической моделью раскрытия спицы КТР по неполным данным с использованием принципа разделения. Использование алгоритма последовательной оптимизации при полученных оцененных с помощью фильтра Калмана данных позволило решить поставленную задачу при различных интенсивностях возмущений и шумов измерений. Интервальное выключение измерений позволяет снизить энергозатраты на питание датчиков и обработку измерений. Дальнейшие работы предполагают поставить и решить задачу оптимизации интервалов наблюдений для минимизации энергетических затрат [23].

Представленные исследования доложены на XXII Международной научной конференции «Системный анализ, управление и навигация» [24].