Оптимальное управление температурой и расходом теплоносителя в тепловых сетях при переменном кпд насосов

В работах [1–3] рассматривались варианты решения задачи оптимального управления температурой и расходом теплоносителя в системах теплоснабжения, т. е. решалась задача оптимизации так называемого количественно-качественного регулирования процесса [4]. Причем в первом варианте задача заключалась в оптимизации процесса простого переноса тепловой сетью заданного количества теплоты [1]. При этом не учитывались ни характеристики теплопотребляющего оборудования, ни само значение теплоты, собственно необходимое потребителю, а также требуемая температура микроклимата зданий. Поэтому применительно к тепловым сетям реализация решения такой задачи оптимизации приводит к определенным сложностям. Здесь следует отметить, что для тепловых сетей прежде всего важна не просто теплота, переносимая в целом через поперечное сечение теплопровода, а то ее количество, которое мо- жет быть «снято» с теплоносителя оборудованием отапливаемых зданий и которое должно быть достаточно для поддержания заданного микроклимата в них. Все это учтено во втором варианте решения задачи [2, 3], однако при этом в обоих вариантах считалось, что коэффициент полезного действия (КПД) сетевых насосов является постоянной величиной. Вместе с тем достаточно хорошо известно, что КПД как сетевых, так и любых других насосов зависит как от подачи – расхода перекачиваемой среды, так и от частоты вращения ротора электродвигателя. Конечно, иногда ситуация может оказаться такой, когда за счет изменения числа и схемы включения задействованных насосов, как нерегулируемых, так и с частотным электроприводом, удается обеспечить их работу в номинальном режиме и обеспечить постоянство КПД всей насосной станции [5–7]. Так, например, при равенстве относительной частоты вращения ротора электродвигателя насоса его относительной подаче КПД будет постоянным и равным своему номинальному значению [7].

КПД частотно-регулируемого насоса ] н , как известно, определяется следующим соотношением:

П н = П ном [1 - ( G / ^G hom ^Ю / Ю ном ) ² ( ^Ю / Ю ном ) 2 ^] . (1) Если при этом относительная частота вращения ротора электродвигателя ю / ю _ном будет выбираться равной его относительной подаче G / G _Hom , то КПД насоса будет равным своему номинальному значению п _ном . Однако при этом напор, развиваемый насосом должен быть достаточным для прокачки через тепловую сеть расхода G, т. е. должно выполняться следующее равенство:

H = Н 0 ( ю / Ю ном ) ² - 5 в G ² = 5 н G ² .         (2)

Отсюда следует, что сопротивление нагрузки (тепловой сети) 5 _н должно быть только таким: 5 _н = Н 0 / G 1_om - 5 в ; в других случаях добиться того, чтобы п _н = П _ном можно только с определенной [6, 7] погрешностью и, как указано в [8], «…при этом КПД установки изменится незначительно». Как известно, для практики должно быть так: Н / G²  > 5 „ + 5„ , иначе нет возможности

0    ном    н    в регулировать подачу теплоносителя.

Здесь H ₀ – напор холостого хода, развиваемый насосом при номинальной частоте вращения ю _ном, S _в - его внутреннее сопротивление, ю - фактическая частота вращения ротора электродвигателя или, что то же самое, рабочего колеса насоса, G и G _ном – соответственно фактический и номинальный расходы теплоносителя. Очевидно, что данное соотношение выполняется как для массовых, так и для объемных расходов теплоносителя.

Таким образом, решение задачи оптимального управления теплоснабжением, рассмотренное в работах [1–3], имеет определенное практическое значение. Тем не менее специалистам достаточно интересно было бы знать, как изменится это решение, если учитывать зависимость КПД сетевых насосов от подачи. Заметим, что в данном случае речь идет только об использовании нерегулируемых насосов с постоянной частотой вращения рабочего колеса – это наиболее часто встречающийся случай для систем теплоснабжения. Эта проблема и исследуется в настоящей работе.

Постановка задачи

Как известно [9–12], зависимость КПД насоса от его подачи – расхода перекачиваемой среды при номинальной частоте вращения может быть представлена следующим соотношением:

П н = И ном ^- (1 ^{- G} / ^G hom ) ² И ном .              ⁽³⁾

Учтем это соотношение при решении задачи об оптимальном управлении температурой и расходом теплоносителя в тепловых сетях [2, 3].

Электрическая мощность W э , необходимая для перекачки сетевой воды на расстояние 1 м, как это хорошо известно [см., например, 4], вычисляется по следующей формуле:

W₃ = 0,88 к⁰²⁵G 3 (1 + a )/( D :H" p ' n 'T_L i _n , ),  (4)

где k э – эквивалентная шероховатость внутренней поверхности теплопровода, D вн – его внутренний диаметр, р - массовая плотность теплоносителя, G m - его массовый расход, п э — КПД электродвигателя насоса, а - доля местных потерь давления (потерь давления из-за местных сопротивлений). Также известно [9, 10], что КПД электродвигателя можно принять постоянным и равным его паспортному значению.

Если в данное уравнение подставить соотношение (3), то оно перепишется в виде

W ₃ = 0,88 k₃⁰’²⁵G² (1 + а ) g Hom /

/[^рУП ном П э ( 2 G hom — G m ) ].      (5)

Потери теплоты одним погонным метром подающего теплопровода в окружающую среду за единицу времени определяются линейной плотностью теплового потока q ^ :

q i   ^п < t пр ^- 1 ну R i ,                              (6)

где t пр – температура теплоносителя в подающем теплопроводе, t н – температура наружного воздуха, R l – линейное термическое сопротивление теплопередаче теплопровода [13, 14].

Следовательно, суммарные затраты (потери) энергии (тепловой и электрической) WΣ в единицу времени (мощность потерь-затрат), приходящиеся на один погонный метр теплопровода, будут равны w =    0,88к025Gmm (1 + а) Gh2om    +

^Z   [ D^p² П ² П ном П э ( ^{2 G} hom ^- G m ) ]

+ ^{П (} t пр - t н ) .                                   (7)

R l

Известно, что цены на электрическую и тепловую энергии различные, и понятно, что минимизировать следует не сами потери энергии, а их стоимость. Поэтому перед вторым и третьим слагаемыми в формуле (8) укажем коэффициент р , который представляет собой отношение цены на тепловую энергию к цене на электрическую, и обозначим полученную таким образом величину – относительную стоимость потерь энергии – неким критерием I :

_{1 =}     0,88 к °’²⁵ G m ( 1 + а ) G _h²o_{M    +}

[ ^ в⁵Н2⁵ р ² П ² П ном П э ( ^{2 G} нoм ^- G m ) ]

(11). При этом вполне понятно, что при постоянной температуре наружного воздуха теплота, необходимая объекту W _об, тоже является постоянной величиной для заданного значения t в , причем независящей от режима теплоснабжения . Поэтому вполне обоснованно считается, что для указанных погодных условий ^ об = const и задача управления теплоснабжением заключается в выборе соответствующих значений G m и t пр .

Используя соотношения (9) и (10), получим, что tобр = tпр - Woб / (cGm )’                     (12)

Р ^п ( t пр ^- t н )

⁺ R

Таким образом, следует минимизировать критерий I за счет выбора расхода G_m и температуры t _пр теплоносителя в подающем теплопроводе. Причем при этом следует иметь в виду, что переменные G m и t пр не являются независимыми величинами, а связаны между собой неким соотношением, обусловленным тем, что при надлежащем теплоснабжении количество теплоты, которое будет «снято» с теплоносителя оборудованием отапливаемых зданий, должно быть достаточным для поддержания заданного микроклимата в них. По-

О_т = W oб /[2 с ( t пр - 1 в - W oб / KF ) ].       (13)

Кроме того, для упрощения дальнейших выкладок введем следующие обозначения:

a = 0,88 k   ( 1 + а ) G^m /( Л ^лЧ ом П э );

b = рп / R l ; s = -pn t _H / R l .

С учетом этого, а также формулы (12) критерий I перепишется в виде

I =------ m ---+ bt^ + s .                 (14)

пр

^{2 G} нoм   G m

Таким образом, формально задача оптимиза-

ции запишется так:

этому установим это соотношение.

Для теплоты, потребляемой объектом теплоснабжения, как известно, выполняются следующие соотношения:

I =

aG m

2 G нoм - G m

^{+ bt} пр

+ S ^

min

.

G m ’ t пр G П

Множество Ω, как это следует из уравнения (13), определяется соотношением:

W o6 = cG m ( t пр - 1 обр ) ,

W o6 = KF [( t пр + t обр )/2 - t в ] . (10) где W об – теплота, потребляемая объектом теплоснабжения в единицу времени, c – удельная теплоемкость теплоносителя, KF – произведение коэффициента теплопередачи на площадь поверхности теплообмена (в данном случае объект теплоснабжения представляется эквивалентным отопительным прибором) [15–17], t _обр – температура воды в обратном теплопроводе, t в – температура внутреннего воздуха зданий.

При этом следует иметь в виду, что теплота W об , необходимая объекту для поддержания заданного микроклимата (в данном случае заданной температуры внутреннего воздуха), в соответствии с физикой процессов теплообмена вычисляется по формуле

W oб = q v V ( t в — t н ) . (11)

Как видно из (11), эта величина определяется только теплозащитными свойствами зданий – их удельной тепловой характеристикой q_v , их общим объемом V , а также температурами внутреннего t в и наружного воздуха t н .

Система теплоснабжения должна работать так, чтобы с помощью существующих систем отопления зданиям в целом доставлялось такое коли-

« = ^ G m , t пр Ю,

—

W об

2 c ( t _П р - 1 в - W * / KF )

= 0

Решение задачи

Используя метод подстановки и выражая расход теплоносителя через его температуру в подающем теплопроводе (см. формулу (13)), свели вышеприведенную условную задачу оптимизации к безусловной задаче минимизации по переменной t _пр:

I = aW 06 x [8 c ² О ном ( t пр - t_e - W oб / KF ) ² -

-2 cW oб f t пр - 1 в - ^{W o}б ) ] - ¹ + S + bt пр ^ min . (17)

V         KF )                t пр

Если ввести обозначение у = t _в + W_oб / KF , тогда задача оптимизации перепишется в виде

I = aW 0б х [8 c ² G нoм ( t пр -у )² -

^{-2 с} ^ ,б ( t пр ^-y ) ^{] 1 + s + bt} пр ^ min .      ⁽¹⁸⁾

t пр

Решая данную задачу методом производной, найдем, что точка, «подозрительная на экстремум», должна удовлетворять следующему уравнению:

d^- = - aW o ² б Х [16 с ² G нoм ( t пр -Y ) - 2 cW oб ] х dt _пр

чество теплоты, какое получается по соотношению

^ [8 с ² С ном ( t пр -Y )² - 2 cW oб ( t пр -Y ) ] - ² + b = 0 . (19)

Отсюда следует, что координаты критических точек следует искать из решения уравнения 32 c ³ g Hom b ( t пр -Y )⁴ - 16 cW G hom b ( t пр -у )³ + + 2 cW£b ( t пр -у )² - 8 acW 2 G _HO m ( t пр -y ) + aW j, = 0 . (20)

Если ввести обозначение t пр - y = x , то уравнение (20) перепишется в виде

32c3gHombx4 -16cWGhombx3 +

+ 2 cW 2 bx ² - 8 acW об G hom x + cW = 0.     (21)

Таким образом, решение данной задачи приводит к необходимости отыскания корней полного алгебраического уравнения четвертой степени. Если же считается, что КПД сетевых насосов постоянен, то задача значительно упрощается и, как показано в работах [1-3], сводится к нахождению корней двучленного уравнения четвертой степени.

Для расчетной температуры наружного воздуха в –34 °С и объекта теплоснабжения с расчетной тепловой нагрузкой в 35,7 МВт, с расчетными температурами теплоносителя 95/70 °С, используемыми при проектировании систем отопления зданий, определили оптимальные температуры теплоносителя в подающем и обратном теплопроводах и оптимальный его расход. При этом численные значения других параметров объекта теплоснабжения были следующими: Dвн = 514 мм; кэ = 0,5 мм; ПэПном = 0,65; a = 0,22; Ri = 2,04 м-°С/Вт; tв = 20 °С. Отношение цены на тепловую энергию к цене на электрическую было равно Р = 0,403. Произведение коэффициента теплопередачи на площадь поверхности теплообмена для всего объекта теплоснабжения KF определялось по формуле, приведенной в работах [2, 3]. Точнее этот комплексный параметр может быть определен по эксплуатаци- онным данным, например, методом наименьших квадратов [18]. Номинальный расход (подача) насоса считался равным Gном = 337,43 кг/е~1250 м3/ч.

Для решения полного алгебраического уравнения четвертой степени (21) использовали специальные онлайн-калькуляторы [19, 20]. При этом, как и должно быть, получали два комплексных и два действительных, причем положительных значения корня. Для ответа всегда оставляли большее поло- жительное значение, так как при использовании другого положительного значения оптимальный расход теплоносителя кратно превышал номиналь- ную подачу насоса, что практически невозможно.

Поэтому область допустимых решений Q следует дополнительно       ограничить

0 <  G m <  G™ , т. е. должно быть так:

Q = условием

G m , t пр | G m

^W об

• ² c I t пр ^- t в

U0 < Gm < G™

----X = 0

W o6 )

KF J

На рис. 1 и рис. 2 приведены графики оптимальных кривых для температур и массового расхода теплоносителя в зависимости от температуры наружного воздуха. Как видно из рис. 1 и рис. 2 оптимальные значения параметров теплоснабжения заметно отличаются от проектных, так, в частности, при t _н =-34 °С оптимальная температура теплоносителя в подающем теплопроводе должна быть почти на 10 °С выше расчетного значения в 95 °С, а оптимальный расход существенно ниже расчетного значения в 340 кг/с. Объясняется это, очевидно, относительно высокой (более чем в два раза) стоимостью электрической энергии.

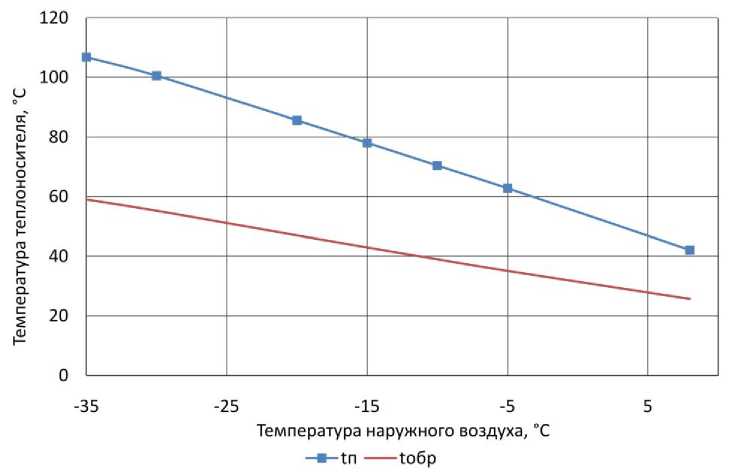
Рис. 1. Графики оптимальных температур теплоносителя в зависимости от температуры наружного воздуха

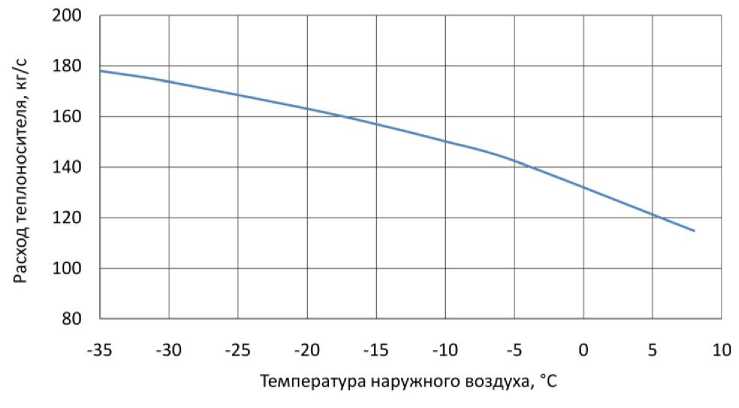
Рис. 2. Изменение оптимального расхода теплоносителя в зависимости от температуры наружного воздуха

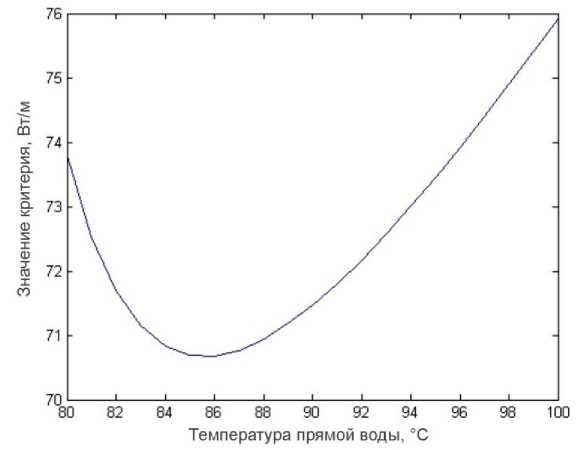
Рис. 3. Изменение критерия I в зависимости от температуры теплоносителя в подающем теплопроводе

Как видно также из рис. 1 и 2, оптимальные температуры и расход имеют совершенно разные значения для разных температур наружного воздуха. Исходя из этого, следует сделать однозначный вывод о том, что в тепловых сетях разумно применять качественно-количественный метод регулирования, а не только качественный метод, как это принято в подавляющем большинстве случаев в настоящее время [4, 21].

Для подтверждения того, что при найденных параметрах достигается именно минимум используемого критерия (17), на рис. 3 приведена кривая изменения этого критерия в зависимости от температуры в подающем теплопроводе для условий теплоснабжения объекта при t _н =-20 °С. Как видно из рис. 3, при t _пр = 85,6 °С достигается именно локальный минимум этого критерия.

Выводы

Рассматривается задача управления процессом теплоснабжения по критерию минимума затрат электрической энергии на перекачку теплоносителя и сокращения тепловых потерь при его транспортировке по теплопроводам. Установлено, что для минимизации критерия следует применять качественно-количественное регулирование процесса теплоснабжения, т. е. при изменении температуры наружного воздуха необходимо изменять не только температуру теплоносителя, но и его расход.