Оптимальные и квазиоптимальные алгоритмы различения импульсных сигналов

Вопросы анализа потенциальной помехоустойчивости приема импульсных тональных сигналов кода Морзе на фоне белого шума рассматривались в ряде работ [1-4]. Однако, при этом предполагалось, что частота, амплитуда, длительность и время прихода сигнала точно известны, замирания отсутствуют и помехой является только белый шум. В настоящей работе находится структура оптимального приемника полностью известного сигнала, наблюдаемого на фоне белого шума, и выяснение основных особенностей процесса различения гипотез. После этого обобщается решение на случай замирающего некогерентного сигнала.

Синтез и анализ оптимальных алгоритмов

Рассмотрим статистический синтез оптимальных алгоритмов различения трех возможных гипотез для приема импульсных сигналов: H ₀ – отсутствие сигнала (пауза); H ₁ – передача сигнала «точка» длительностью τ ₀ ; H ₂ – передача сигнала «тире» длительностью 3τ ₀ . Будем считать, что принимаемый сигнал на интервале времени 0 ≤t≤T имеет следующий вид:

• -    при гипотезе H ₁

U ( t ) = U 1 ( t ) + n(t), U 1 ( t ) = U 0 cos ^ 0 t, 0 <  t <  т 0 ;

• -    при гипотезе H ₂

U(t) = U2 (t) + n(t), U2 (t) = U0 cos^0t, 0 < t < 3т0, где n(t) - белый шум со спектральной плотностью N0 . Предполагая, что априорные вероят- ности гипотез и потери, связанные с неверными решениями, одинаковы, приходим к следующему правилу различения сигналов. Вычислим апостериорные вероятности каждой из трех гипотез:

⎛ ^T          ⎞

P(U(t),0 <  t <  T ) = K o expl - — Ju ² (t)dt I,

⎝ ^N 0 0         ⎠

P 1 ( U (t),0 <  t <  T ) = K ₀ exp

⎛T

- IT J ( U (t) - U- (t) )

⎝ ^N 0 0

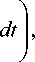
P , (U(t),0 <  t <  T ) = K o exp

⎛T

- 7Г J ( U (t) - ^U'(t ) )

⎝^N 0 0

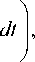
где K ₀ – коэффициент, не зависящий от номера гипотезы. Оптимальное байесовское правило принятия решения заключается в сравнении этих апостериорных вероятностей и выбора номера гипотезы наибольшего из чисел.

После элементарных преобразований рассмотренная процедура приводится к следующему виду. Найдем по реализации U ( t ), 0 <  t <  T два числа

L = 0 U ( t )U, ( t ) dt -¹ 0 U 2 ( t ) d[t, ОО                     2 0

3τ 0                          3τ 0 (1)

L₂ = Ju ( t ) U₂ ( t ) dt — Ju 2 ( t ) dt .

0                 2 0

Гипотезы    H0 , H1 или H2 выбирают ся соответственно большему из трех чисел

L ₀ = 0, L 1 или L 2 .

Определим вероятностные характеристики оптимального алгоритма различения сигналов. Найдем условные математические ожидания и дисперсии статистик L ₁ и L ₂ при гипотезах H ₀ ,

H i и H 2 : M { L i /H 0 } = -E i , M^/H ₀ } = -3 ^ ,

M { L , /H i } = E , M { L /H i } = -2 E 1 , M { L i /H 2 } = E ,

M {L2 /H2} = 3E1. Апостериорные дисперсии ста тистик L1 и L2 при всех гипотезах одинаковы: ⎧⎛τ0                        ⎞2 ⎫ j"n(t)U0 cos a0td

D { L 1 } = M <

⎝ 0

⎬ = 0,5U 0² N 0 τ 0 ,

D { L 2 } = 0,5U o² N o 3 т 0 .

После выполненных преобразований найдем условные вероятности ошибочных решений. Для справедливой гипотезы H ₀ ошибка произойдет, если будет выполнено хотя бы одно из двух неравенств: L 1 >  0, L 2 >  0, т.е. вероятность ошибочного решения

P ( H 0 ) = P { L i >  0 } + P { L >  0 } -

- P { L 1 >  0, L 2 >  0 } ,

∞ где       P{L > 0} = Jto(L /H0) dL;

P { L 2 >  0 } = j ю ( L 2 /H 0 ) dL 2 ;

P { L 1 >  0, L 2 >  0 } = jj to ( L 1 , L 2 /H 0 ) dL 1 dL 2 ;

to ( L 1 , L 2 1H 0 ) — двумерная нормальная плотность распределения статистик при гипотезе H 0 , с найденными математическими ожиданиями, дисперсиями и ковариацией

B(L,LjНо) = M{(L -M{L/Но})х

х(L2 -M{L2IНо})} =

= M ^

τ ₀ τ ₀

J Jn(t)п(т)U02 cosro0t cos гоотdtdT

0∞

P { L 1 <  0, L 1 <  L 2 } = J J to ( L 1 , L 2 /H 1 ) dL 2 dL 1 .

-∞ L ₁

Числовые характеристики нормального распределения to ( L 1 , L 2 (H_x ) находятся аналогично. Наконец вероятность ошибочного решения при условии справедливости гипотезы H ₂ находится с помощью следующих соотношений

P (H2) = P {L2 < 0} + P {L2 < L1} -

- P { L 2 <  0, L 2 <  L 1 } ,                      (4)

где P { L 2 <  0 } = J ro ( L 2 /H 2 ) dL 2 ,

-∞

P { L 2 <  L 1 } = J J ro ( L 1 , L 2 /H 2 ) dL 1 dL 2 ,

-∞ L ₂

0∞

P { L 2 <  0, L 2 <  L 1 } = J J ro ( L 1 , L 2 /H 2 ) dL 1 dL 2 .

-∞ L ₂

Полученные результаты позволяют провести анализ вероятностей ошибок для случая полностью известного сигнала, т.е. определить потенциальные характеристики алгоритмов различения импульсных сигналов. Основной энергетической характеристикой такой системы является отношение сигнал/шум, приведенное, например, к сигналу «точка»:

_ (M№0})2 _ ид q      d{l}      8N0 .

По полученным формулам (2) - (4) были построены графики зависимостей вероятностей правильного решения гипотез H 0 , H 1 и H 2 от отношения сигнал/шум, которые представлены на рис. 1.

= 0 , 5U о² N o T 0 .

Таким образом, полученные формулы позволяют найти вероятность ошибочного решения при гипотезе H 0 . Точно так же для гипотезы H 1 вероятность ошибочного решения можно определить по формуле

P(Hi) = P{L < 0} + P{L < L2} -

- P { L <  0, L <  L 2 } ,

∞ где      P{L1 < 0} = Jю(L1 /H1)dL1,

∞∞

P { L 1 <  L 2 } = J J to ( L 1 , L 2 [H 1 ) dL 2 dL 1 ,

-∞ L ₁

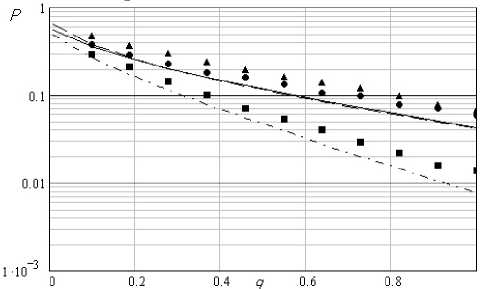
Рис.1. Зависимости вероятностей ошибочного решения от уровня полезного сигнала для гипотезы H ₀ (сплошная линия), H ₁ (пунктирная) и H ₂ (штрих-пунктирная)

Так же на этом графике представлены вероятности ошибочного решения, полученные на основе моделирования работы оптимального алгоритма различения сигналов. На графике кружками показана вероятность ошибочного решения для гипотезы H 0 , треугольниками - для гипотезы H 1 , квадратиками - для гипотезы H 2 .

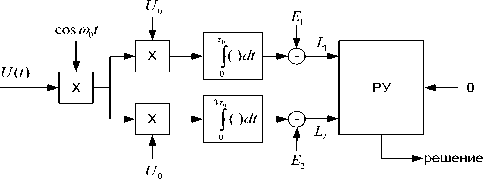
Рис. 2. Корреляционный приемник известных сигналов

Существует два варианта технической реализации найденного правила различения сигналов на основе корреляционного приемника или согласованных фильтров. В первом случае схема содержит синхронный детектор, два коррелятора, вычитающее и решающее устройство (РУ). При этом осуществляется вычитание половины ожидаемой энергии

• 1    Т

E = - JU 12 (t)dt = -( U о2 т о /2 ) ,

• 2    0

3τ 0

e₂ =- Ju 2 ( t ) dt = -(u 2 3t₀ /2)

• 2    0

из корреляционного интеграла. Фильтровой вариант реализации предполагает наличие двух фильтров (СФ1 и СФ2), согласованных с прямоугольными импульсами длительностью τ ₀ и 3τ ₀ .

E 1

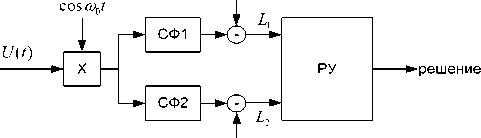
E 2

Рис. 3. Оптимальный прием известных сигналов на основе согласованной фильтрации

Был предложен квазиоптимальный алгоритм различения элементов кода Морзе, который представлен на рис. 4.

Элементы кода Морзе представляются в виде ШИМ-сигнала. Тогда при дешифрации требуются измерения четырех интервалов времени: длительности символов «точка» (T) и «тире» (3T) длительности бестоковых посылок между бук- вами (3T) и словами (5T) . Для определения границ импульсов и пауз следует воспользоваться классическим правилом измерения длительности одиночного импульса (по уровню 0.5 от амплитуды импульса).

Поскольку вершины импульсов и бестоковые участки под воздействием шума имеют значительную нестабильность, то следует определить наиболее вероятное значение амплитуды импульсов. Для этого строится гистограмма входного сигнала, по которой и определяется амплитуда ШИМ-сигнала. Нахождение уровня равноотстоящего от вершины импульсов и их основания позволяет определить длительность символов «точка» и «тире», а так же длительности бестоковых посылок между буквами и словами.

Измерив параметры ШИМ-сигнала, можно представить его в виде АИМ-сигнала, амплитуда которого определяется площадью импульсов ШИМ-сигнала. Таким образом, амплитуда АИМ-сигнала пропорциональна длительности элементов кода Морзе. Переход к АИМ-сигналу позволяет сформировать вектор, элементами которого являются длительности элементов кода Морзе.

Для принятия решения о том, что принятый сигнал является сигналом с кодом Морзе, следует определить ошибку отклонения символов «точка» с длительностью T , символа «тире» с длительностью 3 T , бестоковой посылки между символами с длительностью T и бестоковой посылки между буквами с длительностью 3 T от ожидаемых значений, полученных на предыдущем этапе распознавания. Ошибка отклонения вычисляется как среднее значение относительной ошибки длительностей принятого символа и ожидаемого. Вычисленная ошибка отклонения сравнивается с заданным порогом и по результату сравнения принимается решение о соответствии принятого сигнала коду Морзе.

Поскольку длительности элементов кода Морзе меняются в процессе передачи, то при каждом положительном приеме кода Морзе значение символа «точка» обновляются. Тем самым, обеспечивается подстройка к параметрам входного сигнала.

На рис. 5 представлены зависимости вероятностей ошибочного решения для гипотез H1 и H2 по результатам моделирования оптимального и квазиоптимального алгоритмов. По результатам моделирования оптимального алгоритма построены сплошной линией зависимость вероятности ошибочного решения для гипотезы H1 , пунктирной – для гипотезы H2 . Так же на этом графике по результатам моделирования квазиоп- тимального алгоритма представлены зависимости вероятностей ошибочного решения для гипотез H1 и H2 (треугольниками и квадратами).

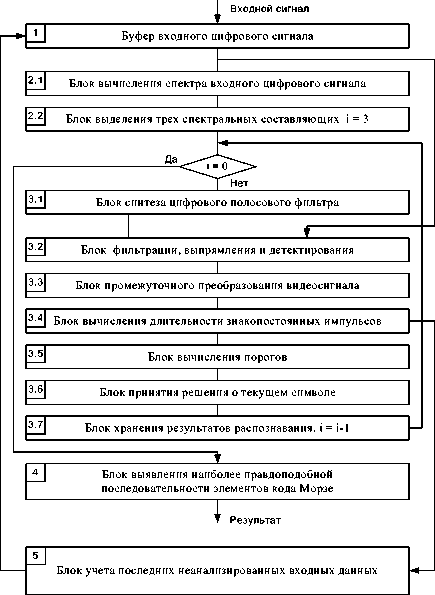
Рис. 4. Квазиоптимальный алгоритм различения элементов кода Морзе

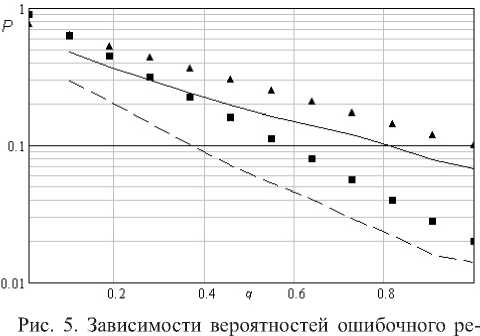
шения от уровня полезного сигнала для гипотезы H ₁ и H ₂

Рассмотренное решение задачи различения сигналов оптимально, если точно известна длительность τ0 импульсного сигнала. Однако, как правило, τ0 задается диапазоном значений (т0min,т0max). Соответственно и при гипотезе H2 длительность информационного сигнала «тире» может лежать в диапазоне ( 3 т0min ,3т0max). В этом случае возможны два подхода к решению задачи: оценка τ0 по наблюдениям и подстановка в решающее правило или применение решающего правила для различения сложных гипотез H1, H2. Воспользуемся вторым подходом.

Процедура обнаружения-различения сложных гипотез будет состоять из следующих этапов. Вначале осуществляется проверка гипотезы H ₀ при альтернативе H ₁ или H ₂ на интервале τ ₀ . В случае отклонения гипотезы H 0 осуществляется оценивание длительности сигнала τ по методу максимального правдоподобия. Полученная оценка Т сравнивается с серединами интервалов τ ₀ и 3τ ₀ . Если τ ближе к τ ₀ , то выбирается гипотеза H ₁ , в противном случае – H ₂ .

В предложенном алгоритме необходимо найти оценку Т по методу максимального правдоподобия. Для этого запишем функцию правдоподобия

T

- — ( U ( t ) - U ( t ,т) ) 2 dt

Ю(U(t)/т) = Koe N00            , где U(t,T) = U0 cosoj, 0 < t < т; т < T; T - интервал наблюдения. Максимуму функции соответствует минимум выражения

T

— J( U ( t ) - U ( t , T ) ) dt N _{0 0}

или максимум

L ( t ) =

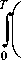
U ( t ) -1 U ( t , t )| U ( t , t ) dt.

Поскольку в рассматриваемом случае прямоугольного сигнала не существует производной dL(T)/dT, то оптимальная оценка T должна находиться непосредственно на основе максимизации L(t). Процесс поиска такой оценки иллюстрируется на рис. 6. При изменении параметра τ математическое ожидание функции L(t) линейно растет и достигает максимума при т = ти. После этого M {L(T)} уменьшает -ся. На рис. 6 показаны характерные значения M {L(t)} . С учетом помех максимум L(t) будет зафиксирован в точке T, отличающейся от ти на величину случайной ошибки £ = Т - ти. Для нахождения дисперсии этой ошибки и, следовательно, рабочих характеристик алгоритма различения сигналов можно воспользоваться неравенством Рао-Крамера. Как известно, минимально достижимая дисперсия ошибки оце- нивания, соответствующая методу максималь- ного правдоподобия, находится по формуле

Т(Т )^,

σ ε ²

где

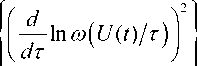
инфор-

мация относительно т, содержащаяся в U ( t ) , 0 ≤t≤T (по Фишеру).

В нашем случае

( 2

I ^{( т} ) = M 11 — J( U ^{( t} ) - U ^{( t , т} ) )

_⎪⎩⎝ N _{0 0}

dU ( t , t ) dt

∂ τ

4 г г

= M1 172 f Jn ⁽ t' ^{) n ( t} 2 )

1 v n n

0 00

dU ( t 1 , t ) dU ( t 2 , t )

∂ τ ∂ τ

dt ₁ dt ₂ ⎬ =

На рис. 7 приведены зависимости дисперсии ошибки оценивания длительности, полученные по формуле (5) и на основе нахождения оценки длительности импульса по методу максимального правдоподобия. На графике сплошной линией показана дисперсия ошибки оценивания длительности символа «точка», пунктирной – символа «тире»; кругами и треугольниками – практические зависимости дисперсии ошибки оценивания длительности символа «точка» и «тире», соответственно.

jfs v c t z T ) Y dt , ₀ ^∫ ₀ ⎝∂ τ    ⎠

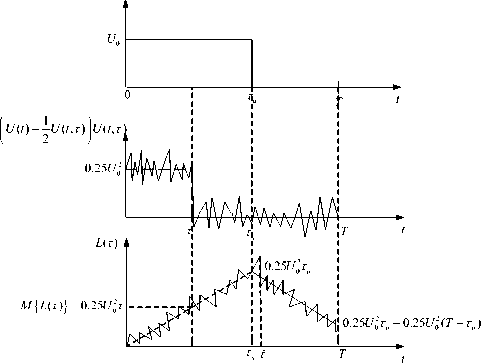
Рис. 6. Процесс оптимального оценивания длительности сигнала

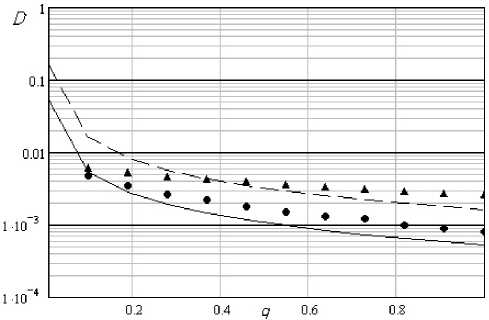
Рис. 7. Дисперсия ошибки оценивания длительности импульса

где U(t, T ) = U 0 V(t, T )cos ^ 0 t ; V ( t , т ) - функция, определяющая форму импульса. При заданной форме импульса полученные соотношения позволяют найти минимальную дисперсию ошибки оценивания и характеристики различе- _-t ²

ния сигналов. Например, если V ( t ,т) = e ^т 2 , то dV/5т = 2 t ² e ^т 2 /т ³ и количество информации по Фишеру

Найденные оптимальные алгоритмы различения импульсных сигналов определяют потенциальную помехоустойчивость приема сигналов с полностью известными параметрами, а также для случая, когда неточно известна длительность сигнала. В более реалистичном случае принимаемых сигналов является случайной начальная фаза Ф ( t ). Для нахождения оптимальных алгоритмов различения сигналов необходимо проинтегрировать апостериорные вероятности и с учетом равномерного распределения го ( ф ) = 1/2 п , - п <  ф <  п . Для гипотезы H ₁ получим

I (т ) =

2 U 02 7 4 t 4 e

N 0 τ ^∫ 0 τ ⁶

∞ где C = ∫ z ⁴ e ^-2z dz. 0

_-2t ²

Таким

7 dt = ⁸UL C , ^N 0 ^τ

образом, относитель-

ная дисперсия ошибки оценивания длительности колоколообразного сигнала

σ ε² τ ²

⎛ 8U 0² τ _C⎞ ^-1 ₌1

^⎜⎝N 0      ^⎟⎠     8CS ^,

где S – отношение сигнал/шум.

Л1(,) = Px (U (t), 0 < t < T, Фм Po (U (t), 0 < t < T) =

τ ₀

2 ^T °_r                               E

= exp ^Tj U(t)U0 c°s(®ot + Ф)dt - 7Г ,

V N 0 0                         N o J

где E ₁ = U ₀ ² τ ₀ 4 – энергия сигнала «точка». После интегрирования получим отношение правдоподобия в виде

n                     - Ei   Л 2z л1 = J to(Ф)Л1 (Ф)dФ = e N0 I0 —

-π                          ⎝^N 0 ⎠

где       Z = -JZ 2 + Z 22 ;     Z 1 = U 0 J U ( t ) cos ₀ tdt ;

τ ₀

Z2 = U0 JU(t)sin ^0tdt;   I0 (•) — модифициро- ванная функция Бесселя нулевого порядка. Точно так же усредненное по фазе отношение правдоподобия

3E 1

Λ 2

( ^1

⎜_{⎝N 0} ⎟_⎠

3 τ ₀

где Y = 7 V.' + Y 22 ; YY = U 0 J U ( t ) cos ^ 0 tdt;

3τ ₀

Y 2 = U 0 J U ( t )sin a ₀ tdt .

Оптимальное правило различения сигналов со случайной фазой можно сформулировать следующим образом. Для принятия решения необходимо сравнить между собой 3 числа «1» , Λ ₁ и Λ ₂ и выбрать большее из них. Если большим числом окажется единица, то принимается гипотеза H ₀ ; если Λ ₁ , то H ₁ ; а если же Λ ₂ , то H ₂ . После логарифмирования отношения правдоподобия правило сводится к сравнению нуля и следующих величин

λ ₁ =ln Λ ₁ =ln I ₀

⎛ 2Z ⎞E ₁

-

^⎜⎝^N 0 ^⎟⎠^N 0

λ ₂ =ln Λ ₂ =ln I ₀

⎛ 2Y ⎞3E ₁

-

^⎜⎝N 0 ^⎟⎠N 0

Техническая реализация правила различения может быть осуществлена как с помощью корреляторов, так и с помощью согласованных фильтров. В первом случае после нахождения корреляционных интегралов с квадратурными компонентами U ( t )cos rn ₀ t и U ( t )sin ® ₀ t входного сигнала вычисляются статистики Z и Y . После этого необходимо выполнить нелинейное преобразование вида In I₀ ( • ) . Выполняя вычитание половины относительной энергии ожидаемого сигнала, получаем логарифмы отношений правдоподобия λ ₁ и λ ₂ , которые сравниваются между собой и со значением ноль в решающем устройстве.

Согласованные фильтры СФ1 и СФ2 соответствуют сигналам «точка» и «тире», а временное селектирование должно осуществляться в моменты, когда напряжение на выходах согласованных фильтров соответствует заднему фронту каждого из сигналов.

Вероятностные характеристики найденного оптимального алгоритма различения сигналов могут быть найдены по той же схеме, что и для когерентного приема. Наконец, точно так же может быть решена задача различения сигналов, если их длительности известны не точно. Тогда нужно найти максимум функции правдоподобия, усредненной с учетом равномерного распределения длительности сигнала.

Заключение

Рассмотрены оптимальные и квазиопти-мальные алгоритмы различения импульсных тональных сигналов кода Морзе при полностью известных параметрах сигналов, а также при неточно известной длительности сигналов и при наличии случайной фазы сигналов. Проигрыш вероятности правильного решения квазиоптимального алгоритма по отношению к оптимальному составляет порядка 40-50%.