Оптимальные вибрационные поля в задачах моделирования динамических состояний технических объектов
Автор: Елисеев А.В., Кузнецов Н.К.
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Механика
Статья в выпуске: 1 т.24, 2024 года.
Бесплатный доступ
Введение. Управление вибрационными взаимодействиями актуально в производственных процессах, связанных с жидкими и сыпучими средами, системами твердых тел, испытывающих кинематические или силовые возмущения. При этом нет единой методологической основы для формирования вибрационных взаимодействий. Не решены вопросы построения оптимальных вибрационных полей технических объектов. Цель исследования - развитие структурного подхода к разработке математических моделей в задачах формирования, оценки и коррекции вибрационных полей технических объектов в условиях интенсивных силовых и кинематических нагружений. Ставится задача построения вибрационных полей, оптимальных по совокупности требований, с возможностью выбора критерия оптимальности вибрационного поля технического объекта.Материалы и методы. В качестве базовой методологии применяется структурный подход. Он основан на сопоставлении механических колебательных систем, используемых как расчетные схемы технических объектов, и структурных схем систем автоматического управления, эквивалентных в динамическом отношении. Для структурного математического моделирования использовали формализм Лагранжа, элементы операционного исчисления на основе интегральных преобразований Лапласа, разделы теорий колебаний, алгебраические методы, теорию сплайн-функций.Результаты исследования. Предложен подход к выбору критериев оптимальности вибрационных полей на основе минимизации невязки вибрационных полей для различных необходимых условий. Проблема рассматривается в рамках механической колебательной системы, образованной твердыми телами. Показано, что оптимальное вибрационное поле определяется внешним возмущением и должно удовлетворять условию Ay̅ = b. Здесь A - матрица, отображающая оператор условий на форму вибрационного поля в контрольных точках; b - вектор значений характеристик вибрационного поля; «-» над y означает амплитуду колебания установившейся компоненты координаты. Для оценки поля с учетом зашумленных или недостоверных требований к динамическим характеристикам используется параметр сглаживания, обозначающий приоритет критерия оптимальности формы вибрационного поля. Построение поля для механической колебательной системы показало, что значение амплитуд колебания обобщенных координат сохраняется постоянным при изменении частоты внешних кинематических возмущений. Рассмотрены два подхода к коррекции критериев оптимальности поля: уравнивание амплитуд колебаний координат технического объекта и выбор энергетического оператора.Обсуждение и заключение. Развитие прикладной теории оптимальных вибрационных полей предполагает, во-первых, сопоставление оператора энергии и оператора требований к форме вибрационного поля в теории абстрактных сплайнов. Вторая пара сопоставляемых элементов - критерий оптимальности вибрационного поля и система требований к характеристикам поля в контрольных точках. Усовершенствованная таким образом структурная теория оптимальных вибрационных полей найдет применение в разных отраслях. Точные расчеты в формировании, оценке и коррекции состояний систем при вибрационном нагружении необходимы в задачах повышения долговечности конструкций, улучшения измерений в сложных колебательных системах, разработки новых технологий и материалов
Структурное математическое моделирование, механические колебательные системы, оптимальное вибрационное поле, минимизация невязки вибрационных полей
Короткий адрес: https://sciup.org/142240670
IDR: 142240670 | УДК: 629.4.015, | DOI: 10.23947/2687-1653-2024-24-1-7-22
Текст научной статьи Оптимальные вибрационные поля в задачах моделирования динамических состояний технических объектов
Research article
Optimal Vibration Fields in Problems of Modeling Dynamic States of Technical Objects Andrey V. Eliseev1,2 ©И, Nikolai K. Kuznetsov2 Ф
-
1 Irkutsk State Railway Transport Engineering University, Irkutsk, Russian Federation
-
2 Irkutsk National Research Technical University, Irkutsk, Russian Federation
Introduction. Vibration interaction control is timely in production processes related to liquid and bulk media, systems of solids experiencing kinematic or force disturbances. At the same time, there is no single methodological basis for the formation of vibrational interactions. The issues of constructing optimal vibration fields of technical objects have not been addressed. The objective of the study is to develop a structural approach to the development of mathematical models in the problems of formation, evaluation, and correction of vibration fields of technical objects under conditions of intense force and kinematic loads. The task is to build vibration fields that are optimal in terms of the set of requirements, with the possibility of selecting the criterion of optimality of the vibration field of a technical object.
Materials and Methods . A structural approach was used as the basic methodology. It was based on a comparison of mechanical vibratory systems used as computational schemes of technical objects, and structural schemes of automatic control systems, which are equivalent in dynamic terms. Lagrange formalism, elements of operational calculus based on Laplace integral transformations, sections of vibration theories, algebraic methods, and the theory of spline functions were used for structural mathematical modeling.
Results. An approach to the selection of criteria for the optimality of vibration fields based on minimizing the residual of vibration fields for various required conditions was proposed. The problem was considered within the framework of a mechanical vibratory system formed by solids. It was shown that the optimal vibration field was determined by an external disturbance and was to satisfy condition Ay̅ = b . There, A — matrix mapping the operator of conditions to the shape of the vibration field at control points; b — vector of values of vibration field characteristics; “–” above y meant the vibration amplitude of the steady-state component of the coordinate. To evaluate the field with account for noisy or unreliable requirements for dynamic characteristics, the smoothing parameter was used, indicating the priority of the criterion of optimality of the vibration field shape. The construction of a field for a mechanical vibratory system showed that the value of the vibration amplitudes of generalized coordinates remained constant when the frequency of external kinematic disturbances changed. Two approaches to the correction of the field optimality criteria were considered: equalization of the vibration amplitudes of the coordinates of a technical object and the selection of an energy operator.
Discussion and Conclusion. The development of the applied theory of optimal vibration fields involved, firstly, the correlation of the energy operator and the operator of the requirements for the shape of the vibration field in the theory of abstract splines. The second pair of comparable elements was the criterion of optimality of the vibration field and a system of requirements for the characteristics of the field at control points. The structural theory of optimal vibration fields improved in this way will find application in various industries. Accurate calculations in the formation, assessment, and correction of the states of systems under vibration loading are required in the tasks of increasing the durability of structures, improving measurements in complex vibratory systems, and developing new technologies and materials.
Введение. Особенности вибрационных взаимодействий учитываются при создании производственных технологий [1] . Использование вибрационных методов интенсификации технологических процессов требует развития математического моделирования динамических состояний технических объектов в условиях вибрационного нагружения. В научной и прикладной литературе прорабатываются вопросы, связанные с теорией колебаний и автоматического управления, теоретической механикой и динамикой машин [2] . В частности, в динамике машин особенности вибрационных взаимодействий учитываются в двух типах задач. Первый: задачи виброизоляции и виброзащиты [3] . Второй: задачи, связанные с оценкой, формированием и коррекцией состояний технических объектов в условиях интенсивных силовых или кинематических нагружений [4] . В последнем случае обращают на себя внимание эффекты вибрационных взаимодействий, которые находят применение в таких технологических процессах, как:
-
- транспортировка горных пород;
-
- разделение сыпучих материалов на фракции;
-
- упрочнение поверхностей длинномерных элементов авиационных конструкций;
-
- пространственная ориентация деталей в процессе сборки.
Задачи виброзащиты связаны с решением проблем безопасности железнодорожного транспорта. Речь идет, в частности, о вопросах динамического состояния элементов подвески [5] , шуме и вибрации [6] . Задачи оценки динамических состояний, вызванных значительными нагрузками, возникают при оценке вибрационных характеристик рельсового пути с композитными шпалами [7] . Требуют контроля вредные колебания, распространяющиеся в городской среде от движущегося состава, и а этом случае тоже необходима оценка сложных динамических состояний [8] . Аналогичные примеры связаны с отслеживанием взаимодействий тележки вагона с рельсами [9] . Динамическое состояние формируется при нарушении скользящего контакта головки пантографа с контактным проводом [10] . В данном контексте следует упомянуть и задачи анализа реакции рельса на вертикальные воздействия со стороны движущегося транспортного средства [11] .
Еще одна обширная группа задач, требующих оценки динамических состояний элементов, — вибрационные процессы технологических машин [12] . Так, динамическое состояние машин вибрационного грохочения зависит от формирования динамических состояний нескольких корпусов, которые можно рассматривать как твердые тела с учетом характера упругих связей между ними [13] . Существенный фактор, определяющий динамические состояния объектов технологического назначения, — частота колебаний [14] . Отдельно необходимо упомянуть вибрационные транспортные машины, динамическое состояние которых определяет особенности движений [15] .
Стоит отметить результат обобщения задач оценки, формирования и коррекции динамических состояний технических объектов в условиях интенсивных нагружений. Данный подход открыл возможность уточнить представления о том, как распределения амплитуд колебаний координат контрольных точек зависят от связности внешних возмущений.
Параметры внешних вибрационных возмущений определяют возможности реализации динамических эффектов, которые могут действовать разнонаправленно:
-
- представлять опасность для функционирования технических объектов;
-
- повышать производительность технологических процессов.
Пример негативного эффекта — превышение допустимых значений амплитуд колебаний. Полезные эффекты: существенное уменьшение амплитуд колебаний координат и установление определенного распределения амплитуд.
В задачах вибрационного упрочнения длинномерных деталей под динамическими эффектами можно понимать совпадение форм колебаний контрольных точек рабочих органов вибрационных технологических машин. Это обеспечивает одномерность и однородность вибрационного поля, что согласуется с требованиями к динамическому качеству взаимодействий рабочей среды и поверхности упрочняемой детали. Необходимую форму движения рабочего органа можно выразить с помощью условий равенства амплитуд колебаний контрольных точек. Для исследования понятия вибрационного поля обобщается понятие динамического состояния в точке — одновременно рассматривается совокупность точек, распределенных по некоторому многообразию точек твердого тела или системы твердых тел [16] .
В задачах вибрационных взаимодействий можно отобразить ряд динамических эффектов с помощью рычажных, упругих, межпарциальных неудерживающих связей. Все они — факторы специфических динамических эффектов, которые проявляются под воздействием внешних возмущений особенной конфигурации. Для определения таких конфигураций внешних возмущений, обеспечивающих динамические эффекты, предполагается разработка методологической базы, позволяющей строить математические модели вибрационных полей с учетом системы требований к особенностям взаимодействий элементов системы.
Механика
Предполагаемая методологическая база должна обладать:
-
- эффективным математическим аппаратом;
-
- инструментом наглядного отображения структурных особенностей;
-
- возможностями построения динамических аналогий для обобщения разработанных методов на широкий класс физических процессов.
Материалы и методы. Методологической базой может служить структурный подход, основанный на сопоставлении механических колебательных систем и систем автоматического управления [17] . В этом случае механическая колебательная система рассматривается как расчетная схема технического объекта. Ее сопоставляют со структурной схемой эквивалентной в динамическом отношении системы автоматического управления. Установленное соответствие позволяет анализировать и оценивать динамические характеристики технических объектов с учетом представлений об установившихся формах колебаний механической системы на основе аппарата теории автоматического управления [18] . У технологии структурного математического моделирования есть особенности, связанные с оценкой динамических состояний. Для нее используют передаточные функции структурных схем. Входные сигналы для названных функций — внешние возмущения, выходные — колебания координат оцениваемого объекта. Каждую координату системы можно соотнести с показателем амплитуды установившегося колебания. Это позволяет рассматривать распределение амплитуд по точкам системы как вибрационное поле технического объекта. Построение вибрационного поля с учетом ряда требований относится к классу обратных задач динамики, которые в общем случае могут быть некорректными. Один из методов решения некорректных задач связан с регуляризацией исходной задачи путем введения критериев оптимальности.
Перечисленные особенности оценки динамических состояний технических объектов указывают на необходимость разработки общего подхода в методологии построения вибрационных полей с учетом критериев оптимальности. Вместе с тем методология формирования, оценки и коррекции вибрационных полей с заданными характеристиками недостаточно детализирована. В частности, не предусмотрена возможность строить вибрационные поля по критериям оптимальности.
Представленная работа посвящена развитию методологии структурного математического моделирования. Для этого решается класс частных задач построения вибрационных полей технических объектов с условиями по амплитудам колебаний, которые отображают требования к динамическим эффектам и учитывают критерии оптимальности.
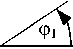
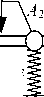
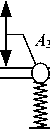
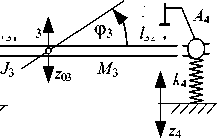
Основные положения. Постановка задачи. Рассматривается модельная механическая колебательная система, образованная совокупностью твердых тел в условиях вибрационного нагружения кинематической природы. Модельная система (рис. 1) имеет 5 степеней свободы, состоит из 4 звеньев в виде твердотельных стержней с массами M i , моментами инерции J i , центрами тяжести в точке O i , отстоящих от крайних точек А i и А i+ 1 на расстояния l 1 i и l 2 i , где i = 1 … 4.
Твердые тела в виде стержней сочленены между собой в крайних точках — это места крепления упругих элементов, установленных на опорных поверхностях, совершающих синфазные гармонические колебания (рис. 1).
л y1
▼l
А k1
/////
▼ z 1
O 1
y 2
l 12
z 01 M 1
l 21 O 2
J 2
k 2
z 2

y 2 l 22
z 02 M 2
k 3
z 3
y 4
l 32 т
l 31 O 3
k 4
l 41 O 4
J 4
y 5
l 42 ♦
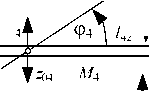
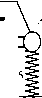
▼ z 5
Рис. 1. Механическая колебательная система, образованная твердыми телами A 1 A 2 , A 2 A 3 , A 3 A 4 , A 4 A 5 :
A — точки сочленения твердых тел; О i — центры тяжести; z i — опорные поверхности; J i — моменты инерции
Под воздействием внешних кинематических возмущений z i со стороны опорных поверхностей система совершает малые установившиеся колебания относительно положения статического равновесия. Внешние кинематические возмущения представляют собой связные синфазные колебания:
z i = z g γ i . (1)
Здесь z g — гармоническое возмущение вида Asin (ω t ), где ω — частота и γ i — коэффициенты связности внешних возмущений; i = 1 … 5 . В общем случае коэффициенты связности (1) — это внешние возмущения определенной структуры.
Необходимые динамические эффекты обеспечиваются совокупностью модельных условий, а именно: амплитуды колебаний координат контрольных точек технического объекта принимают фиксированные значения вне зависимости от частоты внешних возмущений.
Задача — определить для механической колебательной системы такие внешние кинематические возмущения, чтобы соответствующее вибрационное поле в контрольных точках удовлетворяло заданной совокупности условий в виде фиксированных амплитуд колебаний.
Результаты исследования
Математическая модель. Для составления системы дифференциальных уравнений рассматриваются координаты {у 1 , у 2 , у 3 , у 4 , у 5 } смещений точки A i , i = 1...5 относительно положений статического равновесия. Наравне с координатами { y 1 , y 2 , y 3 , y 4 , y 5 } рассматриваются:
-
- координаты { z 01 , z 02 , z 03 , z 04 , z 05 }, отображающие смещения центров тяжести O i стержней относительно положений статического равновесия;
- координаты {ф 1 , ф2, ф3, ф4, ф5} малых углов поворота вокруг центров тяжести. Координаты z 0 i , ф i , yi связаны между собой выражениями:
| z о i = a i y i + b i у1 +i {ф i = С (У i +1 - У i ) ’
l i 2 l i 1 1
здесь at =-------,b =-------, Ci =------ li1 + li2 U + li 2 li1 + li2
Математическая модель в виде дифференциальных уравнений Лагранжа 2-го рода строится на основе выражений для потенциальной и кинематической энергии. Их можно представить в матричном виде с помощью скалярного произведения Q векторов в R n :
п = 2 (к(у - z ),(y - z) , т = 2 (мо0 , —0) + 2 J Ф , Ф },
1 • z z
1 • z z
здесь z о , ф — производные координат z о , ф .
( kI
K =
k 2
I 0
M 3 „
M 4 J
(ф1 ^
—z
ф =
Ф 2
Ф 3
1Ф4 J
, z 0 =
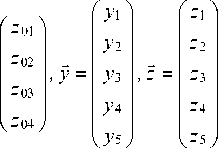
.
Векторы — о e R 4, Ф e R 4,
у e R5 с учетом (2) связаны между собой соотношениями:
( a 1
Здесь U =
a 2
b 3
,V =
z o = Uy, ф = V.
a 4
b 4
c1
- c 2
- С 3
- c 4
В координатах {yi } кинетическая энергия (3) принимает вид:
т = 1 (( U T MU + V T JV ) у ,y.
С учетом выражений (2)-(5) уравнения Лагранжа 2-го рода принимают вид: ( U T MU + V T JV ) у + Ку = К — .
Предполагается, что начальные условия — нулевые. В этом случае интегральные преобразования Лапласа приводят (6) к системе алгебраических уравнений:
( M 0 p 2 + K ) у = Kz , (7)
где M 0 = U T MU + V T JV — матрица системы, знак «-» над векторами у и z обозначает преображение по Лапласу [19] .
Механика
С помощью методов [18] алгебраическую систему (7) можно представить в виде структурной схемы эквивалентной в динамическом отношении системы автоматического управления (рис. 2).
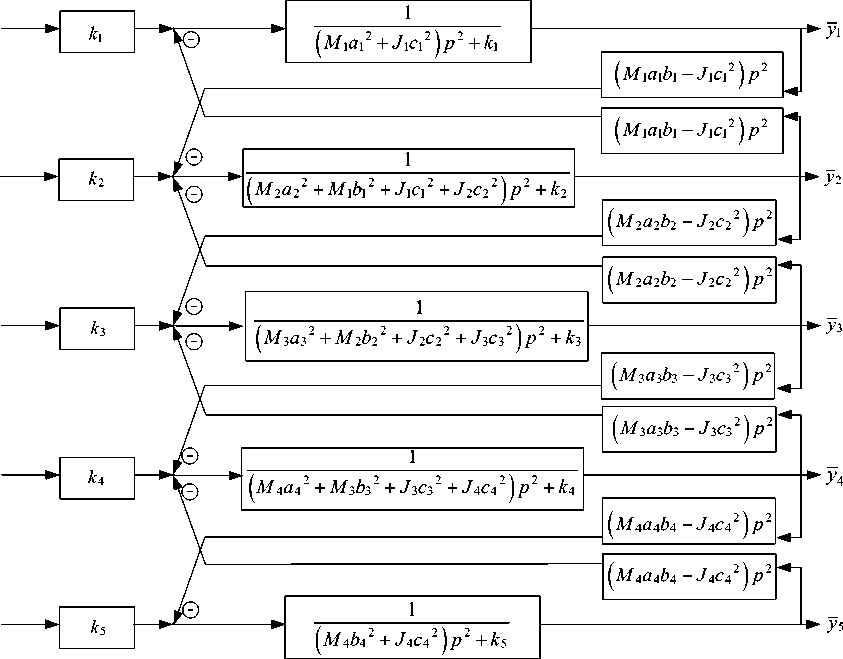
Рис. 2. Структурная схема механической колебательной системы (рис. 1): p = j Ю , j = -- 1
На основе структурной схемы для фиксированного набора коэффициентов связности у i можно построить передаточные функции. Они определяются выбором объекта, динамическое состояние которого оценивается по выражениям:
W 1 (p) = I4 W 2 (p) = y 2 W 3 (p) = y 3 W 4 (p) = y 4 ,W 5 (p) = y 5 . (8) z g z g z g z g z g
Амплитудно-частотные характеристики передаточных функций (8) в физическом смысле рассмотрим как рычажные связи, представляющие собой отношения амплитуд колебаний координат { y i } к амплитуде колебаний внешнего кинематического возмущения { z g }.
В рамках рычажной интерпретации положительные ветви амплитудно-частотной характеристики отображают рычажные связи 1-го рода (реализуются двуплечими рычагами). Отрицательные ветви отображают рычажные связи 2-го рода (реализуются двуплечими рычагами). Режимы резонанса и динамического гашения колебаний отображают вырожденные рычажные связи, которые можно представить условными виртуальными рычагами с нулевыми или бесконечными плечами.
Выбор структуры внешних кинематических возмущений путем задания коэффициентов связности { Y i } однозначно определяет амплитуды колебаний координат системы. Вместе с тем требования, предъявленные к амплитудам колебаний, могут:
-
- предполагать неоднозначность решения;
-
- прямо противоречить друг другу;
-
- допускать лишь частичное соблюдение из-за больших погрешностей.
В таких ситуациях необходимы критерии выбора внешних возмущений, которые однозначно определят вибрационное поле по совокупности требований. Логичный для этой задачи подход основан на том, что внешние кинематические возмущения, обеспечивающие необходимые условия, можно определить по критерию оптимальности вибрационных полей. Суть данного критерия: амплитуды колебаний технического объекта подбираются таким образом, что доставляют минимум определенному энергетическому функционалу [20] .
Формирование вибрационных полей механических колебательных систем на основе критерия оптимальности. В рамках модельной задачи предполагается, что в точках A i 1 , A i 2... A ik вибрационного поля {yi }, i = 1. n механической колебательной системы задано определенное условие. Оно заключается в том, что амплитуды {yik }, к = 1. m принимают фиксированные значения { y 01. y 0 m }:
У А = у 0 к. (9)
Здесь к = 1... m , где m отображает количество точек, в которых заданы условия на амплитуды. В этом случае и далее по тексту знак «-» над у или z означает амплитуду колебания установившейся компоненты координаты, если не оговорено иное. В остальных точках {y i , i = 1. n}/{yik , к = 1. m } не заданы требования к значениям вибрационного поля.
Необходимые требования (9) можно представить в виде:
Ay = b, (10)
где A — матрица, отображающая оператор условий на форму вибрационного поля в контрольных точках; b — вектор значений характеристик вибрационного поля [20] .
В общем случае условия для вибрационного поля (10) могут быть неопределенными или несовместными. Для рационального учета несовместных или неопределенных требований к вибрационному полю вводится критерий его оптимальности и допущение, что совокупность требований может быть выполнена с некоторым приближением.
Под значениями у 1 , у 2... уп понимаются амплитуды колебаний установившихся компонент, поэтому для каждой фиксированной частоты ю внешних возмущений z можно поставить вариационную задачу построения оптимального вибрационного поля, которое:
-
- доставляет минимум энергетическому функционалу;
-
- отображает представления о формах колебания или о значениях потенциальной или кинетической энергии.
В общем случае энергетический функционал определяет особенности распределения амплитуд динамических характеристик по точкам механической колебательной системы.
В рамках рассматриваемой модельной задачи энергетический функционал, заданный оператором T e , отображает неравномерность вибрационного поля. Ее показатель — сумма квадратов разностей отклонений амплитуд колебаний соседних точек:
n -1
T e (У) = ^ (У +1 — У) 2 . (11)
i =1
Нулевое значение энергетического функционала (11) определяет равномерное вибрационное поле, амплитуды колебаний точек которого равны между собой. Минимизация энергетического функционала с учетом заданных условий на амплитуды колебаний в контрольных точках (10) определяет форму вибрационного поля, экстремально близкую к равномерной.
Примем во внимание ряд условий:
-
- фиксированная частота внешних возмущений ю;
-
- вибрационное поле оптимально в смысле критерия, заданного энергетическим функционалом;
-
- амплитуды вибрационного поля в контрольных точках удовлетворяют условиям (10).
В этом случае формальную постановку задачи построения вибрационного поля можно представить в виде:
у а ( ю ) = arg min T e (у) , (12)
Ay=b,y=(-M 0Ю2 + K) Kz где у — вибрационное поле, заданное внешними кинематическими возмущениями z , которые рассматриваются как независимые вариационные параметры.
Для фиксированной частоты ω вибрационное поле y σ (ω), точно удовлетворяющее совокупности требований, формально находится как решение (12) условной минимизации квадратичной функции (11) с учетом линейных условий (10):
L(y, Л ) = (Т е 0 у,у) + A4y - b, ^ ^ min i . (13)
Л,у = ( M 0 p 2+ K ) Kz
Здесь у — вибрационное поле, определяемое внешним кинематическим возмущением; Л = (Х 1 .Х m ) — коэффициенты Лагранжа. Минимизация в задаче (13) идет по параметрам z внешних возмущений. Для фиксированных значений z амплитуд внешних возмущений создаваемое вибрационное поле у является решением задачи:
Механика
( - M 0 Ю 2 + K ) у = Kz , (14)
где M 0 = U T MU + V T JV — матрица системы.
Вибрационное поле y , точно удовлетворяющее заданным значениям (10), можно определить на основе решения задачи условного минимума с помощью функции Лагранжа:
L(z, A ) = / те о ( M о p 2 + K ) Kz, ( M о p 2 + K ) Kz\ + A a ( M о p 2 + K ) Kz - Ь, Л ^ min , (15)
где z — вектор амплитуд колебаний внешних кинематических возмущений; T e 0 — матрица, определяющая квадратичную форму энергетического функционала (11).
Внешние возмущения Zя, формирующие необходимое вибрационное поле, множители Лагранжа Л находятся решением системы:
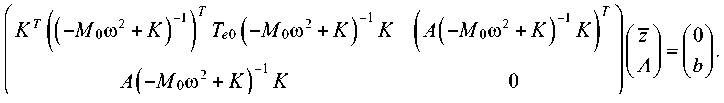
z 1-1 0 л Н ь
A ( - M 0 Ю 2 + K ) K
Итак, z σ — это решение задачи условной минимизации (15), (16). Оптимальное вибрационное поле y σ определяется внешним возмущением z σ и имеет вид:
y „ = ( - M о ro 2 + K )- 1 Kz a .
Здесь y σ можно назвать интерполирующим вибрационным полем, так как при условии совместности (16), оно точно удовлетворяет требованиям (10). С учетом зависимости от частоты ω, совместность и определенность системы (16) характеризуется в рамках теорем существования и единственности решений систем уравнений теории сплайнов [20] . При условии совместности и определенности системы (16) и (17), оптимальное вибрационное поле y σ точно удовлетворяет совокупности условий (10).
Необходимые условия (10) могут содержать зашумления, ошибки или быть противоречивыми. С учетом противоречивых или недостоверных требований, вибрационное поле можно построить с помощью решения задачи сглаживания. Ее результат — оптимальное вибрационное поле, удовлетворяющее условиям, отличным от исходных требований, но близких к ним.
Оценка вибрационного поля с учетом зашумленных или недостоверных требований к динамическим характеристикам. Вибрационное поле y σ (ω) (17), удовлетворяющее условиям (10), может быть аппроксимировано с помощью вибрационного поля y α (ω) с учетом недостоверности или противоречивости необходимых требований (10):
m
y a ( ro) = arg min y=(-M ого2 + K)
a T e ( y) + ^ ( y , k - y о k ) 2
Здесь T e y — оператор, отображающий критерий оптимальности формы вибрационного поля; α — параметр сглаживания, обозначающий приоритет критерия оптимальности формы вибрационного поля по отношению к требованиям выполнения условий (10).
В выражении (18) z рассматривается как независимая переменная. Вибрационное поле y α (ω) можно назвать сглаживающим, так как оно приближенно удовлетворяет системе необходимых требований.
Вибрационное поле y α определяется системой уравнений, полученной путем минимизации функции Лагранжа:
L a (y( z)) = a (Т о о y,y) + || Ay - b |2 ^ min.
z
Здесь y ( z ) является вибрационным полем, формируемым внешним кинематическим возмущением z :
( - M о го 2 + K ) y = Kz. (2о)
Сделаем замену на основе (20):
y = ( - M о го 2 + K ) Kz.
Теперь функция Лагранжа (19) с учетом (20) и (21) приводится к виду:
где
ylAy— — длина вектора в Rn , выраженная через скалярное произведение
_z - b ^ min , (22)
z
Рассмотрим внешние кинематические возмущения z а. Они формируют оптимальное вибрационное поле у а, которое сглаживает заданные условия (10) и является решением задачи минимизации (22). Такие возмущения определяются системой:
- 1 T1 - 1 - 1 TT
- M о ® 2 + K ) ) ( а Те 0 + A T A )( - M а ® 2 + K ) Kz а = K T ( ( - M о ® 2 + K ) ) A T b.
После упрощений системы (23) искомые амплитуды кинематических возмущений z а определяются выражением:
z а = K-1 (M 0 p2 + K )(а T0 + AT A )-1 AT b.(24)
Как показано выше, внешние возмущения z а (24) — это решение задачи (23) с учетом выбора параметра сглаживания а. Эти возмущения обеспечивают построение вибрационного поля у а, которое приблизительно удовлетворяет совокупности требований (10) с учетом возможной несовместности или недостоверности:
у а=( M 0 p2 + K )-1 Kz а.(25)
Вид вибрационного поля у а (25) явно не зависит от частот внешних возмущений ю:
уа=(а Те 0 + AT A )-1 AT b.(26)
Внешнее возмущение z α , обеспечивающее построение оптимального сглаживающего вибрационного поля у а (24), можно использовать для построения интерполяционного вибрационного поля у а по мере а^0. Выбор параметра сглаживания а определяется из условий малости невязки:
Ф( а) = ||Ay а- b| |2, где уа = (-Mо®2 + K) Kzа, zа — кинематическое возмущение (27).
Необходимо отметить, что вибрационное поле у а зависит от частоты ю неявно, через параметр сглаживания а = а(ю), выбор которого определяется частотой внешнего возмущения ю и значением невязки (27).
Построение вибрационного поля для механической колебательной системы. Вычислительный эксперимент. Пусть параметры механической колебательной системы (рис. 1) заданы жесткостями k i , массами Mi , моментами инерции J i и геометрическими характеристиками 1 1 i , 1 2 i (таблица 1).
Таблица 1
Параметры модельной механической колебательной системы
|
№ |
M , кг |
J , кг-м2 |
к , Н/м |
1 1 , м |
1 2 , м |
|
1 |
100 |
10 |
1000 |
1 |
1 |
|
2 |
200 |
20 |
2000 |
1 |
1 |
|
3 |
300 |
30 |
3000 |
1 |
1 |
|
4 |
400 |
40 |
4000 |
1 |
1 |
В качестве требований к амплитудам вибрационного поля заданы условия на значения в точках A i (таблица 2).
Таблица 2
Амплитуды колебаний в точках вибрационного поля (у , м)
|
Значения |
A 1 |
A 2 |
A 3 |
A 4 |
A 5 |
|
Необходимые |
0,002 |
- |
- |
- |
0,005 |
|
Сглаженные |
0,002 |
0,0027 |
0,0035 |
0,0043 |
0,005 |
В качестве энергетического функционала используется выражение (11), которое можно представить с помощью оператора Te:
T e
Су11
у 2
у 3
у 4
I у 5 J
^ у 2 - у 1
^
- у 2
y 4
- у 3
I у 5 - у 4 J
Г 1
- 1
- 1
- 1
-1у
( у11
у 2
у 3
у 4
I у 5 J
Механика
Выражение T e y ,T e y можно представить в виде:
TT e y,T e y) = (т/ T e y, y^ = ( T o 0 y, y} =

-1
-1
-1
-1
-1
-1
0 Pl y 2
y3
-I y 4
1 JI y 5 )
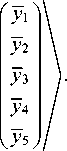
Здесь Te0 — матрица, определяющая квадратичную форму. Значение оператора Te y равно нулю на равномерном вибрационном поле y̅ = const. Амплитуды колебаний точек этого поля равны между собой для внешнего кинематического возмущения на произвольной частоте.
Зададим условия (10) на вибрационное поле. Для этого можно использовать оператор данных A 15 , который сопоставляет вибрационному полю y значения амплитуд в точках A 1 , A 5 :
A 15 :
( y 11
y 2
y 3
y 4
( 10 0
l 0 0 0
0 0 1
0 1 )
l У 5 )
p' 1
У 2
y 3
У 4
l У 5 )
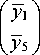
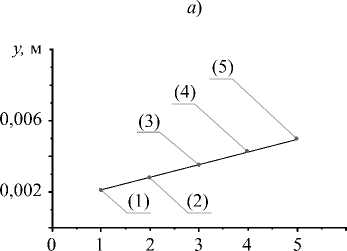
Вибрационное поле, интерполирующее заданные значения в точках A 1 , A 5 (таблица 2), можно аппроксимировать с помощью сглаживающего вибрационного поля у а для параметра сглаживания а = 0,01. Найдем разницу между значениями вибрационного поля и требуемыми значениями для выбранного коэффициента сглаживания α. Она определяется функцией невязки (27), значение которой составляет приблизительно 0,00001 м, где b = (0,002; 0,005) Т . Построенное вибрационное поле, сглаживающее интерполяционные условия, имеет линейную форму (таблица 2). Для фиксированного параметра сглаживания α = 0,01 совокупность амплитуд колебаний точек вибрационного поля y α , обеспечивающего близость к интерполируемым данным с невязкой φ(α) = 0,00001 м (таблица 2), имеет вид постоянных функций частоты внешнего возмущения ω (рис. 3 а ).
(4) (5)
О 2 4 6 го, рад/с
п, номер обобщенной координаты в )
м О -0,05
-0,015
б )
<р( со), м -
0,0003 ■
0,0001 ---------------------------------------------
0 2 4 6 го, рад/с
г )
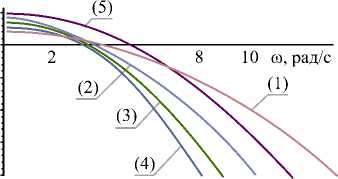
Рис. 3. Характеристики вибрационного поля: а — значения амплитуд колебаний сглаживающего вибрационного поля для частот внешних возмущений на интервале ω ∈ (0,100) рад/с; б — амплитуды внешних кинематических возмущений, обеспечивающие требуемые амплитуды колебаний в зависимости от частоты возмущений ω; в — форма вибрационного поля для частот на интервале ω ∈ (0...100); (1), (5) — требуемые значения вибрационного поля; (2), (3), (4) — значения, построенные на основе энергетического подхода; г — отклонение φ (ω) вибрационного поля от необходимых значений амплитуд в фиксированных точках технического объекта для постоянного коэффициента сглаживания α = 0,1
Значение амплитуд колебаний обобщенных координат в данном случае сохраняется постоянным при изменении частоты внешних кинематических возмущений z α . Эти возмущения, необходимые для обеспечения требуемых амплитуд в фиксированных точках вибрационного поля, существенно зависят от частоты ω внешних возмущений (рис. 3 б ).
Опишем вибрационное поле для фиксированной частоты или частотного интервала, на котором оно остается неизменным. Его можно представить графиком функции, зависящей от номера обобщенной координаты или координаты точки системы, в которой оценивается вибрационное поле. Форма вибрационного поля определяется критерием оптимальности. В частности, энергетический функционал T e 0 , определяющий критерий оптимальности, формирует линейную форму вибрационного поля (рис. 3 в ). Необходимо отметить, что «интерполяционное» вибрационное поле строится с помощью «сглаживающего» вибрационного поля, соответствующего параметру сглаживания α. Отклонение «сглаживающего» вибрационного поля должно быть незначительно. В рассматриваемом модельном примере для α = 0,1 величина отклонения сглаживающего вибрационного поля представляется константой φ (α) = 0,0001 м (рис. 3 г ). Необходимо отметить, что в общем случае энергетического функционала значение коэффициента сглаживания α, обеспечивающего фиксированный уровень невязки φ(α) = φ*, зависит от частоты ω и системы требований.
Таким образом, варианты формирования динамических состояний механических колебательных систем в виде вибрационного поля, удовлетворяющего системе условий, зависят от:
-
- энергетического функционала, отражающего особенности вибрационного поля;
-
- оператора, отображающего совокупность требований к вибрационному полю.
Возможны и другие варианты формирования вибрационного поля на основе выбора энергетического оператора.
Коррекция критериев оптимальности формообразования вибрационных полей с помощью весовых коэффициентов энергетических операторов. Выше рассмотрена форма вибрационного поля с возможностью уравнивания амплитуд колебаний координат технического объекта. Есть и другие подходы к минимизации амплитуд обобщенных координат, например, с помощью выбора энергетического оператора T E в виде тождественного отображения:
TE : y → Ey, где E — тождественный оператор.
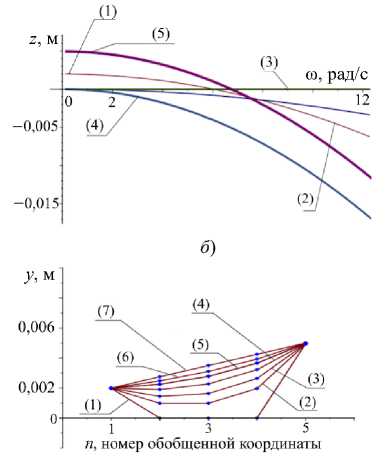
Формирование вибрационного поля на основе энергетического оператора Т Е связано с минимизацией или обнулением квадратичной функции амплитуд синфазных гармонических колебаний фиксированной частоты. В результате решения задачи сглаживания для энергетического функционала, соответствующего единичному оператору T E , формируется вибрационное поле. Амплитуды его колебания в точках A 2 , A 3 , A 4 равны нулю (рис. 4 а ), т. е. в точках A 2 , A 3 и A 4 реализуется режим динамического гашения колебаний.
г )
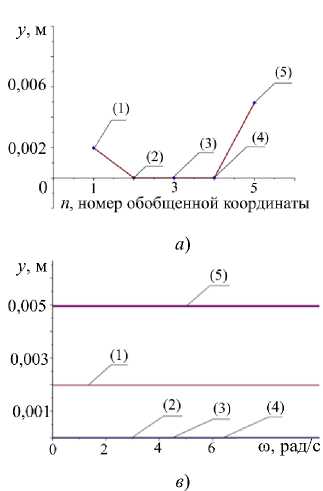
Рис. 4. Возможности коррекции вибрационного поля: а — форма вибрационного поля для энергетического функционала отображает минимально возможные амплитуды колебаний с учетом необходимых требований; б — амплитуды внешних кинематических возмущений z i , обеспечивающих необходимые требования к динамическим особенностям вибрационного поля; в — амплитуды колебаний вибрационного поля технического объекта в зависимости от частоты внешнего возмущения; г — варианты вибрационных полей в зависимости от весового коэффициента энергетического оператора T β
Механика
Совокупность внешних возмущений кинематического характера — это решение задачи минимизации энергетического функционала, в общем случае заданного на динамических состояниях механических колебательных систем с учетом требований к амплитудам колебаний в фиксированных точках вибрационного поля (рис. 4 б ).
Особенность вынужденных кинематических возмущений, обеспечивающих требуемую форму вибрационного поля, — возрастание амплитуды колебаний по мере роста частоты возмущений (рис. 4 в ). Внешние кинематические возмущения z обеспечивают на различных частотах ω фиксированное вибрационное поле технического объекта (рис. 4 г ). Параметр сглаживания α = 0,01 обеспечивает величину абсолютного отклонения от требуемых значений на уровне φ(α) = 0,000053. Это показывает, что совокупность амплитуд колебаний в остальных точках вибрационного поля определяет особенности энергетического оператора на основе необходимых значений амплитуд вибрационного поля в фиксированных точках механической колебательной системы. В частности, оператор T e направлен на формирование равномерного вибрационного поля, а оператор T E — на обнуление вибрационного поля.
Можно использовать весовые коэффициенты, отображающие комбинацию критериев оптимальности. Это позволит совместить:
-
- требования по сближению амплитуд колебаний точек вибрационных полей;
-
- требования, направленные на обнуление амплитуд колебаний точек вибрационного поля.
Варьирование весовых коэффициентов, определяющих комбинацию оптимальных критериев формирования вибрационного поля, фактически является способом коррекции вибрационного поля.
Построим семейство форм вибрационных полей технического объекта, удовлетворяющих определенным условиям. С этой целью используем комбинированный критерий оптимальности, реализуемый с помощью взвешенной суммы энергетических функционалов с учетом весового коэффициента:
II T 3 у\ I2 = \ее у I2 +р| \Те у I2 . (28)
Здесь β — весовой коэффициент, определяющий комбинацию критерия оптимальности на основе малости амплитуд и критерия на основе однородности амплитуд вибрационных полей. Варьирование весового коэффициента β приводит к построению семейства вибрационных полей. Критерий их оптимальности имеет сложную структуру, учитывающую разницы и абсолютные значения амплитуд колебаний точек вибрационного поля. Выбор совокупности весовых коэффициентов определяет соответствующие формы вибрационных полей, которые реализуются под воздействием внешних возмущений, являющихся решением вариационной задачи [20] .
На основе совокупности весовых коэффициентов β можно построить оптимальные вибрационные поля, с достаточной точностью удовлетворяющие требованиям к амплитудам колебаний в фиксированных точках (таблица 3).
Таблица 3
Формы оптимальных вибрационных полей для весовых коэффициентов энергетического функционала
|
№ |
β |
α |
Невязка φ(α), м |
Частота ω, рад/с |
y 1 , м |
y 2 , м |
y 3 , м |
y 4 , м |
y 5 , м |
|
1 |
1 |
0,01 |
0,0000841 |
10 |
0,0019704 |
0,0009850 |
0,0009845 |
0,0019686 |
0,0049213 |
|
2 |
0,5 |
0,01 |
0,0000503 |
10 |
0,0019847 |
0,0014467 |
0,0016322 |
0,0026337 |
0,0049521 |
|
3 |
0,25 |
0,01 |
0,0000305 |
10 |
0,0019940 |
0,0018969 |
0,0022740 |
0,0032196 |
0,0049701 |
|
4 |
0,125 |
0,001 |
0,0000195 |
10 |
0,0020000 |
0,0022503 |
0,0027818 |
0,0036611 |
0,0049980 |
|
5 |
0,0625 |
0,001 |
0,0000014 |
10 |
0,0020004 |
0,0024754 |
0,0031053 |
0,0039292 |
0,0049986 |
Комбинирование оптимальных критериев формирования вибрационных полей — это способ коррекции динамических состояний технического объекта (рис. 4 г ). Отметим, что найденные кинематические возмущения z i , рассматриваемые как функции частоты ω, имеют по одному нулю (рис. 5 е ).
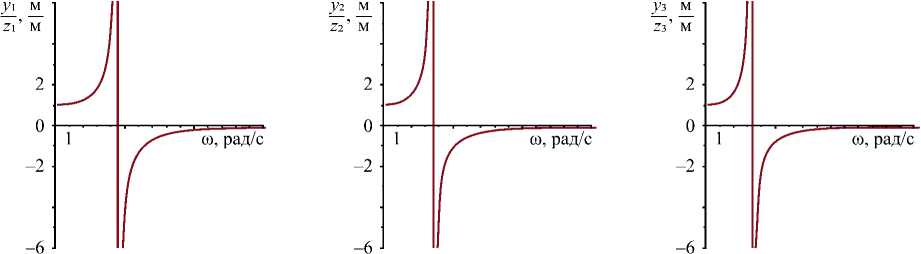
а ) б ) в )
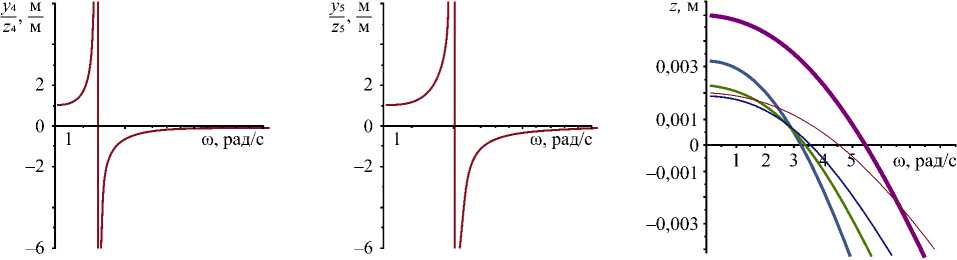
г) д ) е)
Рис. 5. Характеристики оптимального вибрационного поля для весового коэффициента в = 0,25 и параметра сглаживания а = 0,01: а — отношение амплитуд колебаний точек оптимального вибрационного поля (у а ) 1 к амплитуде кинематических возмущений (z a ) i ; б — отношение амплитуд ( у а ) ? к ( z а ) ? ; в — отношение амплитуд (у а ) з к ( z а ) з ; г — отношение амплитуд (у а ) 4 к ( z а ) 4 ; д — отношение амплитуд (у а ) 5 к ( z а ) 5 ; е — значение амплитуд внешних возмущений ( z а ) в зависимости от частоты и
Отношения амплитуд yi / z i , для которых yi = yi (ю) и z i = z i (ю) найдены на основе решения задачи определения оптимальных вибрационных полей, имеют по одному разрыву 2-го рода (рис. 5 а -д ).
Следует обеспечить заданные амплитуды колебаний фиксированных точек вибрационного поля механической колебательной системы. Для этого можно выбрать комбинированные энергетические функционалы с учетом весовых коэффициентов и, основываясь на данных показателях, определить необходимые внешние кинематические воздействия с учетом вариационных принципов.
Если требования к амплитудам колебаний вибрационного поля сильно зашумлены или несовместны, можно построить вибрационное поле, которое с определенной точностью удовлетворяет требованиям и является оптимальным для комбинированного критерия, но для других условий.
Определение оптимального критерия формообразования вибрационных полей на основе функции невязки. В общем случае требования к вибрационному полю могут представлять собой сложный комплекс совместных или несовместных условий, отражающих ограничения на амплитуды смещений, скоростей, динамических реакций, включая условия неудерживающего характера.
С учетом критерия оптимальности вибрационного поля механической колебательной системы совокупность совместных условий допускает единственное решение в форме определенной структуры внешних возмущений. В случае несовместности условий на вибрационное поле критерий оптимальности фактически выступает методом регуляризации некорректной обратной задачи.
Энергетический функционал определяет специфику формообразования вибрационных полей на основе значений амплитуд колебаний смещений, скоростей, силовых возмущений или реакций, возникающих между элементами системы. Энергетические функционалы могут передавать представления о максимальной потенциальной или кинетической энергии или служить их комбинацией с учетом весовых коэффициентов, выполняющих роль методов коррекции вибрационных полей.
К условиям по значениям амплитуд вибрационных полей возможно добавить условия по характеру самих внешних кинематических или силовых возмущений. Они выражаются в том, что амплитуды внешних возмущений принимают фиксированные абсолютные или относительные значения. Необходимость задания требований к входным возмущениям связана с тем, что для обеспечения заданных форм вибрационных полей амплитуды внешних возмущений могут неограниченно возрастать по мере роста частоты.
Механика
Итак, представим комплексную задачу выбора:
-
- энергетического функционала;
-
- оператора требований к вибрационному полю;
-
- дополнительного оператора требований к внешним силовым или кинематическим возмущениям.
В рамках развития структурной теории оптимального вибрационного поля можно поставить обобщенную задачу его построения:
у а ( го ) = arg min T e ( у ) ,
Ay=b,y=(-M ого2 + K) Kz ,Cz = f где C ■ z = f — дополнительная связь, ограничивающая размерность внешних кинематических возмущений.
Методология выбора эффективного оператора может базироваться на минимизации функции дополнительной невязки, зависящей от параметров энергетического оператора:
ро = argmin^Byр -с||2, где yβ — решение задачи определения вибрационного поля с комбинированным критерием оптимальности Tβ ((28) и рис. 4) и условиями A (10); В — оператор определения значений в совокупности дополнительных точек; c — вектор значений в дополнительных точках.
Эту задачу можно рассмотреть как задачу выбора «естественного» критерия оптимальности [21] . Таким образом, представленная совокупность задач и методов решений может быть фундаментальной основой структурной теории построения вибрационных полей.
Обсуждение и заключение. Разработаны элементы структурной теории оптимальных вибрационных полей механических колебательных систем. Основные компоненты указанной теории — это методы построения вибрационных полей механических колебательных систем на основе вариационных принципов. Основное понятие — вибрационное поле механической колебательной системы. Оно представляет собой распределение амплитуд колебаний обобщенных координат и других динамических характеристик механической колебательной системы по точкам объекта с оцениваемым динамическим состоянием.
Предполагается, что в ряде точек механической колебательной системы задана система условий. Она выражается через абсолютные или относительные значения смещений, скоростей и реакций. Условия — это требования к характеристикам вибрационного поля механической колебательной системы. Существует также система условий, связанных с особенностями внешних силовых или кинематических возмущений, и она тоже отражает требования к совокупности абсолютных и относительных значений амплитуд кинематических или силовых возмущений.
Для развития прикладной теории оптимальных вибрационных полей в рамках структурных представлений можно установить аналогию между двумя парами. Первая образована из оператора энергии T и оператора условий А в теории абстрактных сплайнов. Вторая образована критерием оптимальности вибрационного поля и системой требований к характеристикам вибрационного поля в контрольных точках.
В рамках теории вариационной сплайн-аппроксимации различают интерполяционные, сглаживающие и смешанные сплайны. В рамках представлений о вибрационных полях механических колебательных систем на основе структурных представлений роль сплайна выполняет совокупность амплитуд внешних силовых и кинематических возмущений, а роль интерполяционных условий выполняет совокупность требований к амплитудам входных или выходных сигналов.
Можно полагать, что существуют различия между вибрационными полями технических объектов, находящихся в условиях внешних возмущений силовой или кинематической природы, которые рассматриваются как ключевой фактор формирования динамического состояния. Вместе с тем, при построении вибрационного поля считается естественной оценка энергетических соотношений, зависящих от обобщенных координат. Их значения определяются по внешним силовым или кинематическим возмущениям. Фактически нужно найти два вектора — обобщенных координат и внешних возмущений.
Учтем вариационный подход, а также совокупность требований к вибрационному полю и внешним возмущениям. Представим задачу определения внешних возмущений, формирующих совокупность динамических состояний, в виде вибрационного поля с учетом системы условий. В такой интерпретации речь идет о задаче оптимизации в разных постановках в рамках вариационных принципов. В частности, возможны постановки задач, аналогичных задачам построения сглаживающего или смешанного сплайна. Это зависит от совместности условий на входные и выходные сигналы. Отметим существенную особенность задач построения вибрационных полей: частота внешнего возмущения — это параметр задачи оптимизации, а в случае с системами с сосредоточенными параметрами векторы амплитуд служат элементами n -мерного Декартова пространства.
Аналогии между задачами аппроксимации и построения вибрационных полей позволяют развивать методологии формирования, оценки и коррекции динамических состояний технических объектов.
Усовершенствованная структурная теория оптимальных вибрационных полей будет востребована в авиационной и космической промышленности. Ее аппарат можно применить для обеспечения безопасности полетов и долговечности конструкций. Кроме того, данный подход логично задействовать в машиностроении, электронике, при разработке медицинского оборудования. Теория позволит решать задачи формирования, оценки и коррекции состояний технических систем и устройств в условиях вибрационного нагружения. Еще одно направление ее практического применения — создание и улучшение измерительных способов и средств сложных колебательных систем. Полагаем также, что математические модели оптимальных вибрационных полей представляют интерес для разработки новых технологий и материалов, в частности, материалов с высокой амортизацией, которые могут снизить уровень вибраций и шума в технических системах.
В качестве основного ограничения методики необходимо указать, что рассматриваются колебания координат объекта, которые представляют собой установившиеся формы гармонических колебаний или колебаний фиксированной амплитуды.
Список литературы Оптимальные вибрационные поля в задачах моделирования динамических состояний технических объектов
- Juan Carlos A Jauregui Correa, Alejandro A Lozano Guzman. Chapter One — Fundamentals of Mechanical Vvibrations. Mechanical Vibrations and Condition Monitoring. Cambridge, MA: Academic Press; 2020. P. 1-26. https://doi.org/10.1016/B978-0-12-819796-7.00001-9
- Jalal Torabi, Jarkko Niiranen. Nonlinear Finite Element Free and Forced Vibrations of Cellular Plates Having LatticeType Metamaterial Cores: A Strain Gradient Plate Model Approach. Mechanical Systems and Signal Processing. 2023;192:110224. https://doi.org/10.1016/j.ymssp.2023.110224
- Keigo Ikeda, Kota Kamimori, Ikkei Kobayashi, Jumpei Kuroda, Deigo Uchino, Kazuki Ogawa, et al. Basic Study on Mechanical Vibration Suppression System Using 2-Degree-of-Freedom Vibration Analysis. Vibration. 2023;6(2):407-420. https://doi.org/10.3390/vibration6020025
- Большаков Р.С. Особенности вибрационных состояний транспортных и технологических машин. Динамические реакции и формы взаимодействия элементов. Новосибирск: Наука; 2020. 411 с. Bolshakov RS. Features of Vibration States of Transport and Technological Machines. Dynamic Reactions and Forms of Interaction of Elements. Novosibirsk: Nauka; 2020. 411 p. (In Russ.).
- Dumitriu M, Apostol II. Influence of Interference between Vertical and Roll Vibrations on the Dynamic Behaviour of the Railway Bogie. Vibration. 2022;5(4):659-675. https://doi.org/10.3390/vibration5040039
- Sehner M, Seidi-Nigsch M, Valdés Nava LE, Loy H. Vibration Mitigation: Under-Ballast Mats in Heavy-Haul Applications. Practice Periodical on Structural Design and Construction. 2023;28(4):05023004. https://doi.org/10.1061/PPSCFX.SCENG-1258
- Zhenhang Zhao, Ying Gao, Chenghui Li. Research on the Vibration Characteristics of a Track's Structure Considering the Viscoelastic Properties of Recycled Composite Sleepers. Applied Sciences. 2020;11(1):150. https://doi.org/10.3390/app11010150
- Yu Zou, Yongpeng Wen, Qian Sun. Study on the Urban Rail Transit Sleeper Spacing Considering Vehicle System. MATEC Web of Conferences. 2019;296:01008. https://doi.org/10.1051/matecconf/201929601008
- Yoshino Sh, Abe K, Koro K. An Analytic Solution of Mathematical Expectation for Bogie-Track Interaction Problems. Mechanical Engineering Journal. 2023;10(3):22-00300. https://doi.org/10.1299/mej.22-00300
- Wenping Chu, Yang Song. Study on Dynamic Interaction of Railway Pantograph-Catenary Including Reattachment Momentum Impact. Vibration. 2020;3(1):18-33. https://doi.org/10.3390/vibration3010003
- Maryam El Moueddeb, François Louf, Pierre-Alain Boucard, Franck Dadié, Gilles Saussine, Danilo Sorrentino. An Efficient Numerical Model to Predict the Mechanical Response of a Railway Track in the Low-Frequency Range. Vibration. 2022;5(2):326-343. https://doi.org/10.3390/vibration5020019
- Korendiy V, Kachur O, Predko R, Kotsiumbas O, Stotsko R, Ostashuk M. Generating Rectilinear, Elliptical, and Circular Oscillations of a Single-Mass Vibratory System Equipped with an Enhanced Twin Crank-Type Exciter. Vibroengineering Procedia. 2023;51:8-14. https://doi.org/10.21595/vp.2023.23657
- Krot P, Shiri H, D^bek P, Zimroz R. Diagnostics of Bolted Joints in Vibrating Screens Based on a Multi-Body Dynamical Model. Materials. 2023;16(17):5794. https://doi.org/10.3390/ma16175794
- Vishwa Priya Vellingiri, Udhayakumar Sadasivam. Effect of Vibrator Parameters and Physical Characteristics of Parts on Conveying Velocity. Strojniski vestnik — Journal of Mechanical Engineering. 2023;69(7-8):352-363. https://doi.org/10.5545/sv-jme.2022.510
- Korendiy V, Gursky V, Kachur O, Dmyterko P, Kotsiumba O, Havrylchenko O. Mathematical Model and Motion g Analysis of a Wheeled Vibro-Impact Locomotion System. Vibroengineering Procedia. 2022;41:77-83. S https://doi.org/10.21595/vp.2022.22422 §
- Krupenin V, Astashev V. Properties of Vibration Fields in a Two-Dimensional Lattice Structure Colliding with an Obstacle. In: EJ Sapountzakis, M Banerjee, P Biswas, E Inan (eds). Proc. 14th Int. Conf. on Vibration Problems (ICOVP). Singapore: Springer; 2020. P. 473-485. https://doi.org/10.1007/978-981-15-8049-9 30
- Karnovsky IA, Lebed E. Structural Theory of Vibration Protection Systems. In book: Theory of Vibration Protection. Cham: Springer; 2016. 708 p. https://doi.org/10.1007/978-3-319-28020-2 12
- Eliseev AV. Structural Mathematical Modeling Applications in Technological Machines and Transportation Vehicles. Hershey, PA: IGI Global; 2023. 288 p. https://doi.org/10.4018/978-1-6684-7237-8
- Sarah Saeed. Laplace Transform: Basics and Main Properties. In book: J Garcia (ed). Encyclopedia of Electrical and Electronic Power Engineering. Amsterdam: Elsevier; 2023. P. 645-651. https://doi.org/10.1016/B978-0-12-821204-2.00062-3
- Bezhaev AYu, Vasilenko VA. Variational Theory of Splines. New York, NY: Springer; 2001. 208 p. https://doi.org/10.1007/978-1-4757-3428-7
- Василенко В.А., Елисеев А.В. Абстрактные сплайны с натяжением как функции параметров энергетического оператора. Сибирский журнал вычислительной математики. 1998;1(4):301-311. URL: https://www.mathnet.ru/links/ be5b8fe7cfea1927a6fff34630f7de33/sjvm311.pdf (дата обращения: 11.12.2023).


