Оптимальный прием навигационных сигналов

На нынешний день существует проблема качества принимаемой навигационной информации. Одними из самых важных проблем при реализации приемников навигационных сигналов являются:

• -    большое время поиска сигнала;

• -    маленькая чувствительность принимаемого сигнала;

• -    погрешность принимаемого навигационного сигнала.

Все текущие программно-аппаратные алгоритмы основаны на поиске сигнала корреляционными функциями. Лишь ряд фирм использует помимо стандартных алгоритмов методы быстрого поиска. Для решения поставленных проблем (задач) дополнительно используется поиск с помощью быстрого преобразования Фурье. Формулы (1) и метод Фурье преобразования кратко описаны ниже.

2п i

Xk =ZN—1 XnwN, Wn = ^ , k = 0…N – 1,              (1)

1 N -1 - _kn x _k = _N ∑ _n X _N w _N .

Покажем, как выполнить дискретное преобразование Фурье за O( N ( p ₁ + … + p_n )) действий при N = p 1 p ₂ . . p_n . В частности, при N = 2 ⁿ понадобится O( N log( N )) действий.

Дискретное преобразование Фурье преобразует набор чисел a ₀ , …, a_{n– 1} в набор чисел b ₀ , …, b_{n –1} , такой, что b_i = ∑ ⁿ _j ^- ₌ ¹ ₀ a_j ε ^ij , где ε ⁿ = 1 и £ ^k = 1 и £ ^k # 1 при 0 <  k <  n . Алгоритм быстрого преобразования Фурье применим к любым коммутативным ассоциативным кольцам с единицей. Чаще всего этот алгоритм применяют к полю комплексных чисел (с ε = e ^{2π i / n} ) и к кольцам вычетов.

Основной шаг алгоритма состоит в сведении задачи для N чисел к задаче для p = N/q числам, где q - делитель N. Пусть мы уже умеем решать задачу для N/q чисел. Применим преобразование Фурье к наборам ai, aq+1, ., aq(p_1)+i для i = 0, 1, ., q - 1. Покажем теперь, как за O(Np) дей- ствий решить исходную задачу. Заметим, что bi = Z q=0 8i (X p=0 akq + j8kq ). Выражения в скобках нам уже известны – это i (mod p)-е число после преобразования Фурье j-й группы. Таким образом, для вычисления каждого bi нужно O(q) действий, а для вычисления всех bi – O(Nq) действий, что и требовалось получить [1].

Данный алгоритм производит поиск сигнала в спектральной области, а затем передает тот участок, где присутствует сигнал, в коррелятор, который в свою очередь ищет сигнал уже во временной области. Данное программное решение позволило значительно сократить время поиска сигнала, однако это затруднило программно-аппаратную реализацию и очень осложнило математический аппарат и алгоритм. Алгоритм быстрого поиска представлен на рис. 1.

Следует также отметить, что Фурье-преобразование обладает плохой частотнопространственной локализацией, а также сложными алгоритмами по последующей фильтрации полученных отчетов.

Применяемый сегодня алгоритм имеет недостаток, выражающийся в определённой избыточности вычислений [2], которую можно проиллюстрировать с использованием рис. 2. Объём предварительно накопленного массива

Оптимальный прием навигационных сигналов данных определяется длительностью интервала накопления и шагом поиска. Длительность шага поиска определяется видом дальномерного кода, а длительность интервала накопления – требуемыми характеристиками обнаружения. В то же время количество символов на периоде дальномерного кода фиксировано. Если длительность интервала накопления будет в два раза больше, чем длительность периода кода, возникнет определённая избыточность. На рис. 2 условно показан период накопления, содержащий два одинаковых 17 периода дальномерного кода (изображены в виде треугольников). При расчёте корреляционных интегралов для разных значений задержек опорный сигнал сдвигается и специфика описанного в предыдущем разделе алгоритма такова, что рассчитываются значения при всех возможных задержках в диапазоне [0, Т]. Так как период дальномерного кода в рассматриваемом случае в два раза меньше, опорный сигнал, сдвинутый на Т/2, совпадает с исходным. В результате одно и то же значение корреляционного интеграла рассчитывается два раза. На правой части рисунка изображён результат – рассчитанная функция содержит два одинаковых периода.

Как альтернатива Фурье-преобразованию, для устранения вышеобозначенных недостатков предлагается в качестве быстрого поиска использовать вейвлет-преобразования,

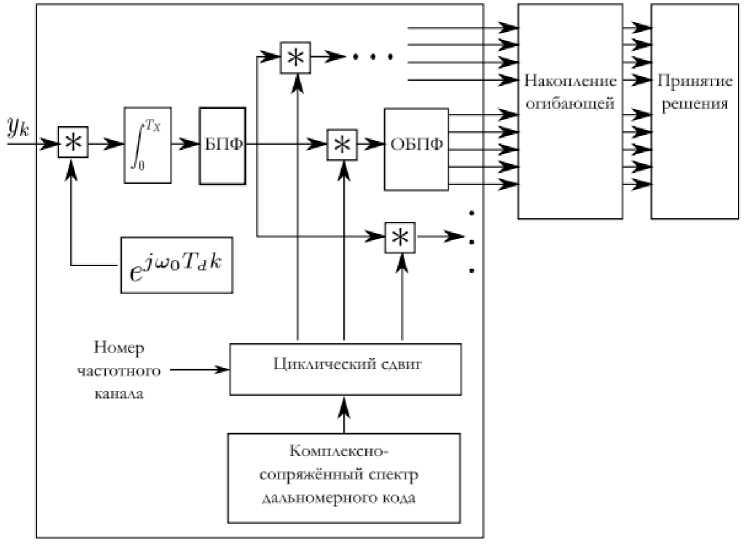
Рис. 1. Алгоритм быстрого поиска сигнала

■_■ ИССЛЕДОВАНИЯ

Havko-

Ограда

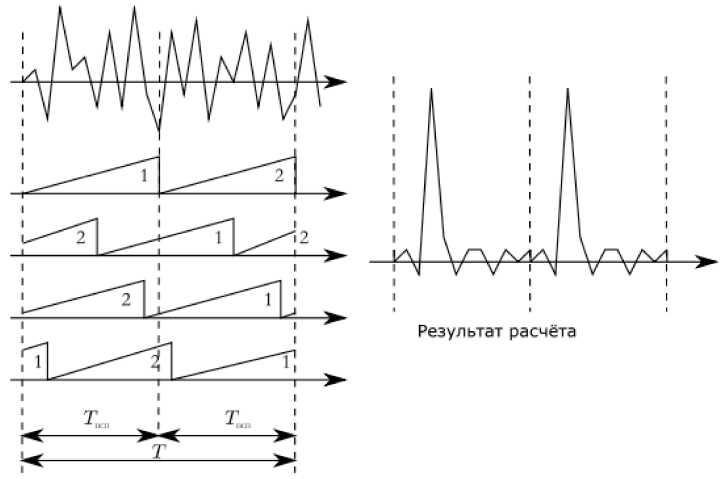
Рис. 2. Избыточность алгоритма быстрого поиска, основанного на быстрых преобразованиях Фурье

в частности лифтинг преобразования. Свойства вейвлет-функций – это разложить сигнал на ряд частотных фильтров, в основе которых лежит базисная функция (например, «Мексиканская шляпа», «прямоугольное окно» и т.д.). Формула (2) и метод вейвлет-преобразования применительно к мнимым и действительным сигналам кратко описаны ниже.

V mt ( t ⁾ = a m/2 V ( a m t + ^k ) ^{5 (} t ⁾ = ZL =-„ S mk V mt ⁽ t ).

Напомним условия точного восстановления для двух пар биортогональных фильтров. Рассмотрим две пары фильтров: ( h, g ) и ( h , g ) . Мы хотим проводить разложение при помощи свертки с ( h , g ) , а восстановление -при помощи ( h , g ) (в ортогональном случае h = h , g = g ). В терминах z-преобразования разложение на высокие и низкие частоты с прореживанием вдвое имеет вид, описанный формулой (3):

X ( z ) ^[ ( H l ( z ^ч) X ( z ) + H l ( - z "') X ( - z ))/2,

( G ( z ^{- l}) X ( z ) + G ( - z ^{- 1}) X ( - z ))/2 ] . (3)

Записав в аналогичном виде процесс восстановления с помощью пары ( h, g ) и приравняв результат к Х ( z ), получаем выражения (4), описанные ниже:

H ( z ) H ( z ^{- 1}) + G ( z ) G ( z ^{- 1}) = 2,

H ( z ) H ( - z ^{- 1}) + G ( z ) ( G ( - z ^{- 1}) = 0.    (4)

Метод лифтинга позволяет: 1) строить новые фильтры, удовлетворяющие выражениям (4), из уже имеющихся; 2) выполнять вейвлет-преобразование быстрее за счет декомпозиции на элементарные шаги лифтинга [3].

Следует отметить, что для поиска сигнала и оценки его наличия требуется не весь набор фильтров и отчетов (ФВВ, ФВН, ФНВ, ФНН), а только та часть, в которой обнаружен сигнал, для передачи его в коррелятор. Алгоритмически для внедрения в уже существующий алгоритм быстрого поиска, представленный на рис. 1, требуется заменить блок анализа сигнала, основанного на быстром преобразовании Фурье, на блок, в основе которого лежит вейвлет-анализ принимаемой информации.