Оптимальный выбор между плавным графиком и графиком регрессии в программе CurveExpert
Автор: Кагдин А.Н., Молоканов А.А., Энговатов В.П.
Журнал: Форум молодых ученых @forum-nauka
Статья в выпуске: 8 (24), 2018 года.
Бесплатный доступ
В статье рассмотрены различные способы аппроксимации графиков и последующий оптимальный выбор.
Оцифровка изображений, аппроксимация, интерполяция
Короткий адрес: https://sciup.org/140284027
IDR: 140284027
Текст научной статьи Оптимальный выбор между плавным графиком и графиком регрессии в программе CurveExpert
Senior lecturer of the department "Power engineering"
Molokanov AA
3rd year student
3rd year student
Tambov State Technical University
Russia, Tambov
OPTIMAL SELECTION BETWEEN A SMALL SCHEDULE AND A SCHEDULE OF REGRESSION IN THE PROGRAM CurveExpert
При применении программы CurveExpert были получены 2 основных графика с большим числом совпадений. График гладкой функции Савитского-Галея и график полиномиально-регрессивной функции.
Фильтр Савицкого–Голея - это цифровой фильтр, который применяется к набору цифровых данных в целях сглаживания данных, чтобы увеличить отношение сигнал-шум без существенного искажения сигнала. Это достигается, в процессе, известном как свертка, сопоставляя последовательные подмножества соседствующих точек, данных с низкой степенью полинома с помощью наименьших квадратов. Когда данные точки находятся на равном расстоянии, с аналитическим решением к уравнениям наименьших квадратов можно найти, в виде одного набора "коэффициентов свертки", которые применяются к абсолютно всем поднаборам данных, чтобы дать оценки сглаженного сигнала (или производные сглаженного сигнала) в центральной точке каждого поднабора. Метод, основанный на вышеизложенных математических процедурах был впервые открыт Авраам Савицким и Марселем Ж. Е. Голе, которые опубликовали таблицы свертки коэффициентов для дифферентных полиномов в 1964 году. Некоторые ошибки в таблицах были исправлены. Метод был расширен для обработки 2-и 3-мерных данных.
Фильтр скользящего среднего обычно используется с данными временных рядов для сглаживания краткосрочных колебаний и выделения долгосрочных тенденций или циклов. Он часто используется в техническом анализе финансовых данных, таких как цены на акции, доходность или объемы торгов. Он также используется в экономике для изучения валового внутреннего продукта, занятости или других макроэкономических временных рядов.
Невзвешенный фильтр скользящей средней является простейшим фильтром свертки. Каждое подмножество набора данных устанавливается прямой горизонтальной линией. Он не был включен в таблицы свертки коэффициентов как все значения коэффициентов не равны 1 .
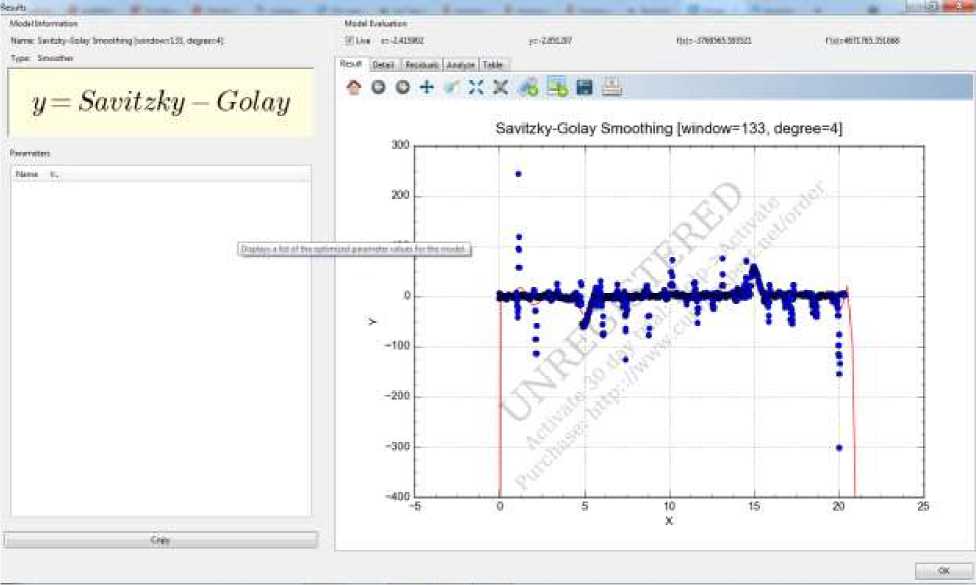
Рисунок 1 – гладкая функция Савитского-Голая
Выражаясь простым языком, модель регрессии в математической статистике строится на основе известных данных, в роли которых выступают пары чисел. Количество таких пар заранее определено. Если представить себе, что первое число в паре – это значение координаты x, а второе – y, то множество таких пар чисел можно представить на плоскости в декартовой системе координат в виде множества точек. Данные пары чисел берутся не случайно. На практике, как правило, второе число зависит от первого. Построить регрессию – это значит подобрать такую линию (точнее, функцию), которая как можно точнее приближает к себе (аппроксимирует) множество вышесказанных точек.
Полиномиальная регрессия может применяться в математической статистике при моделировании трендовых составляющих временных рядов. Временной ряд — это, по сути, ряд чисел, которые зависят от времени. Например, средние значения температуры воздуха по дням за прошедший год, или доход предприятия по месяцам. Порядок моделируемого полинома оценивается специальными методами, например, критерием серий. Цель построения модели полиномиальной регрессии в области временных рядов всё та же – прогнозирование.
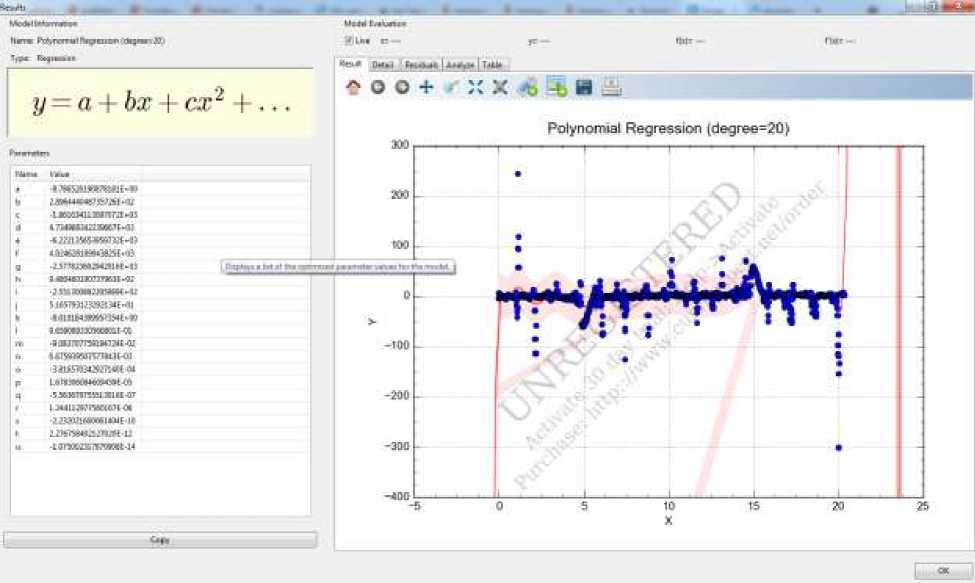
Рисунок 2 – полиномиальная регрессия
Цель аппроксимации состояла в том, чтобы получить уравнение графика для последующего занесения в базу данных, поэтому оптимальным выбор станет график полиномиальной регрессии.(рис. 2)
Список литературы Оптимальный выбор между плавным графиком и графиком регрессии в программе CurveExpert
- 1. Ю.Н. Шахов Численные методы : учебное пособие // Ю.Н. Шахов, Е.И. Деза // - М. - 2010 - с. 50-71


