Оптимизации плана транспортировки природных ресурсов и продуктов

OPTIMIZATION PLAN, TRANSPORTATION OF NATURAL RESOURCES AND PRODUCTS

В данной статьеописывается задача оптимизации     плана транспортировки природных ресурсов и продуктовза счет минимизации затрат на транспортировку.

Транспортировка природных ресурсов и продуктов – это строго регламентированный процесс, все этапы которого следует четко соблюдать во избежание несчастных случаев, которые могут повлечь за собой серьезные последствия и явиться причиной экологической катастрофы. Выбор транспортировки начинается с оценки технических характеристик природных ресурсов и продуктов. Если по техническим характеристикам продукцию можно перевозить любым видом транспорта, то тогда проводится анализ и расчеты самого выгодного способа транспортировки природных ресурсов и продуктов. Если же по каким-то характеристикам продукцию нельзя перевозить некоторым транспортом, то используется самый выгодный (в денежном эквиваленте) и подходящий. Для транспортировки природных ресурсов и продуктов используются различные способы, в частности магистральные нефтепроводы, автомобильный и воздушный, а так же железнодорожный и водный (морской и речной) транспорт.

В зависимости от типа продукта, который будет перевозиться, следует соблюдать те либо иные правила. В большинстве случаев требуется, чтобы емкости, в которых перевозятся жидкие природных ресурсов и продуктов, были оснащены внутренним покрытием, которое обеспечивает     необходимый     уровень     паростойкости     и маслобензостойкости.

Для решения задачи «формирование оптимального плана транспортировки природных ресурсов и продуктов » будет использоваться модель минимизации затрат на мероприятия транспортировки продукции, обслуживания транспорта во время транспортировки.

При решении данной задачи рассматривается один критерий оптимальности (минимизация затрат) – это затраты на транспортировку, которые для оптимального плана должны стремиться к минимуму [1]:

mm

Z         aijcijxj    min (1), j1j1

где Z – критерий оптимальности;

i=1, 2, 3, …,n – виды транспорта;

j=1, 2, 3, …,m – типы продукции;

с ij - стоимость i – го транспорта с j –й продукцией;

a ij – частота проведения i- го мероприятия для j- го транспорта;

x j – количество j- го продукта.

При формировании оптимального плана затраты на транспортировку природных ресурсов и продуктов и уходу за цистернами не должны превышать установленного лимита [3]:

mn aijcijxj P (2), j0i1

где c 0j – единовременные затраты на транспортировку j – ой продукции; a 0j =2, так как уход за цистернами производится дважды(при наливе и при разливе);

P – объем установленного лимита.

Единовременные затраты на транспортировку природных ресурсов и продуктов, включают в себя стоимость продукции (S m ), стоимость затрат на транспорт (S g ), оплату работ персоналу сопровождающему продукцию в пути (S r ), затраты на обслуживание цистерн с продукцией (S p ), а также транспортные расходы (S t ):

c 0j = S m + S g + S r + S p + S t    (3).

Расчет затрат на транспортировку какого- либо транспорта, исходя из километража, совпадающих заказов, производится путем правила сложения векторов [2].

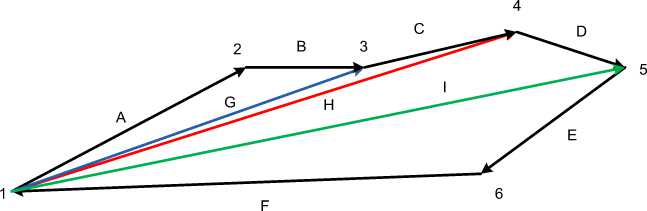
Рис. 1. Диаграмма Примера следования транспорта

G A B - путь из пункта 1 в пункт 3 с учетом доставки продукции в пункт 2.

Результирующий вектор пути:

——     —►                ——

R A ...... Fn (4)

где R — - результирующая сумма километража

Затраты на транспортировку нескольких заказов, совпадающих по маршруту, не должны превышать их затраты по отдельности [1]:

mn bijxj   T (5), j1i0

где b ij – затраты на транспортировку i- ой продукции, нескольких заказовi-ой продукции;T – суммарные затраты на транспортировку нескольких заказов, совпадающих по маршруту.

Так как должны быть транспортированы разнообразные виды продукции с разными характеристиками по перевозке и хранению, то задается соотношение относительно объема транспортируемой продукции.

где    l j

–

kj x lj j

коэффициент,

k1 x1   0, j 1,m (6), l1

задающий соотношения по объему

транспортируемой продукции. Коэффициент l j лежит в пределах между нижней и верхней границами:

l j^min ≤ l j ≤ l j^max (7).

Следовательно, получается система ограничений:

kj min kj max

xj - k1x1

l1

x - k1 x 0

j l1

j

На объем продукции накладывае тся у словие на неотрицательность. x_j   0 , j 1 ,m ( 9 )

Стоимость на i шаге эксплуатации составляет

Z i    P 0   k j P 0   i 1   (10)

где Р 0 – начальная стоимость продукции, руб.

i – номер шага.

k _j – параметр амортизации.

А также объем продукции должен быть целым числом: x j – целые.

В результате математическая модель будет выглядеть следующим образом:

Z m n aijcijxj    min (11)

j1i1

при выполнении системы ограничений:

mn aijcijxj j1i0

—    ———

R A  Fn mn bijxj j1i0

kj x -  1 x 0, j 1,m min j1

lj

kk x -  1 x 0,j1,m max j1

lj xj   0,j1,m

• 7 - р -L V . Р . *— 1

Zi P0 kj P0 i1

St Z 2t x целые

Данная система уравнений поможет решить поставленную задачу «Оптимизация плана транспортировки природных ресурсов и продукции», найти оптимальный план транспортировки, минимизирующий затраты.

Inthis paper we considerthe problem of choosingthe optimal planof transportationof natural resources andminimizingproductcosts.With the help ofa mathematical modelisconstructed bythe solution to thisproblem.