Оптимизация адгезионной прочности композиции металл - полимер

Прогресс во многих областях техники непрерывно связан с проблемами создания и внедрения эффективных защитных полимерных покрытий, способных работать под нагрузкой и в различных условиях эксплуатации.

Для защиты металлических элементов автомобильного транспорта при длительной эксплуатации успешно применяют полимерные покрытия, которые являются универсальным видом защитным металла от коррозии.

Основным условием работоспособности композиции металл – полимер является сохранение сплошности покры-элемента, температура, физикохимическое воздействие внешней среды, тия, так как образование любого сквозного дефекта в полимерном покрытии приводит к нарушению адгезионной связи и появлению коррозии металла.

При изучении прочности полимерных покрытий обычно рассматривают два основных вида разрушения – адгезионное и когезионное [1]. Тот или иной вид разрушения, а также смешанное адгезионно – когезионное разрушение обусловлено рядом внутренних и внешних фактов, таких как прочность, химический состав и структура полимерного покрытия и металла, вид напряженного состояния, геометрическая форма физико-химическое взаимодействие в контактной зоне при формировании и эксплуатации покрытия и др.

Одним из главных условий работоспособности полимерного покрытия является достаточная прочность сцепления его с металлом. В зависимости от соединения фаз и условий формирования композиции природа связи между поли- мерным покрытием и поверхностью металла может быть различной [2].

В связи с этим представляем интерес исследование оптимизации адгезионной прочности композиции металл- полимер.

Рассмотрим одноосное растяжение металлической пластины, на боковых поверхностях которой нанесено полимерное покрытие толщиной h (рис). Задача сво- дится к определению напряжения в любом соединение покрытия и металла. Начало координат выбрано в средней точке оси пластины. Сечение Z=0 остается при деформировании плоским. Нагрузка при- кладывается только к торцам металла. Поэтому напряжение в покрытие возни- кает только из-за касательных напряжений на поверхности адгезионнойго контакта с металлом. Принимаем во внимание также, что линейные элементы при деформации остаются прямыми. Решение такой задачи получено в работе [3]. Согласно этой работы касательные напря- жения т в поверхностном слое металла и нормальные напряжения в покрытии определенной из соотношений:

т = —

Ем'К 1    ,    2

WFn

^п

Fn(;

I e_m-f_m

Ем 1     ,     2

-En-F,

К2

= 2tLQ

Ем'Ем

1 ,

sh/cz chkz ’ sh/cz.

) ch/cz

2 ч

£п*£п E_m*F_m

где: Еп, Ем - модули упругости покрытия и металла соответственно; Fп, Fм - пло- щади покрытия и металла соответсвенно;

sh/cz, chkz - гиперболические синус и косинус от аргумента kz.

Для пластин большой протяженности по ширине, с учетом эффекта Пуассона, в формулах для напряжения (1) и (2) вместо величин Е п и Е м подставляем величины Е п /(1-Дп) и Е м (1-ц_м).

Принимаем условие адгезионной и когезионной равнопрочности композиции металл - полимер. Для этого рассмотрим когезионное разрушение полимерного покрытия под действием нормальных напряжений , вызванных критической деформацией металла    . Эти величи ны связаны зависимостью (2), а напряжения оп в момент разрушения равны пределу прочности материала покрытия, т.е.

. Величина адгезионной прочности будет оптимальной, когда максимальные касательные напряжения на образовавшиеся в результате разрушения кромки полимерного покрытия будут равны пределу прочности сцепления, т.е. при достижении металлом критической деформации еМкр произойдет одновременное когезионное разрушение покрытия и его отслоение в зоне образовавшейся трещины.

В связи с этим, для оптимального соотношения адгезионной и когезионной прочности полимерного покрытия в зависимости от критической деформации металла £Мкр необходимо определить эти величины из зависимостей (1) и (2).

Определяем максимальные касательные напряжения из уравнения (1) при Z=L для пластины единичной ширины ( < =1):

„ ^- -ML . (4) ^сп ^гп ^ьм ^гм

В большинстве случаев при нанесении полимерного покрытия на металлическую поверхность имеем Е_п- Е_п . Тогда

Учитывая, что на достаточном удаление от кромки при когезионном разрушении соблюдается равенство °пв ^Пкр ' ^п , а также ^сц ^тах , получаем условие адгезионной и когезионной равной прочности:

^ = h_k thkL .             (6)

Критическую деформацию металла определяем из выражения (4): тсц /

Е»«р = -gr          (7)

и получаем зависимость для определения минимально допустимой прочности сцепления для случая статического растяжения композиции металл – полимер:

т_сц ^MKpt^fcL ¹ E^h^ .      (8)

Остаточные нормальные напряжения в полимерном покрытии G_n и металле G_M определяет по формулам, предложенным С.П. Тимошенко [4] и уточненным в работах [5,6]:

^Сп=1? [^^ ^ " /п + ^м ' /м) ^  ~];

СТМ = "^Т [^^ (^п ■ /п + Ем • /м) Н  — ] , где: ^п> ^м – толщина полимерного покрытия и металла соответственно; h– общая толщина композиции металл – полимер; 8 – прогиб образца композиции; b – ширина образца композиции; 7п 12 , ^м — 12 – моменты инерции полимерного покрытия и металла соответственно.

Результаты проведения исследования можно использовать в конструкторской практике при выполнении расчетов на прочность композиционных элементов металл – покрытие по предельным и остаточным напряжениям, а также деформациям металла, вызывающим отслоение полимерного покрытия от металлической поверхности.

Известно [1], что работа клеевого металлополимерного соединения глав- ным образом определяется релаксационной способностью клеевого слоя, то есть является следствием деформационной способности, которую в условиях работы клеевого слоя проконтролировать практически невозможно. Выбор критерия прочности для клеевого металлополи-мерного соединения необходимо проводить с учетом структурных изменений, которым подвергается клеевой слой в процессе эксплуатации в составе изделия, и большого количества экспериментальных данных.

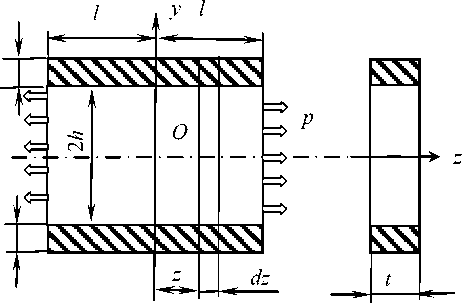
Рисунок – Расчетная схема для определения нормальных напряжений в полимерном покрытие а_п и касательная напряжения т_в в зоне адгезионного контакта композиции металл – полимер .

При выборе критерия прочности для клеевых металлополимерных соединений на основании [7,8] отдадим предпочтение критерию наибольших касательных напряжений, т.е. третьей теории прочности, которую с учетом исследуемых значений нормальных и касательных напряжений рассматриваем в виде:

°эквкр = Vo2 + 4т2 < [ст] (10)

Сравнение результатов расчета, выполненного с помощью зависимости (10), с экспериментальными данными, приведенными в работе [7], показало практически полное их совпадение, то есть факти- ческие данные хорошо согласуются с расчетными.

Это позволяет сделать вывод, что работу исследуемых клеевых металлополи-мерных соединений можно рассматривать в рамках основных положений третьей теории прочности при наличии большого количества экспериментальных данных. Кроме того, работа этих соединений аналогична основным особенностям работы пластических материалов.

Используя результаты исследований, приведенные в работах [1,7] проведен сравнительный анализ диаграмм предельного напряженного состояния клеевого металлополимерного соединения, который показал, что предельные кривые для различных длительностей предварительной нагрузки можно рассматривать как эквидистантные по отношению к диаграмме предельного напряженного состояния, полученной по результатам кратковременных статических испытаний [8]. Это дает возможность по диаграммам кратковременной прочности описывать диаграммы предельного напряженного состояния после различной предварительной наработки. Для этой цели в зависимость (10) введем временный коэффициент, а оценку эквивалентного напряжения после различной предварительной наработки будем выполнять по следующему выражению:

^KBt = ^тл/п2 + 4, (11)

^где n =<^/Т; Q-t ^ЭКВ[/^ЭКВ_кр-

В результате экспериментальных исследований были получены зависимости коэффициента at от величины соотношения нормальных и касательных напряжений для клеевого металлополимер-ных соединений, нагруженных предварительными нагрузками величина которых составляла 0,25 Ркр, и 0,5 Ркр. Анализ полученных данных позволил сделать заключение, что величина коэффициента at является постоянной для различных соотношений нормальных и касательных напряжений. Это дает возможность более точно выполнять сопоставление влияния рассматриваемого эффекта степени снижения кратковременной статической прочности после предварительной наработки клеевого металлополимерного соединения. Результаты сопоставления для стали Ст.3 при напряжениях о = 0,25 ов и а=0,5 ов (соответствующих 0,25 Ркр, и 0,5 Ркр), различных толщинах армированного клеевого слоя (0,5; 1,5; 2,5 мм) на основе клеевых композиций типа "Спурт-9М" и "ВАК-А" представлены в табл.1. В качестве армирующего материала здесь применялась стеклоткань марки Т-11-ГВС-9.

Таблица 1 - Результаты сопоставления

№ п/п	Толщина армированного полимерного слоя, мм	Минимальное значение at
		Клеевая композиция
		«ВАК-А»	«Спрут-9М»
1.	0,5	0,47/0,57	0,42/0,52
2.	1,5	0,55/0,64	0,48/0,58
3.	2,5	0,43/0,54	0,37/0,45

Примечания: в числителе при предварительной нагрузке 0,2 5 Р _кр ; в знаменателе при предварительной нагрузке 0,5 Р _кр .

Из табл.1 видно, что величина коэффициента a_t зависит от толщины армированного полимерного слоя и предварительной нагрузки. Результаты исследований позволили установить, что величина коэффициента a_t для армированного полимерного слоя на основе клеевой композиции типа "ВАК-А" примерно на 10% выше, чем для армированного полимерного слоя - "Спрут-9М". Кроме того, наблюдается идентичное снижение прочности для армированного полимерного слоя на основе клеевых композиций типа "ВАК-А" и "Спрут-9М".

Из литературы известно [1,5,6], что величину коэффициента d^ можно определить по результатам стандартных испытаний на нормальный отрыв или сдвиг. Проведенные исследования позволяют нам сделать вывод, что диаграммы предельного напряженного состояния клеевого металлополимерного соединения для заданного времени предварительной наработки и условий испытаний можно описать с помощью третьей теории прочности, зная величину коэффициента ^t , то есть рассмотренные диаграммы могут служить своеобразным эталоном, к достижению которого следует стремиться при разработке новых рецептур клеевых композиций и получении на их основе армированных полимерных покрытий.

Необходимо также отметить, что современное состояние науки позволяет теоретически и экспериментально оценить напряженное состояние поверхности склеивания, то есть определить величины нормальных и касательных напряжений, которые будут совместно передаваться клеевому металлополимерно-му соединению в составе изделия. Выполнив испытания прочности клеевого металлополимерного соединения на основе различных клеевых композиций при совместном действии нормальных и касательных напряжений в условиях, моделирующих реальные, построив по результатам этих испытаний диаграммы предельного напряженного состояния, можно оценить применимость армированного полимерного покрытия на основе любой клеевой композиции в конкретном клеевом изделии, то есть данные результаты исследований целесообразно использовать в конструкторской практике.

Кроме того, выявленная применимость критериев прочности для материалов, неодинаково сопротивляющихся растяжению и сжатию, к металлополи-мерным свидетельствует о принципиальной возможности расчета диаграмм их предельного напряженного состояния по результатам стандартных испытаний на прочность при нормальном отрыве и сдвиге.