Оптимизация бинарного ДОЭ для формирования "световой бутылки"

Оптической ловушкой типа «световая бутылка» (“light bottle”) называют такое распределение интенсивности лазерного излучения, в котором область нулевой интенсивности окружена световым барьером [1–3]. Одно из применений «световых бутылок» – захват холодных атомов или молекул [4].

Оптические ловушки основаны на силе, которая действует на атомы в поле со смещённой частотой излучения. В световом поле, настроенном выше резонанса, атомы выталкиваются из областей высокой интенсивности, в то время как при настройке ниже резонанса атомы притягиваются в эти области [5]. Во внерезонансных оптических ловушках используется настройка далеко от резонанса. Разрушительное действие нагрева на захваченные объекты является одной из основных проблем: даже помещение слабопоглощающих диэлектрических частиц в относительно прозрачную среду приводит к их повреждению при высоких оптических интенсивностях.

Альтернативой является захват в области с минимальной интенсивностью.

Одним из способов формирования областей с минимальной интенсивностью является использование лазерных пучко в с винтовой фазовой сингулярностью. Такие пучки несут угловой момент, связанный с вихревой структурой волно вого фронта, даже при линейной поляризации света. В [6] экспериментально демонстрируется 3D захват менее плотных, чем окружающая среда частиц (полые стеклянные шарики 20 мкм в диаметре в воде) с помощью одного, сильно сфокусированного кольцевого (полого) пучка. Захват происходит в осевой тёмной части пучка. При этом частицы с высоким показателем преломления были захвачены тем же пучком в кольце с высокой интенсивностью.

В области лазерного охлаждения и захвата нейтральных атомов полые пучки также представляют интерес из-за отталкивающего (от областей высокой интенсивности) действия оптической дипольной силы в поле лазера, настроенного выше резонанса («синяя расстройка»), позволяющего ограничить движение атомов в тёмной внутренней части полого пучка и формировать пучки медленных атомов для реализации возможностей атомной оптики. Такие ловушки имеют преимущество по сравнению с захватом в области высокой интенсивности лазерного поля, настроенного ниже резонанса («красная расстройка»), т.к. в этом случае минимизируются нежелательные эффекты, такие как нагрев при рассеянии фотонов и возмущения энергетических уровней световыми сдвигами.

В [7] ловушка с полым пучком Гаусса-Лагерра высшего порядка была реализована для атомов рубидия. В [8] описываются результаты по формированию полого пучка с помощью аксикона, дополненного сферической линзой (в фокальной плоскости которой получается узкое кольцо) для экспериментального исследования холодных атомов. Однако в этом случае резкое кольцо формируется только на узком продольном отрезке, так что захват будет слабым за пределами этого участка. В [9, 10] была показана возможность захвата и вращения частиц в вихревом бесселевом пучке, сформированном с помощью дифракционного спирального аксикона. Протяжённость такого полого пучка значительно превышает расстояние Рэлея для гауссовых пучко в и тем более фокальную глубину.

Лазерные пучки с вихревой фазовой сингулярностью проще всего формируются с помо щью дифракционных элементов, таких как спиральные фазовые пластинки [11-13]. Изготовление таких элементов достаточно сложно [14], а погрешности изготовления приводят к нарушению структур ы волнового фронта [15].

Известны способы бинарного кодирования дифракционных элементов, предназначенных для формирования оптических вихрей [5, 16]. При наложении линейной несущей функции производятся несколько (два и более) вихревых пучков, распространяющихся под углами к оптической оси. В этом случае количество энергии в каждой ловушке уменьшается пропорционально количеству формируемых пучков [17].

Отметим, что ловушки, основанные на п учка х с винтовой фазовой сингулярностью, вообще говоря, являются двумерными ловушками, т.к. теневая область ограничивается только поперечным световым барьером. При использовании же «световых бутылок» обеспечивается 3D-захват поглощающих и менее плотных, чем окружающая среда частиц.

В [1] формирование теневого фокуса осуществлялось с помощью введения фазового сдвига на π радиан центральной части фокусируемого гауссового пучка по отношению к периферии. Интенсивность «стенок» такой ловушки является довольно низкой.

В [2] рассматривалась интерференция мод Гаусса-Лагерра, фазовый сдвиг между которыми подобран так, чтобы при интерференции они взаимоуничтожа-лись в общем фокусе. Суперпозиция формировалась с помощью амплитудной голограммы, которая характеризуется низкой дифракционной эффективностью.

Аналогичная интерференция, но пучков с различной кривизной, была рассмотрена в [3]. Для этого использовался интерферометр, что, безусловно, усложнит и сделает оптическую систему микроманипулирования более громоздкой. Этим же недостатком обладают схемы с использованием двух оптических элементов – линзы и аксикона [18-20], хотя параметры ловушки можно динамически менять за счёт изменения расстояния между двумя этими элементами [19].

Требования компактности и простоты использования стимулируют развитие методов для синтеза одного оптического элемента, обеспечивающего заданное 3D распределение интенсивности. С помощью итерационных методов и методов кодирования [21-27] обеспечивается синтез высокоэффективных фазовых дифракционных оптических элементов (ДОЭ), предназначенных для генерации заданной суперпозиции многомодовых лазерных пучков. В частности, суперпозиция соосных бесселевых пучков [2627] позволяет формировать периодическую цепочку максимальных и минимальных значений интенсивности на оптической оси, т.е. продольный набор оптических «пузырьков». Таким образом, с помощью одного ДОЭ можно формировать определённую интерференционную картину как в поперечном, так и продольном направлениях. Однако, как было указано выше, технологии изготовления ДОЭ всё ещё несовершенны и хорошо отработаны лишь для бинарных вариантов, причём желательно, чтобы размеры зон значительно превышали длину волны (для оптического диапазона порядка микрона).

Одним из подходов к расчёт у бинарных ДОЭ , обеспечивающи х заданное распределение интенсивности в некоторой плоскости, поперечной к оси распространения (например, фокальной) или вдоль оптической оси, является разбиение элемента на кольцевые зоны с постоянной фазой [28-33]. В этом случае, разумеется, можно управлять распределением только в одном из выбранных направлений.

В данной работе предлагается иной метод расчёта бинарных кольцевых фазовых ДОЭ, основанный на применении генетического алгоритма и обеспечивающий эффективное формирование светового распределения в виде заданной 3D картины, полученной вращением одномерных распределений в нескольких плоскостях [34, 35]. В отличие от итерационных методов, использующих для этого суперпозицию бесселевых п учков, рассматриваемый подход одновременно учитывает ограничения на топологию дифракционного микрорельефа (в нашем случае -бинарный и радиально-симметричный), позволяет варьировать соотношение интенсивности светового барьера оптической ловушки в различных направлениях и управлять формой теневой области.

Полученные в [36-41] решения задачи расчёта радиально-симметричных ДОЭ, формирующих заданные распределения интенсивности, могут быть использованы в качестве начальных приближений для генетического алгоритма.

Описание вычислительного эксперимента

Постановка задачи оптимизации ДОЭ, формирую щего «световую бутылку» на расстоянии F1 от ДОЭ, представлена на рисунке 1.

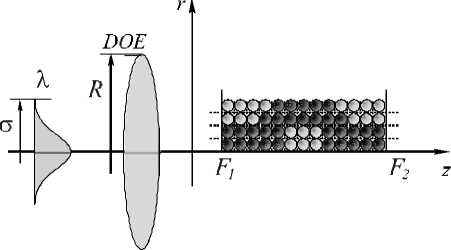
Рис.1. Оптическая схема формирования «световой бутылки»

Радиально-симметричный ДОЭ рассчитывался в рамках параксиального приближения. Область фокусировки была представлена в виде набора ди-λf фракционных пятен размером ∆ =   , где λ – длина

2R волны осве щаю щего п учка, f – расстояние от плоскости установки оптического элемента, R – радиус апертуры ДОЭ. В о бласти формирования заданного распределения яркость каждого дифракционного пятна выбиралась из соображения функционального назначения элемента – формирование затемнённой области на оптической оси, окружённой областями с высоким уровнем интенсивности. На рис. 1 более яркими пятнами обозначены участки высокой интенсивности, а менее яркими - участки низкой интенсивности. Взаимное расположение дифракционных пятен вблизи оптической оси, яркость в которых контролировалась в процессе расчёта, представлено на рис. 2.

Были выбраны следующие параметры оптимизации бинарного оптического фазового элемента: гауссов освещающий п учок с длиной волны λ=633 нм и радиусом перетяжки σ=0,5 мм, число уровней квантования микрорельефа M=2, число отсчётов вдоль радиуса N=200. Область формирования заданного светового распределения располагается вдоль оптической оси на расстоянии от F1=50 мм до F2=55 мм от плоскости установки элемента; область низкой интенсивности (внутренняя область оптической ловушки) имеет длину 2 мм.

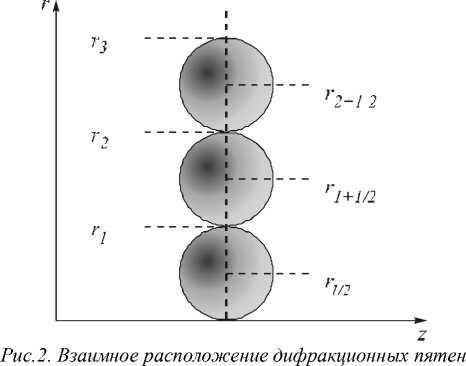
вблизи оптической оси, r n = n А

В качестве эталонного распределения интенсивности было принято распределение, представленное на рис. 3. Сплошной линией показано заданное распределение интенсивности ближайшего к оптической оси дифракционного пятна в зависимости от расстояния от плоскости установки ДОЭ, прерывистой линией – второго от оптической оси дифракционного пятна.

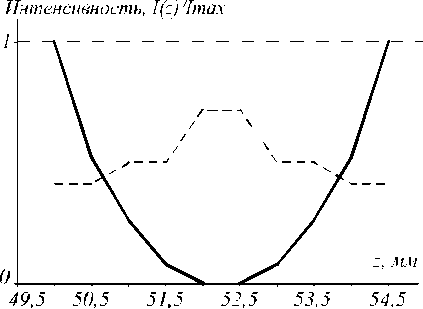
Рис.3. Заданное распределение интенсивности. Сплошная линия – заданная интенсивность первого дифракционного пятна, пунктирная – второго дифракционного пятна

альное расстояние от оси до центра дифракционного пятна, I _ср – средний уровень заданной интенсивности I ( z i , r j ) по области формирования ловушки, c i -коэффициент, учитывающий спад уровня интенсивности по мере удаления от источника излучения (выбор значения этого коэффициента позволяет управлять соотно шением значений интенсивности на оптической оси непосредственно перед теневой областью и за ней).

В данном функционале был использован метод экспоненцирования для лучшей сходимости алгоритма. Выбор коэффициента c_i (2) позволил «выровнять» правый и левый максимумы интенсивности первого дифракционного пятна (рис. 3).

Отметим сильную зависимость эффективности применения генетического алгоритма к минимизации функционала (1) от конфигурации алгоритма – в частности, от значений вероятности применения генетических операторов (мутации и скрещивания) [35].

В результате работы оптимизационного алгоритма была получена фаза бинарного ДОЭ, формирующего световое распределение типа «световая бутылка». Фазовая функция представлена на рис. 4. Белый цвет соответствует значению фазовой функции π, чёрный цвет – 0.

В ходе работы оптимизационного алгоритма минимизировался функционал:

Рис. 4. Фазовая функция ДОЭ, формирующего световое распределение типа «световая бутылка»

/

^ф( zi, rj ) = ci'

exp

к

' I ( z , r )^- I ( z , j

A A

к

I ( z i , rj]

1 ,

если I ( z i , r i ) >  0

^ф( zi, r) = ci*

exp

к

' I ( z , rA

A A

к

I ср

1,

если I ( z i , r ) = 0

где c i = exp 12

к

Z l I z 1 7

- 1

,

где I ( z i ,r j ) – интенсивность,

которую формирует

ДОЭ в точке ( z i , r j ) , I ( z i , r j ) - заданный уровень интенсивности в точке ( z i , r j .) , z i - расстояние на оптической оси от источника излучения, r j – ради-

На рис. 5 изображено распределение интенсивности, формируемое рассчитанным ДОЭ (результат моделирования), с наложенным эталонным распределением. На рис. 6 изображено распределение интенсивности первых четырёх дифракционных пятен, формируемых рассчитанным ДОЭ.

На рис. 7 a приведено двумерное распределение интенсивности, формируемое рассчитанным ДОЭ (результат моделирования, негативное изображение). На рисунке 7 b приведено распределение интенсивности в области формирования «световой бутылки», рассчитанное с помощью преобразования Френеля.

Численное моделирование показало, что средняя дифракционная эффективность [42,43] формирования заданного радиально-симметричного распределения интенсивности на всей протяжённости фокальной области вдоль оптической оси составило около 22%.

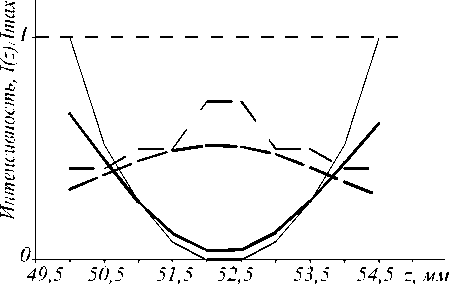
Рис. 5. Распределение интенсивности, формируемое рассчитанным ДОЭ. Толстые сплошная и пунктирная линии – сформированное рассчитанным ДОЭ распределение интенсивности первого и второго дифракционных пятен, соответственно. Тонкие сплошная и пунктирная линии – эталонное распределение интенсивности первого и второго дифракционных пятен, соответственно

Заключение

Результаты вычислительных экспериментов показали целесообразность применения предложенной численной оптимизационной процедуры к расчёту бинарных дифракционных оптических элементов, формирую щих световое распределение типа «световая бутылка».

К достоинствам рассмотренного подхода следует отнести то, что рассчитанные предложенной процедурой бинарные радиально-симметричные ДОЭ относительно просты в изготовлении.

Кроме того, предложенная процедура предоставляет возможности управления соотношением интенсивности «светового барьера» оптической ловушки в различных направлениях.

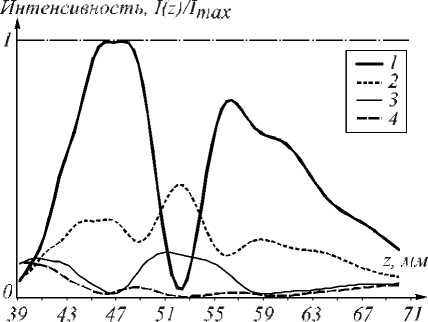
Рис. 6. Распределение интенсивности первых четырёх дифракционных пятен, формируемое рассчитанным ДОЭ (результат численного моделирования)

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и выс шее образование» (грант CRDF PG08-014-1), гранта Президента РФ поддержки ведущих научных школ НШ-7414.2010.9, ФЦП «Научные и на учно-педагогические кадры инновационной России» (госконтракт № 14.740.11.0041), грантов РФФИ 10-07-00109-а, 10-07-00438-а.