Оптимизация бинарных ДОЭ для формирования продольных распределений интенсивности

Элементы дифракционной микрооптики, формирующие заданные продольные распределения интенсивности (соосные отрезки, наборы последовательных осевых фокусов и т.д.), находят применение во многих областях техники. Например, при выравнивании и совмещении конструкций на больших расстояниях [1]; при формировании изображений протяженных или движущихся объектов, что особенно актуально в медицине [2-4], а также для неразрушающего исследования материалов [5] и устройств [6], в метрологии для сканирующих [7] и интерференционных [8, 9] оптических систем.

Классическим рефракционным оптическим элементом для генерации осевой световой нити является аксикон [10]. Однако распределение интенсивности вдоль оси, формируемое аксиконом, очень неравномерное – кроме существенных флуктуаций наблюдается линейный рост интенсивности при ув еличении расстояния от оптического элемента.

Оптимизация фазовой функции дифракционного оптического элемента, фокусирующего лазерное излучение в продольный отрезок, в рамках геометрооптического подхода рассматривалась в работах [11-13]. Отметим, что геометрооптический расчет принципиально не позволяет учесть дифракционных эффектов.

Также известны итерационные методы расчета ДОЭ [14], основанные на алгоритме Герчберга-Сакстона [15], которые позволяют учитывать дифракционные эффекты, однако не обладают сходимостью (может быть показана лишь нерасходи-мость). Кроме того, необходимость применения обратного оператора на каждой итерации метода затрудняет получение квантованной фазы оптического элемента, в то время как значительная часть технологий (главным образом литографических) ориентирована как раз на получение квантованного микро- нанорельефа [16]. Поэтому в работе [17] для синтеза бинарного рельефа был применен метод последовательных приближений с бинаризацией фазовой функции на каждом шаге. Полученный ДОЭ имел вид кольцевой решетки из 186 колец, причем на периферии период был близок к 10 мкм при радиусе элемента 4 мм.

В случае, когда шаг поперечной дискретизации должен быть не меньше определенной величины, и соответственно, количество колец в структуре ДОЭ желательно свести к минимуму, предпочтительнее применение стохастических алгоритмов прямого поиска, так как поиск функции высоты микрорельефа можно организовать на множестве квантованных решений, к тому же алгоритмы прямого поиска обладают сходимостью.

В работах [18, 19] обсуждался расчет бинарных ДОЭ, формирующих множество фокусов, а также фокусирующих в заданные кривые в электромагнитном приближении. Однако при формировании осевых световых распределений, удовлетворяющих параксиальному приближению, применение скалярной теории дифракции является вполне корректным и ресурсосберегающим подходом.

Данная работа посвящена стохастической оптимизации квантованных дифракционных оптических элементов, предназначенных для формирования заданных продольных распределений интенсивности.

1.    Основной формализм

Рассмотрим постановку задачи расчета ДОЭ, формирующего продольное осевое распределение интенсивности из лазерного пучка с гауссовым распределением интенсивности в сечении (рис. 1).

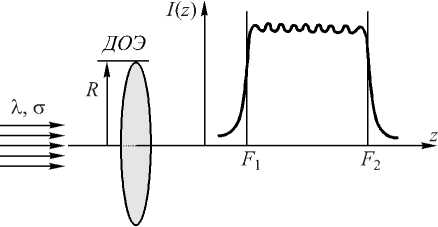
Рис. 1. Оптическая схема формирования продольного распределения интенсивности

Для расчета комплексной амплитуды F ( р , z ) на осевом расстоянии z и радиальном расстоянии р используем интеграл Френеля [20]

\ - ik I ik P2 I F(p,z)=---e explIx z V 2 z J

(    2 A

R I r 2 I x exp--- exp

J0     '^ „ 2 J

kr ²

i ф ( r ) + i "z^

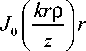
где R - радиус ДОЭ, J0 (x) - функция Бесселя первого рода нулевого порядка, ф (r) - фаза ДОЭ, а - радиус перетяжки освещающего гауссова пучка, к = 2л/Х - волновое число.

Запишем формулу для интенсивности на оптической оси

I (0, z ) = F (0, z )| 2, ik

F ( 0, z ) =--exp( ikz ) x z

/    2 A

^R I r ² I x exp--- exp

J 0     ¹       _o ² J

, x kr ²1 , i ^ф( r ) . 2 r d r .

Для формирования соосного отрезка представляется целесообразным выбрать в качестве минимизируемого функционала невязку:

N

^ф ( ф( r ) ) = El I ( ^z- )^- I ( ^z- ) • ^r- ,                 ⁽⁴⁾

i =1

где I (zi) - интенсивность, сформированная ДОЭ с фазовой функцией ф(r) на оптической оси на расстоянии zi, I (zi) - требуемый уровень интенсив- ности на оптической оси на расстоянии zi , рассчитанный из соображений закона сохранения энергии, N - число контролируемых точек на оптической оси, Cm - энергетический коэффициент, определяемый количеством уровней квантования m.

Для оценки оптимизируемого ДОЭ применялись два критерия: энергетическая эффективность и среднеквадратичное отклонение (СКО). Энергетическая эффективность рассчитывалась по следую- щей формуле:

INL     II N__I e=|EI(zi) I|EI (zi) I .

\ i =1        JV i=1

СКО рассчитывалось по формуле:

8 =

N ₂

E (I(z.)- I(z.))

i =1

N

E ।2 (zi)

i =1

2.    Выбор алгоритма оптимизации

Существует несколько подходов к организации оптимизации микрорельефа оптического элемента методами прямого поиска [21]. Прежде всего, это алгоритм полного перебора, когда производится поиск по всей области допустимых решений без каких-либо ограничений. Этот метод хорошо применим для плохо формализованных задач. Минусы его очевидны – это большие вычислительные затраты. Популярен также алгоритм имитации отжига [22], однако его особенности таковы, что по мере выполнения итераций все менее вероятным становится выход из локального минимума. Также существуют эволюционные алгоритмы, основанные на моделировании процесса естественной эволюции. В данной работе был использован генетический алгоритм, предложенный Джоном Холландом [23]. Этот алгоритм работает с группами решений, что является его отличительной особенностью и дает возможность выхода из локальных минимумов при разумных вычислительных затратах.

Принцип работы алгоритма заключается в создании начальной группы решений – популяции (родительского пула), состоящей из кодированных наборов параметров оптимизации задачи, называемых хромосомами, и применении к популяции хромосом генетических операторов. Наиболее популярные генетические операторы – это рекомбинация и мутация, которые увеличивают количество хромосом в популяции, и селекция, выбирающая по определенному принципу лучшие хромосомы. Основанием для оценки качества хромосомы служит значение функции приспособленности или функционала, подлежащего оптимизации. Ранее [24] было показано, что генетический алгоритм эффективен для решения задач подобного класса.

В данном исследовании была применена одноточечная и двухточечная рекомбинация (взаимоисключающие равновероятные) с вероятностью 85%. При этом точка (точки) среза выбиралась произвольно на протяжении всей длины хромосомы. Выбор хромосом для применения оператора рекомбинации был принят случайным, что обеспечило большую рассредоточенность направления оптимизации, тем самым снизив вероятность попадания в локальные минимумы.

Применялся стандартный оператор мутации с вероятностью 3% для каждого гена хромосомы, выбранной для применения данного оператора.

Оператор селекции требует более подробного рассмотрения в силу того, что существует множество стратегий селекции. Наиболее распространенная и простая в реализации – это элитарная селекция [21], приводящая к обеднению генетического материала популяции и, как следствие, к стагнированию алгоритма, попаданию в локальный минимум. Более предпочтительной для решения вышеобозначенной задачи выглядит турнирная селекция, которая заключается в случайном выборе нескольких хромосом в отдельную группу и анализе этих хромосом с точки зрения функции приспособленности. Такая стратегия, несмотря на несколько большую вычислительную нагрузку, обеспечивает высокую эффективность работы алгоритма, предотвращает вырождение генетического материала и, следовательно, снижает вероятность стагнации. В качестве дополнительного средства предотвращения стагнации среди хромосом группы с небольшой веро- ятностью (2%) в следующее поколение отбиралась хромосома, следующая за наилучшей.

Для оценки приспособленности хромосомы можно применить функционал (4), но, учитывая специфику данной задачи (в частности, снижение интенсивности излучения вдоль оптической оси по мере удаления от источника света), функционал был изменен:

N ф ( ф ( r ) ) = 2 i =1

exp

( ) - ¹

V ^{1 (} z ) Cm    J

аналитические представления фазовой функции. К таким можно отнести конический аксикон [10]. К преимуществам можно отнести простоту расчета фазовой функции ДОЭ, а к недостаткам - неизбежные погрешности квантования при использовании литографических технологий [25] и неравномерное распределение интенсивности вдоль оптической оси. Фазовая функция конического аксикона имеет вид:

Ф ⁽ r ) = mo^d 2n ^{( а} r ), ⁽⁸⁾

3.    Результаты численных экспериментов

В данной работе решалась задача оптимизации микрорельефа бинарного радиально-симметричного ДОЭ с радиусом R = 3,6 мм и количеством радиальных отсчетов M = 128, фокусирующего гауссовый пучок с параметрами λ = 1,06 мкм, σ =2 мм в десять равномерно распределенных фокусов на расстоянии от F 1 = 200 мм до F 2 =220 мм, составляющих высокоэнергетический световой отрезок.

Изменение значения функционала (7) с ходом итераций показано на рис. 2.

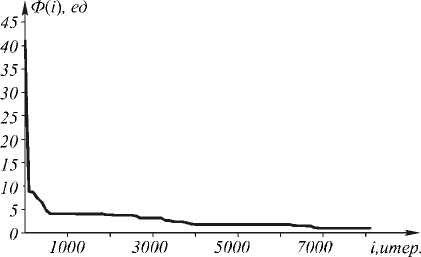
Рис. 2. Зависимость значения функционала от номера итерации

В процессе оптимизационной процедуры был получен микрорельеф ДОЭ, обеспечивающий следующие показатели качества распределения интенсивности, приведенной на рис. 3: е =4,58%, 8 =2,07%.

Вид радиального сечения рассчитанного бинарного фазового распределения приведен на рис. 4.

202   206  210  216   220 z, мм

Рис. 3. Распределение интенсивности вдоль оптической оси

4.    Сравнение полученных результатов с традиционными оптическими элементами

Для решения задачи фокусировки в продольный осевой отрезок также применяются ДОЭ, имеющие где а - параметр аксикона.

Рис. 4. Фаза бинарного ДОЭ, формирующего осевое распределение интенсивности

Известен также дифракционный аксикон [25], фазовая функция которого соответствует фазе бесселевой моды:

ф ( r ) = arg [ J 0 (^а r ) ] ,

где J ₀ ( r ) - Бессель функция первого рода нулевого порядка, а - масштабирующий множитель. Основное преимущество ДОЭ (9) – это бинарный профиль фазы, а недостаток такой же, как у конического аксикона – неравномерное распределение на осевом отрезке.

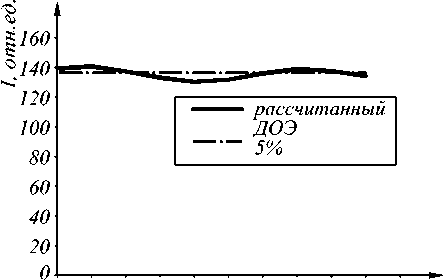
На рис. 5 приведено распределение интенсивности, сформированное коническим аксиконом (8) с параметром а = 30 и квантованной по двум уровням фазой; распределение интенсивности, сформированное дифракционным аксиконом (9) с масштабирующим множителем а = 30 (следует отметить, что фазовый профиль данного оптического элемента по определению является двухуровневым, принимая значения 0 или п , так что квантование не требуется); и распределение интенсивности, сформированное рассчитанным бинарным ДОЭ.

Из рис. 5 видно, что распределение интенсивности вдоль оптической оси, сформированное рассчитанным ДОЭ, является более энергетически выгодным, а также обеспечивает более равномерное распределение, чем распределения, сформированные другими оптическими элементами.

Заключение

Полученные результаты численного эксперимента позволяют сделать вывод об эффективности применения алгоритмов прямого поиска к задаче оптимизации квантованных оптических элементов, формирующих продольное распределение интенсивности. Сравнение с известными оптическими элементами, такими как бинарный вариант конического аксикона и дифракционный аксикон, показывает выгодное отличие рассчитанного в работе бинарного ДОЭ как по энергетической эффективности, так и по равномерности распре- деления. Также выгодное отличие стохастической дискретной оптимизации от прочих методов расчета в том, что решение ищется на пространстве технологически реализуемых решений, что делает поиск действительно прямым, исключая промежуточное кванто- вание. Отметим меньшую зависимость рассматриваемого подхода от параметров задачи, в отличие от аналитического расчета, где зачастую приемлемый результат достигается только для синтетического набора параметров, не реализуемого в технике.

О

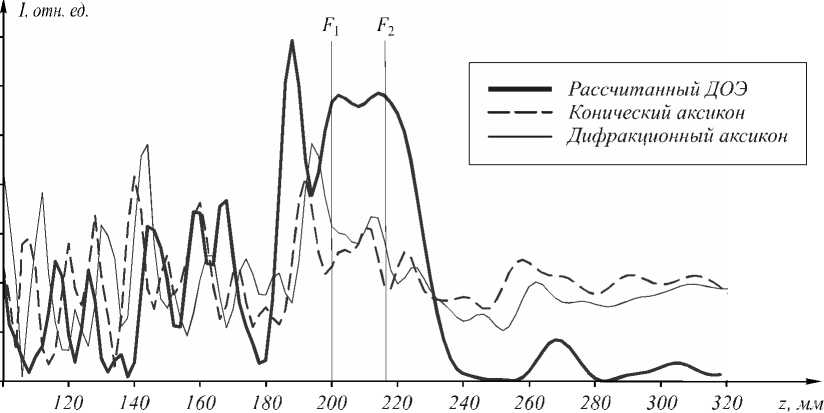
Рис. 5. Результат сравнения рассчитанного ДОЭ с известными аналогами