Оптимизация числа базовых станций в условиях сильно пересеченной местности

Обеспечение уверенной мобильной радиосвязи можно решить двумя способами:

• 1.    Поставить базовые станции большой мощности везде, где требуется обеспечить мобильную радиосвязь. Такое решение требует больших экономических затрат, повышенное использование частотного ресурса.

• 2.    Оптимизировать число базовых станций по их количеству, мощности, использованию частотного ресурса.

Для обеспечения уверенной мобильной радиосвязи с наименьшими экономическими затратами вопрос оптимизации числа базовых станций весьма актуален. В условиях сильно пересеченной местности задача оптимизации значительно усложняется, так как на область уверенного приема существенное влияние оказывает рельеф местности. На практике вопрос оптимизации числа базовых станций в условиях сильно пересеченной местности встречается, например, в горах, где ландшафт имеет ярко выраженную кривизну поверхности или в современных мегаполисах с домами повышенной этажности.

С математической точки зрения в общем случае мы имеем как минимум две поверхности, одной из которых является поверхность рельефа местности, а второй – воображаемая поверхность, образованная фронтом радиоволн, излучаемых антенной базовой станции. Эти две поверхности в некоторых областях, называемых областью уверенного приема, примыкают друг к другу (см. рис. 1). Очевидно, что при разумном размещении дополнительных базовых станций мы расширим область уверенного приема. На рис. 2 показаны эти же зоны уверенного приема, но в горизонтальной плоскости, причем радиус окружности соответствует зоне уверенного приема.

Исходя из этого, можно сделать следующее заключение. Если эти две поверхности имеют одинаковую кривизну на протяжении всего необходимого участка, то зона уверенного приема мобильной связи будет равна по протяженности всему участку, подлежащему установке мобильной связи, при условии, что метрика обеих поверхностей совпадает. При математическом исследовании кривизны поверхности определяется, что это условие часто не выполняется. Поэтому при выборе оптимального количества базовых станций с учетом кривизны поверхности необходимо учитывать метрику пространства.

Представление земной поверхности в виде математических уравнений

Сформулируем поставленную задачу с математической точки зрения. Предположим, что мы имеем сильно пересеченную местность, которую можно описать функцией:

w = f ( x , y ) . (1)

Этой функции можно поставить во взаимнооднозначное соответствие поверхность (ее график), погруженную в обычное евклидово пространство R³ с декартовыми координатами x , y , w . Соответственно в цилиндрических координатах r , ϕ , w поверхность будет описываться функцией w = f ( r , ф ) (см. рис. 3). Такой способ задания поверхности называют явным.

На поверхности можно вводить криволинейную сетку поверхностных координат. Например, lx, ly – поверхностные криволинейные координаты, которые получаются в результате сечения поверхности семейством вертикальных плоскостей WOX и WOY (см. рис. 3). Соответственно в цилиндрических координатах можно ввести криволинейные координаты lr, lφ, где lr – криволинейный радиус, получаемый с помощью сечения поверхности плоскостью WOR, а lϕ = r ϕ – дуга окружности. Задаваемые таким образом на поверхности криволинейные координаты являются в общем случае косоугольными (углы между координатными линиями на поверхности не всегда прямые, как в случае ортогональных координат).

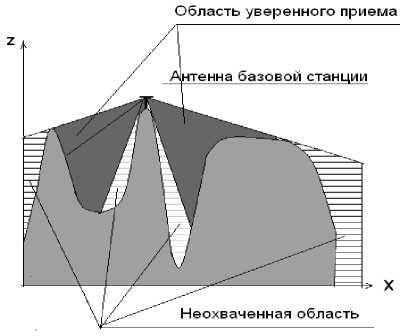
Рис. 1. Рельеф местности и области уверенного приема

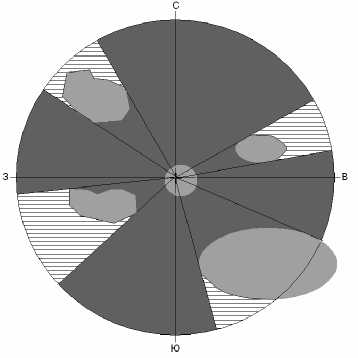
Рис. 2. Зоны уверенного приема (темно-серый цвет) и зоны, находящиеся в тени (недоступные зоны для связи – заштрихованные области)

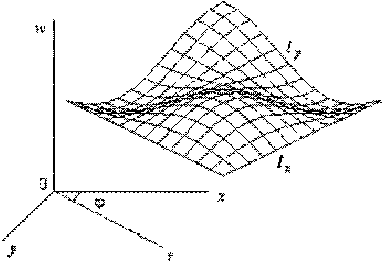
Рис. 3. График поверхности в декартовых координатах

Введем угол наклона касательной θ _x к кривой, получаемой сечением поверхности w = f ( x , y ) вертикальной плоскостью WOX, в текущей точке x (cм. рис. 4). Аналогично вводятся углы θ _y и θ _r для цилиндрической системы координат.

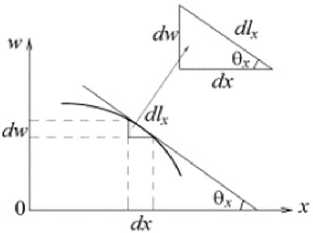
Рис. 4. Сечение WOX поверхности w = f ( x , y )

Напишем основные выражения, связывающие дифференциалы в декартовой системе координат dx , dy и в криволинейной системе координат dl_x , dl_y . Имеем в сечениях WOX (см. рис. 4):

то есть g ij = a jj , и в тензорных обозначениях первая квадратичная форма примет следующий вид:

I = dl ² = dr ² = d _y dy ⁱ dy ^J , g ij = g _ti . (6)

Первая квадратичная форма описывает поверхность в первом приближении, когда малый участок поверхности заменяется на участок касательной плоскости. Первая квадратичная форма определяет углы между линиями и длины дуг на поверхности, а также площади любых участков поверхности, то есть эта форма определяет метрику пространства.

Вернемся к кривизне поверхности – на этот раз с точки зрения геометрии Римана, которая использует тензорный анализ. Из литературы [3] известно, что главные кривизны находятся по формулам:

k _x

dl x 2 = dw ² + dx ² , dl _x

1+

dw ⎞²

I dx , dx ⎠

/1 .      '2

(1 + w x

w xx

11 + w'2 + w 2

k y

dx = dL cos 0, dw = dL sin 0; — = tgOv, x   x     xx      x dx

/1 .       '2

(1 + w y

w yy

I 1 + w x + w y

для сечений WOY:

dy = dl, cos O, ,. dw = dl, sin 9, ,,    (3)

y y      yy

dw

= tg @ .

dy

Соответствующие формулы верны и в цилиндрических координатах для сечения WOR. Мож-нотакжесказать,чтоформулы(3)задаютнеявно связьмеждудекартовымипеременнымиикри-волинейнымидлинаминаповерхности,вобщем случае x ( l x , l y ) , y ( l _x , l y ) , z ^{( l} _x , ^l y , ^O _x , ^O y ).

Согласно дифференциальной геометрии [2-3], можно определить метрический тензор, который в базисе {e i ^{( x )} }, (i = 1 , 2... n) имеет вид:

g

(x) _ ij

.( x)

r y ⁱ

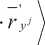
n