Оптимизация числа обслуживающего персонала на основе имитационного моделирования

Введение. Постановка задачи

Объектом исследования является отдел программного обеспечения фирмы, оказывающей аутсорсинговые услуги. Для исследования выбран процесс «Обслуживание клиента», модель которого представлена на рис. 1. В данный момент отдел программирования работает в очень интенсивном режиме. Это связано с тем, что число клиентов, а соответственно и число заявок на обслуживание, постоянно увеличивается. Таким образом, увеличивается и загрузка специалистов. График работ специалистов по внедрению составлен на 7-10 рабочих дней вперед. Необходимо определить оптимальное число специалистов для максимизации прибыли организации в целом.

Решение

Рассмотрим в качестве оперативной информации случайную величину Тр – время работы специалистов на выезде у клиентов (см. таблицу 1), а также информацию о времени между приходами заявок Т , полученную путем выборки из базы данных. Информацию о времени работы специалиста у клиента мы получаем из актов выполненных работ и реестров отработанного времени,а информацию о времени прихода заявки – из договора на обслуживание.

Преобразуем неупорядоченную совокупность полученных значений Тр по десяти интервалам и определим частоту попадания данной случайной величины в каждый интервал, среднее выборочное, дисперсию. В итоге получим следующие оценки – выборочное среднее: 4,435; дисперсия: 10,99; СКО: 3,315.

Эмпирическое распределение частостей Wj по выбранным десяти интервалам значений Тр представлено на гистограмме рис. 2.

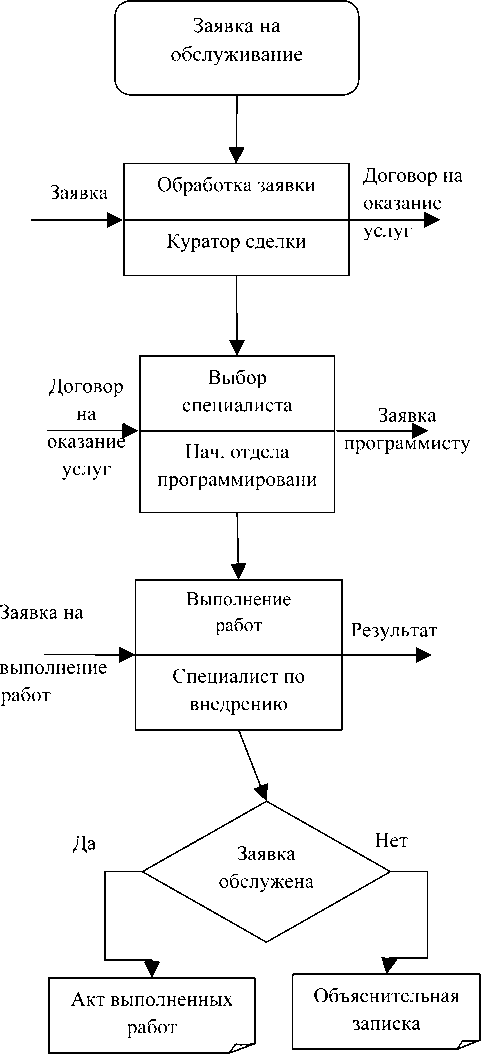
Рис. 1. Модель бизнес-процесса «Обслуживание клиента»

Вид гистограммы позволяет предположить, что исследуемая случайная величина подчиняется экспоненциальному закону распределения. Проверка этой статистической гипотезы по критерию z подтвердила это предположение.

Таблица 1. Время работы специалиста Tp
7,34	1,35	1,44	2,16	3,17	1,35
1,02	3,25	0,5	3,83	9,01	6,34
H,7	4,76	6,67	5,02	9,4	10,7
7,52	3,9	4,86	6,05	2,71	7,24
2,41	2,56	2,32	5,37	3,56	6,01
5,75	7,45	0,56	0,35	0,64	1,79
3,67	2,86	1,47	13,55	0,61	0,48
7,39	2,73	3,95	4,39	4,82	7,82
2,04	9,14	1,94	0,6	0,17	5,24
8,48	2,89	1,01	15,75	2,45	8,02
4,32	10,5	1,74	6,11	12	0,36
3,74	1,91	0,25	4,81	1,03	6,41
5,86	2,06	6,13

Нахождение наблюдаемого значения критерия . Зададим исходные данные: число степеней свободы 8; уровень значимости 0,05; критическое значение критерия согласия X ^kp = 15,5. По результатам вычислений получаем       =

3,067.

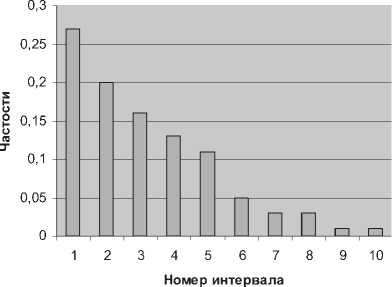
Рис. 2. Распределение трудозатрат времени на ис- полнение заявки специалистом

Так как Z Расч ^ X чь то нет оснований отвергать выдвинутую гипотезу о том, что распределение случайной величины т – времени работы у заказчика – соответствует экспоненциальному закону с параметром М. В качестве оценки параметра М показательного распределения применили величину, обратную выборочной средней м- VTcp.ehl6. Данная статистическая модель принимается, поскольку она согласуется с гипотезой о том, что генеральная совокупность полученных экспериментальным путем значений Тр распределена по экспоненциальному закону.

Аналогичным образом было установлено, что время между приходом заявок Т, также подчинено экспоненциальному закону с параметром л = 0,073.

Информация для проведения имитационного моделирования проверена и готова к исследованию в модельных экспериментах.

Модуль имитационного моделирования, оперируя входящими данными, вычисляет оптимальное количество специалистов, работающих на выездах у клиентов, высчитывает совокупную прибыль от их работы и наглядно иллюстрирует связь количества специалистов с прибылью от их работы.

В соответствии с изложенным входными параметрами имитационной модели (ИМ) выбираются: число специалистов N_k (существующее в настоящий момент), среднее время между двумя заявками 7 , среднее время обслуживания заказа Pobsl , период работы системы , число случайных реализаций R .

Выходными характеристиками модели являются: среднее число обслуженных заявок N₀^_si, оптимальное число специалистов N_m и средняя относительная прибыль ( C _ср.отн.).

После определения входных параметров и выходных характеристик необходимо выбрать показатель и критерий эффективности ИМ рассматриваемого процесса.

В качестве показателя эффективности целесообразно выбрать среднюю прибыль, определяемую по формуле: C_cp=_PN_obsl-z(N_kY где р – чистая прибыль, полученная в результате обслуживания одной заявки; Z^N^ - издержки обслуживания всех заявок, зависящие от числа каналов. Разделив обе части данного равенства на величину Р , получим следующее выражение для расчета показателей эффективности:

Ccp.om„.=Nobsl-Z(NkP Pt где ср.о – средняя относительная прибыль.

Величину ^z^N_kM p (отношение общих издержек обслуживания к чистой прибыли, полученной в результате обслуживания одной заявки)

можно рассматривать как функцию числа каналов.

Примем в качестве конкретной зависимости издержек обслуживания от числа каналов следующую функцию:

z(Nk)/p = l-0,5Nk+0,5(Nky.

Таким образом, для расчета показателя эффективности будем использовать зависимость

В качестве критерия выбора наиболее выгодной структуры СМО примем оптимальное число каналов, обеспечивающее максимум средней относительной прибыли:

K(N_opl) : MAXVC„,(N_k)\;N_k = 1 ...15.

Теперь необходимо спроектировать моделирующий алгоритм. Исходными данными будут являться: фактическое число специалистов по внедрению ( N_k ); среднее время между приходами заказов ( T _cp); среднее время обслуживания заказов ( T _obsl); число случайных реализаций ( R ); максимальное число заказов ( N _zmax); прибыль от заказа ( C _cp). В результате получим число обслуженных заказов ( N _obsl); среднее возможное время поступления заказов ( T _cp); среднее возможное время обслуживания.

Выходными характеристиками модели являются число обслуженных заказов ( N _obsl) и показатель эффективности ( C _cp.отн.), которые позволяют по полученным результатам моделирования построить диаграммы распределения средней относительной прибыли в зависимости от числа специалистов. Рассмотрим более подробно алгоритм модели с оптимизацией числа специалистов (см. рис. 3).

Блок 1 представленного на рис. 3 алгоритма проводит обнуление переменной GN_obsi – суммарного значения обслуженных заявок. С блока 2 начинается циклический перебор случайных реализаций, число которых задается пользователем.

В блоке 3 в начале каждой реализации производится обнуление локальных переменных: число заявок N _ , поступающих в одной реализации; число обслуженных заявок в каждом из каналов ^obs!* начальные значения времени освобождения каналов -^Ao/ . В блоке 4 имитируется поступление заявки на обслуживание.

Блок 5 является началом цикла обслуживания заявок. Блоки 6-9 производят выбор канала, ко- торый характеризуется наименьшим значением времени обслуживания заявки.

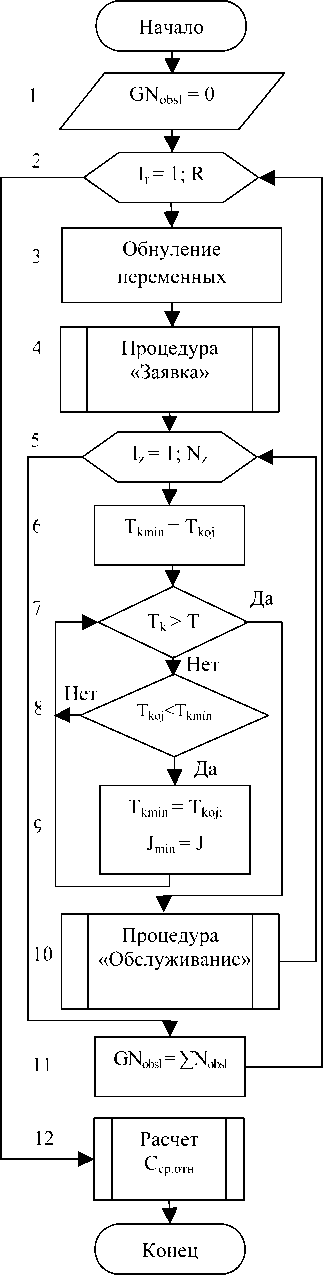
Рис. 3. Алгоритм модели

Блок 10 обращается к процедуре обслуживания очередной заявки.На выходе этой процедуры заявка

находится в выбранном канале ^obs! (^min ) .Блок 11 служит для расчета суммарного числа обработанных заявок по рекурсивной формуле: . Блок 12рассчитывает значение выходной переменной – средней относительной прибыли ( C _ср.отн.).

Автономные алгоритмы формирования потоков заявок и обслуживания заявок имитируют работу по формированию потоков поступления и обработки заявок с использованием датчика случайных чисел ДСЧ ( а ), который вырабатывает возможное значение случайной величины а ,равномерно распределенной на интервале [0; 1).

На рис. 4 представлен алгоритм формирования потоков заявок.

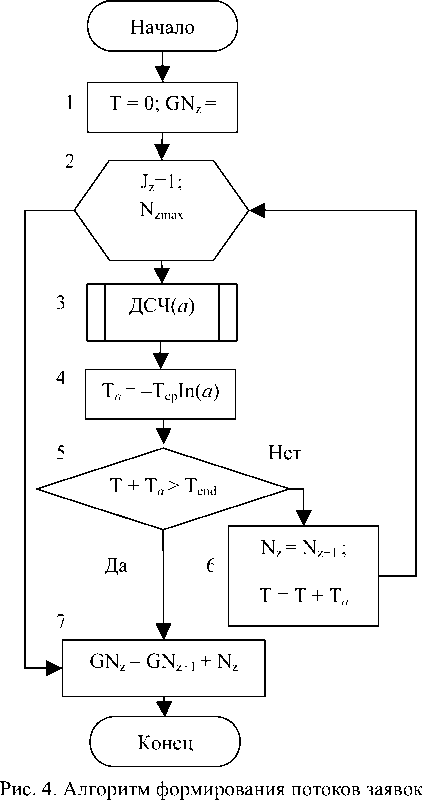
Блок 1 здесь производит обнуление модельного времени T ; блок 2является началом цикла формирования заявок. Блок 3 и 4 формируют значения случайного времени поступления очередной заяв-ки.При этом блок 3 обращается к датчику случайных чисел ДСЧ ( а ), который вырабатывает возможное значение случайной величины а , равномерно распределенной на интервале [0; 1).

В блоке 4 определяется возможное значение моделируемой случайной величины при условии, что среднее время между поступившими заявками равно ^Te_P .Блок 6 подсчитывает число поступивших заявок, помещает время поступления каждой заявки в специальный массив и изменяет модельное время T . Блок 5 проверяет условие окончания процесса формирования заявок.Алгоритм формирования потоков обслуживания заявок аналогичен алгоритму формирования потоков заявок. Модуль имитационного моделирования представляет собой форму с несколькими вкладками.

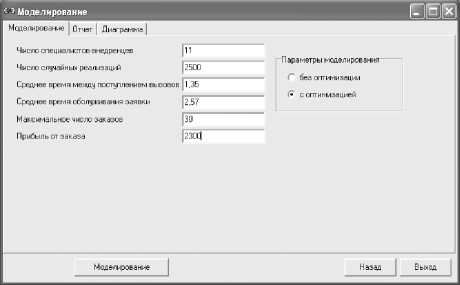
Рис.5.Интерфейс модуля моделирования (ввод данных)

На вкладке «Моделирование» (см. рис. 5) задаются исходные данные и параметры моделирования. На вкладке «Отчет» выводятся результаты моделирования: количество обслуженных заявок, оптимальное число специалистов, значение показателя эффективности – средней прибыли. На вкладке «Диаграмма» производится построение диаграммы, иллюстрирующей зависимость показателя эффективности работы исследуемого объекта от числа работающих специалистов.

Рассмотрим контрольную задачу, заданную набором входящих данных (таблица 2) и проанализируем полученные конкретные результаты с точки зрения их соответствия заложенной в модель общей схеме решения.

Таблица 2. Показатели, необходимые для проведения имитационного моделирования

Наименование показателя	Значение
Фактическое число специалистов	11
Число случайных реализаций	200
Среднее время между поступлением вызовов	1,53
Среднее время обслуживания заявки	2,57
Максимальное число заявок на обслуживание	30
Прибыль от заказа, руб.	1600

Результаты решения тестовой задачи представлены в виде таблицы 3. Для обеспечения приемлемой достоверности результатов ИМ число случайных реализаций было выбрано равным 200.

Таблица 3. Результаты имитационного моделирования

Наименование показателя	Значение
Число обслуженных вызовов	138
Среднее число обслуженных заказов одним специалистом	12,5
Оптимальное число специалистов	13

На рис. 6 представлена диаграмма распределения средней прибыли предприятия в зависимости от числа специалистов по внедрению, полученная с помощью метода имитационного моделирования и на основе приведенных в таблице 2 тестовых исходных данных.

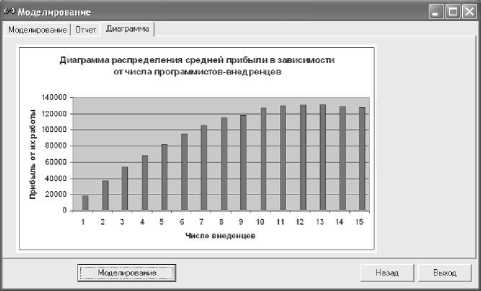
Рис. 6. Интерфейс модуля ИМ

Диаграмма на рис. 6 иллюстрирует оптимальное число специалистов: N_m = 13. При этом прибыль (при условии стоимости одного вызова 1600 руб.) будет равна 131750 руб. Также на диаграмме показан характер изменения прибыли при числе специалистов по внедрению N_m = 1...15.

Выводы

По результатам проведения ИМ с определенными входными параметрами можно сделать вывод о том, что для эффективной работы подразделения необходимо увеличить число специалистов по внедрению на 2 единицы. Связанное с этим увеличение фонда заработной платы будет покрываться за счет выполнения большего числа заказов на сопровождение программных продуктов.

Следовательно, руководству фирмы целесообразно рассмотреть возможность увеличения штата сотрудников.