Оптимизация динамики автоматизированного электропривода с разрывным управлением

Разработка и совершенствование методов и алгоритмов синтеза управления сложными динамическими объектами, описываемыми системой дифференциальных уравнений высокого порядка, коэффициенты которых могут меняться в широком диапазоне, является актуальной проблемой современной теории и практики управления [1]. Примерами подобных объектов могут быть различные летательные аппараты, манипуляционные и мобильные роботы, станки, экскаваторы, различные технологические установки и процессы.

Эти объекты представляют собой сложные многомассовые системы, на динамику которых большое влияние оказывают зазоры в передачах и действие упругих элементов, причем жесткость упругой связи и момент инерции исполнительного органа значительно меняются в процессе технологического цикла и зависят от геометрического положения исполнительного органа в пространстве. В данной статье в качестве такого органа рассмотрен электропривод копающего механизма экскаватора.

Одним из перспективных подходов к синтезу систем управления сложными динамическими объектами является применение систем с переменной структурой (СПС), разработанных академиком С. В. Емельяновым и его школой [2]. Наиболее широкое распространение в этом подходе получило направление, изучающее скользящие режимы [3]. В таких режимах движение изображающей точки определяется уравнением поверхности переключения и не зависит от свойств объекта управления, т. е. система, находящаяся в скользящем режиме, инвариантна к параметрическим и внешним возмущениям.

Управление автоматизированными электроприводами, питающимися от силовых управляемых полупроводниковых преобразователей энергии, осуществляется изменением напряжения. Современные силовые приборы работают преимущественно в ключевом режиме с целью обеспечения малых потерь энергии. Следовательно, управляемый электропривод является динамической нелинейной системой, описываемой дифференциальными уравнениями с разрывной правой частью.

Напряжение, подаваемое на обмотку электрической машины и являющееся для нее управлением, в силу ключевого характера работы полупроводниковых элементов преобразователя напряжения, носит разрывной характер. В этом случае разрывной характер управления, являющийся основным признаком систем с переменной структурой, не является навязанным системе извне свойством, а определяется ее физической природой, что и обусловливает перспективность использования скользящих режимов для управления электроприводами.

Математическое описание двухмассовой электромеханической системы (ЭМС) с силовым полупроводниковым преобразователем при общепринятых допущениях может быть представлено системой линейных дифференциальных уравнений [4]:

X = A X + B u , (1)

где X = [ i_a и , M у ю ₂ J T - вектор состояния системы, здесь i a - ток якорной цепи, « | - скорость первой массы, M y - упругий момент, ю ₂ - скорость второй массы; u – управляющее воздействие; A – 4 × 4-мерная матрица; B – вектор размера 4 × 1.

Математическое описание системы при исследовании ее динамики дается в относительных единицах, т. е. координаты электропривода рассматриваются относительно их базовых значений. В качестве базовых для напряжения управления и угловых скоростей приняты их номинальные значения, для тока якорной цепи и момента – их максимальные (стопорные) значения.

Сведем задачу управления к задаче стабилизации. Для этого введем вектор желаемого состояния X ж для двухмассовой системы:

T                     iT ia ж ®1ж Mу ж ®2ж J = [0 g 0 g ] ,

Хж = [0 1 0 1]Tg = Lg , где (*ж , ю*ж, MУж, ®2ж - желаемые значения в установившемся режиме для тока якорной цепи, скорости первой массы, упругого момента и скорости второй массы в относительных единицах соответственно; g – задающий сигнал. Необходимо синтезировать такую функцию управления u с использованием информации о векторах состояния объекта X и вектора желаемых величин Xж, чтобы вектор рассогласования E = Xж – X был сведен к нулю.

Запишем уравнение движения относительно вектора рассогласования с учетом того, что Х _ж = 0:

E = A E - B u - K g ,            (2)

где K = AL .

Таким образом, будем рассматривать K g как возмущающее воздействие. В работе [1] доказано, что его влияние на динамику системы можно устранить с помощью разрывного управления.

Как известно, уравнение поверхности переключения имеет вид s = CE = 0,                 (3)

где C – вектор коэффициентов поверхности переключения размера 1 × 4.

Для приведения системы (1) к регуляторной форме [3] введем пространство новых переменных, связанных с исходными линейным преобразованием

E = ME, чтобы для рассматриваемой двухмассовой системы четвертого порядка выполнялось условие

MB = [ 0 0 0 1f.             (4)

Для этого первые три строки матрицы M должны быть составлены из базиса трехмерного подпространства, ортогонального управлению:

	■ 0	0	0	1
	0	0	1	0
M =	0	1	0	0
	. 1/ b	0	0	0

Поведение системы (2) в пространстве новых переменных E описывается уравнением

— = MAM-1E - MBu - MKg, dt или

—¹ = ^A 11 ^E 1 + A 12 e 4 - ^K 1 g ,

< dt de

,4 = A 21 E 1 + a 44 e 4 ^- u ^- k 2 g , I dt

где E ₁ и e ₄ – соответственно четырех- и одномерный векторы состояния, полученные из компонентов вектора e' :

f E . )             Т

^E = 1 _ I , ^E 1 = ( ^e 1 e 2 e 3 ) ,

I e 4 J

( A A A

MAM ^{- 1} =1 ¹¹     1 ² I , MK = 1 ,

( ^A 21 ^a 44 J         ( ^k 4

K 1 = ( k ‘ k 2 k 3 ) ^T .

При синтезе поверхности переключения пренебрегаем возмущающим воздействием, влияние которого в дальнейшем скомпенсируем выбором соответствующего разрывного управления.

Уравнение (3) поверхности разрыва s = 0 относительно новых переменных имеет вид

5 = CM ^{- 1} E = C 1 E 1 + c 4 e 4 4 = 0,         (6)

где CM ¹ = ( C 1 c ₄ ) ; C 1 = ( c 1 c ₂ c 3 ) . Для простоты синтеза примем с 4 = 1.

Для получения уравнения движения в скользящем режиме с учетом (5) необходимо решить уравнение 5 = 0 и подставить полученное решение в систему (6):

—¹ = A 11 E 1 + A 12 e 4 - K 1 g , dt

. e 4 =- C 1 E 1 .

Систему (7) можно рассматривать как разомкнутую систему с вектором состояния E ₁ , управлением e ₄ и возмущением g . Таким образом, нахождение поверхности скольжения сводится к задаче оптимального управления первым уравнением системы (7).

Для оптимизации движения системы (7) в скользящем режиме классический критерий оптимальности вида

J = j( ET QE + ru 2)dt не годится, так как движение в скользящем режиме не зависит от управления и определяется положением поверхностей разрыва. Поэтому в качестве критерия нужно рассматривать функционал

J = J ( E Т QE ) dt ,             (8)

где Q – весовая диагональная матрица.

Оптимизируемый функционал (8) относительно новых переменных приобретет вид

J

J = J ( E 1 Т Q 11 E 1 + 2 Ё 1 Т Q 12 e 4 + q 44 ( e 4 ) ² ) dt ,     (9)

гл/г-1 \Т      —1  I ^11 ^12 IглТ где (М ) QM = I           I; Q21 = Q12 .

V Q 21 q 44 )

Для рассматриваемой электромеханической системы

Q 11

q ₄₄ 0

Q21 =[0 0  0], q44 = [qnb2 ] , т. е. векторы Q12 и Q21 являются нулевыми. Тогда

J = J ( E 1 ^T Q 11 E 1 + q 44 e ₄ ² ) dt .             (10)

Выбирая E ₁ в качестве вектора состояния, а e ₄ – в качестве управления для движения в скользящем режиме, получим классическую постановку задачи оптимального управления с квадратичным критерием [5]. Иными словами, оптимальное управление системой (7) при критерии (10) определяется следующим образом:

e4 = - q 44-X PE1, где Р – решение матричного уравнения Риккати:

PA_n + А 1 Т P - PA 12 q 44X2 P + Q_n = 0.

Таким образом, оптимальное управления e4 из (7) имеет вид e4 = -C1E1 =- q4-1АТ2РЕ1.

Из последнего выражения имеем C 1 = q 441 А Т 2 Р , подставив которое в (6), получим уравнение поверхности переключения (в исходных координатах), на которой должен быть организован скользящий режим:

5 = CM ^{- 1} E = CM ^{- 1} ME = [ C 1 c 4 ] Me =

= [ q ^P 1] ME = 0..

При организации управляющего воздействия в виде кусочно-линейной функции вектора желаемого состояния системы и вектора рассогласования

I         nI u=IaEel-qg Isign(5)

V i=1

в системе возникнет устойчивый скользящий режим на выбранной поверхности переключения.

Из теории систем с переменной структурой известно, что для обеспечения устойчивого скользящего режима на поверхности s необходимым и достаточным условием является выполнение неравенства

55 <  0 .

Производную поверхности переключения можно записать в виде

5 = HE - du - pg = 0 ,

где H = CA ; d = CB ; p = CK . Подставим значение 5 из (13) с учетом управления (11) в условие (12):

I I -ni 11II

5 1 HE - d I a^ | e |- q|g | I sign( 5 ) - pg I < 0.

Условие устойчивости выполняется, если выполняется следующая система неравенств:

I1

5 HE - d a^ e sign( 5 ) <  0,

V)

5 ( ^- pg ⁺ dq\g\ sigⁿ⁽ 5 ) ) <  0.

Таким образом, скользящий режим устойчив при соблюдении условия da > max (|hi |), dq <-| p|.

При выполнении этих неравенств в законе управления (11) на поверхности s = 0 всегда возникает скользящий режим.

В рассмотренном выше алгоритме все компоненты управления (11) пропорциональны норме вектора желаемого состояния и вектора рассогласования с одними и теми же коэффициентами a и q , которые должны удовлетворять условию (14).

Графически работа системы управления с переменной структурой может быть представлена следующим образом (рис. 1).

В результате исследования влияния весовых коэффициентов критерия оптимальности на динамику электромеханической системы были определены следующие рекомендации по выбору этих коэффициентов.

Необходимо, чтобы все коэффициенты весовой диагональной матрицы были больше нуля, и при расчете в относительных единицах эти коэффициенты удобно вначале поставить равными единице.

Весовые коэффициенты нужно подбирать одинаковыми для пар координат: первая пара – рассогласования скоростей первой и второй массы; вторая пара – рассогласования тока якорной цепи и упругого мо- мента. Коэффициенты в каждой группе координат нужно принимать равными по значению и в процессе настройки требуемого качества регулирования изменять одновременно на одну величину. Это заметно упрощает процедуру выбора весовой матрицы. При этом расчет в относительных единицах позволяет использовать тот факт, что равные по значению весовые коэффициенты при координатах означают равный вкладываемый вес или равную важность минимизации этих координат между собой.

Коэффициенты при рассогласованиях скоростей следует выбирать больше единицы, так как в этом случае увеличивается быстродействие системы и ток рекуперации при стопорении, что позволяет снизить амплитуду упругого момента. Однако чрезмерное их увеличение ведет к повышению колебательности системы и может вызвать незатухающие автоколебания скорости и тока.

Влияние весовых коэффициентов критерия оптимальности на показатели динамики ЭМС показано на представленных ниже графиках (рис. 2–5).

Снижение коэффициентов при рассогласованиях тока якорной цепи и упругого момента усиливает эффект от повышения коэффициентов при рассогласовании скоростей. Поэтому большое значение имеет отношение коэффициентов при скоростях и моментах.

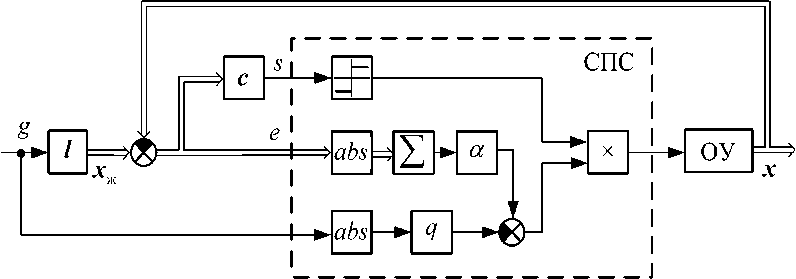
Рис. 1. Алгоритмическая схема системы с переменной структурой

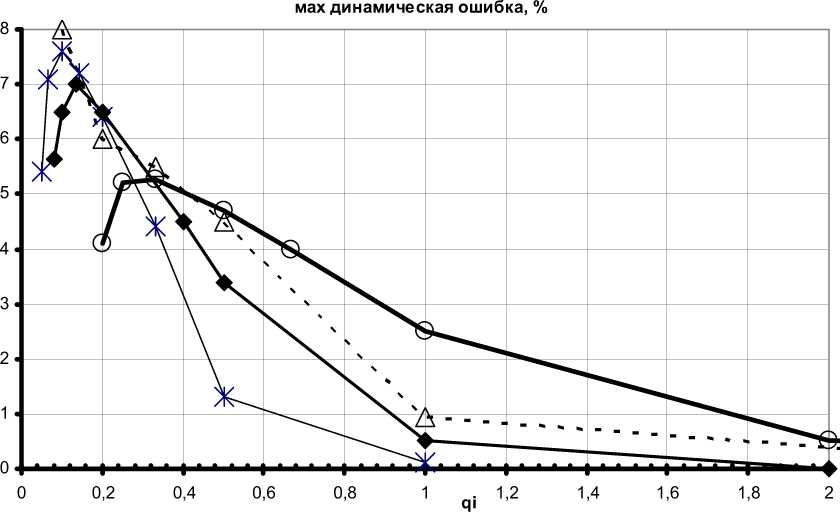
qw=1       qw=2       qw=5       qw =10

Рис. 2. Зависимость максимального перерегулирования скорости второй массы от весовых коэффициентов при i_a и M _у и различных весовых коэффициентов при ω

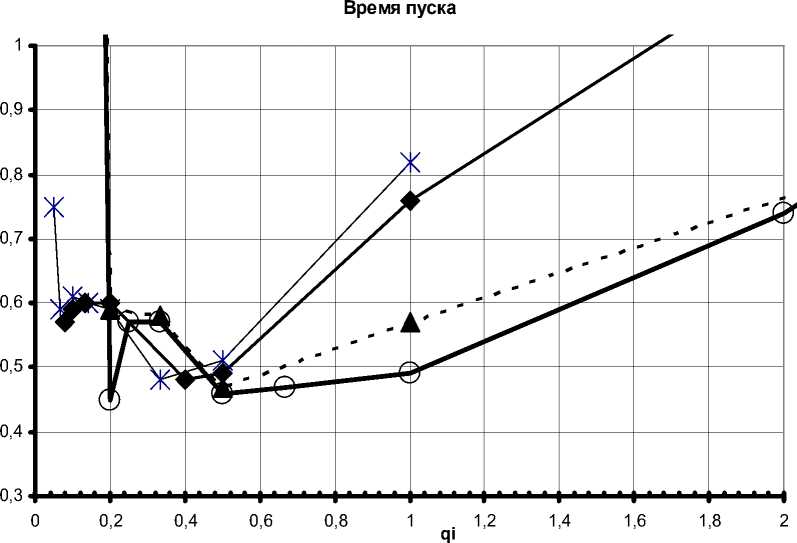
-ж qw =1 ---•   qw =2 - -▲ qw =5        qw =10

Рис. 3. Зависимость времени переходного процесса скорости второй массы от весовых коэффициентов при i_a и M _у и различных весовых коэффициентов при ω

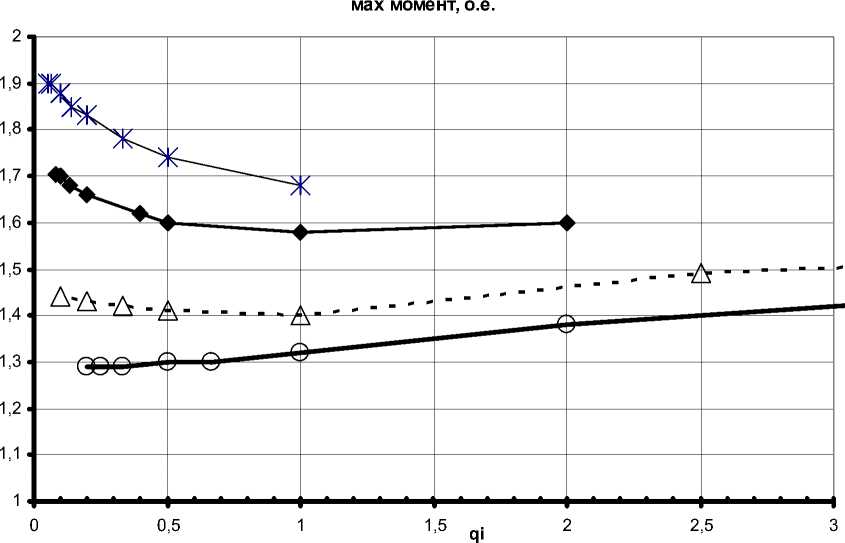
■* qw=1       qw=2 - - △ - - qw =5 ^^ qw =10

Рис. 4. Зависимость максимального упругого момента от весовых коэффициентов при i_a и M _у и различных весовых коэффициентов при ω

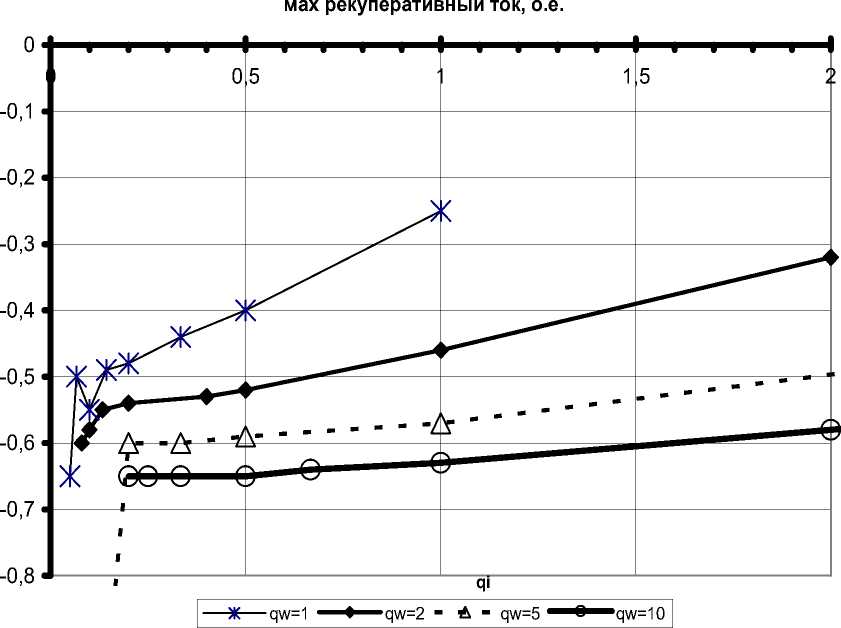
Рис. 5. Зависимость максимального рекуперативного тока при стопорении от весовых коэффициентов при i_a и M _у и различных весовых коэффициентов при ω

Таким образом, весовые коэффициенты при рассогласовании i a и M у следует выбирать меньше 1, а весовые коэффициенты при рассогласовании скоростей – больше в 20–25 раз коэффициентов при рассогласовании i_a и M _у.

Итак, авторами решена задача динамической оптимизации ЭМС при помощи скользящих режимов. Результаты моделирования показали работоспособность и устойчивость синтезированной системы управления к внешним возмущающим воздействиям.