Оптимизация движения космического аппарата с двигателем малой тяги в системе Земля-Луна

Самарский государственный аэрокосмический университет

Описывается оптимизация законов управления и траекторий движения космического аппарата с двигателем малой тяги, выполняющего транспортные задачи в системе “Земля - Луна”. С использованием формализма принципа максимума Понтрягина получены необходимые условия оптимальности управления с точки зрения быстродействия. Движение рассматривается в рамках плоской круговой ограниченной задачи трех тел. Получены решения для задач оптимального по быстродействию достижения устойчивых точек либрации системы и пролета Луны на требуемом угловом расстоянии. Предложен подход к выбору начальных параметров краевых задач.

Движение космических аппаратов (КА) в системе Земля–Луна традиционно рассчитывалось в рамках теории сфер действия. Это оправдано при использовании двигателей большой тяги в рамках импульсной постановки баллистических задач. Однако, при расчете движения в системе Земля-Луна КА с малой тягой, реактивное ускорение от двигательной системы сравнимо с возмущающими ускорениями Земли и Луны. В таких условиях некорректно полагать, что оптимальное управление не зависит от гравитационных воздействий второго притягивающего центра. В данной работе рассматривается проблема оптимального с точки зрения быстродействия управления и соответствующих ему траекторий движения в рамках плоской круговой ограниченной задачи трех тел.

Рассматривается движение КА с электро-реактивной двигательной установкой (ЭРДУ) под действием гравитационных сил притяжения Земли и Луны. Считается, что орбиты Земли и Луны относительно барицентра системы – круговые, возмущения от нецентральности гравитационного поля притяжения Земли и других небесных тел не учитываются. Возмущения, связанные с работой двигательной установки, например падение мощности при воздействии радиационных поясов Земли или ограничения на управление, связанные с особенностями углового движения КА в данной работе не учитываются.

Математическая модель движения и оптимальное по быстродействию управление Движение аппарата описывается в инерциальной полярной барицентрической системе координат (рис. 1). Основная плоскость совмещена со средней плоскостью движения Луны, полярная ось направлена в этой плоскости в сторону точки весеннего равноденствия, центр координат находится в центре тяжести системы Земля - Луна. Положение центра масс КА относительно барицентра определяется радиус-вектором r и полярным углом ϕ. Расстояние от КА до Земли и Луны соответственно задается векторами rЗ и rЛ . Вектор реактивного ускорения от тяги двигателей лежит в основной плоскости, его величина зависит только от массы КА. Направление ускорения задается углом управления л(t), который отсчитывается от радиус-вектора против часовой стрелки. Положение Земли и Луны определяется постоянными по величине радиус-векторами RЗ и RЛ и углом ϑ , имеющим постоянную скорость изменения щ равную средней угловой скорости движения Луны по орбите.

Все фазовые координаты системы приводятся к безразмерному виду. Для этого все линейные расстояния относятся к среднему

Рис. 1 . Инерциальная полярная барицентрическая система координат

d ( A y ) _ V y dt r

- to .

В этих обозначениях расстояния от КА до Земли и Луны равны соответственно:

r₃ _ д/ r ² + R ^ + 2 rR_З cos ( A y ) ,

^г л ^_ 4r ^{2 +} R ^ ^{- 2 rR}л ^{cos ( а} У ) .     ⁽²⁾

В качестве критерия оптимальности будем использовать минимальную длительность выполнения целевой задачи:

расстоянию от Луны до барицентра R_Л , время к среднему периоду обращения Луны, ускорение к гравитационному ускорению на орбите Луны. В этом случае уравнения движения имеют вид:

T

T _ J dt ^ min

Введем вектор фазовых координат КА

X _ ( r, A y, V_r, V _y , m ) T . Формально за-

dr _ v      dy _ V^

dt ^r , dt " r ’

dV r dt

V^{2         r} + R ^{cos (} y - 9 ) Ц л ^{( r - R} Л ^{cos (} y - 5 ))

(1 - Цл )----------3---3------------+ a, r                      rЗ3                       rЛ3

dV ϕ dt

^VV y            ^R 3 Sin ⁽ y - ⁹ ) ц ^R sin ⁽ y - ⁹ )

------^{+ (1} - ^Ц л ) --------3---3--------- ⁺ a.

r                         r З ³                      r Л ³

a

r

a 0 δ

( 1 - m )

d m a ₀ δ dt c ^,

cos λ

a ϕ

a 0 δ

( 1 - m )

sin λ

Здесь V_r , V _ϕ – компоненты безразмерного вектора скорости КА относительно барицентра; м_Л ? 0.0123 – отношение массы Луны к суммарной массе системы Земля-Луна; a ₀ – номинальное безразмерное ускорение от тяги двигателей; с – безразмерная скорость истечения рабочего тела; д – функция вклю-

дача оптимизации описывается следующим образом: требуется определить вектор функций управления u ( t ) _ ( z ( t ) ,A ( t )) ^T из допустимого множества U , удовлетворяющий граничным условиям X ( 1 0 ) = X 0 , X ( T ) _ X K и доставляющий минимум критерию оптимальности T при фиксированном векторе проектных параметрах p _ { a 0 , c } T :

u opt ( t ) _ argminT ( й|р _ fixe,X о _ fixe,X к _ fixe ) U ( t ) .

В соответствии с формализмом принципа максимума Понтрягина введем вектор сопряженных переменных P _ ( P r , P _y , P V , P V_v , P_m ) T

и Гамильтониан H ^_

< dX ) T

I dt )

• P

.

mРТ чения-выключения двигателей; m _     - m0

относительный расход рабочего тела.

Заменим в уравнениях (1) угол ц на угол Луна - барицентр - КА по формуле A y _ y - 9 . Дифференциальное уравнение, описывающее изменение этого угла, примет вид:

Из условия максимума Гамильтониана определим оптимальное направление вектора ускорения X_opt ( t ) и функции включения-выключения двигателей:

sinλopt

cosλopt

P

V _ϕ

2 + P ²

V _ϕ

P

r

2            2 ,

+ 1 V rϕ

где

5 =^

[ 0 ,

1 ,

А< 0

А> 0,

^PV _r

Л _о — arctg--- □ _ р ² , р ² р р ⁰         Р , B ^— Р ^Р У г ^{+ Р}Уф , ^Рт , ^{Р д} ф ,

V _ϕ

/ „ 9    „ 9

Р А Ру + Ру А — _т + \----у_ c 1 — т

.

Система сопряженных уравнений для этой задачи имеет вид:

dP _{— Р} dt ^{V r}

V- ф² . ¹ . Д л ^{3 ( 1 —} Д л X ^{r + R} 3 cos ^А Ф ^{)2 +} Т ⁺ Т

r    r _З    r _Л

r З ⁵

—

—

3 д _л ( г — R _Л cos А ф ) ² r Л ⁵

V ^ϕ + ϕ ₂ +

( Р_г — ± 1 - из условия нормировки), чтобы на концах оптимальной траектории выполнялись начальное и конечное условия X ( t 0 ) — X 0, X ( т ) — X_T .

Пусть стартовая орбита круговая, радиусом r ₀ , и положение КА относительно Луны в начальный момент А ф ₀, в этом случае начальный вектор фазовых координат задается значениями

P

V _ϕ

—

V r V ₊ r ²

3 - 3 ( 1 — ц_Л ) sin А ф ( г + R₃ cos А ф )

⁵ r_З

—

—

3 Д Л — Л sin А ф ( г — —_Л cos А ф )

r Л ⁵

,

аР А ф dt

r

- PVr —(1 — Дл )

V

R₃ sin А ф --3— ⁺ + r_З

Г r.                       RT )

X 0 — 1-^ , А ф о , V r 0 — 0 , У ф о — -Л -1 .(8)

V ^- Л                                r ^Г 0 У

В зависимости от цели перелета конечные значения вектора фазовых координат задаются следующим образом:

1) для задачи достижения устойчивых точек либрации системы

3 ( 1 — д _л ) rR. sin А ф ( r + R₃ cos А ф )

+----------------5---------------+ rЗ

T

X t — | 1 , А ф к — ± -3- , У_д — 0 , У ф_к — 1 1 ;(9)

ц _Л—_Л sin А ф З ц _л г— _л sin А ф ( г — —_Л cos А ф р ---------- — ------------------------

2) для пролета Луны на заданном угло-

+3 r Л ³

⁵ r_Л

–

У

вом расстоянии А ф_к с не фиксированным

+

P V _ϕ

R₃ cos А ф

г ³

V r

—

Д л ^- л ^{cos А} ф г ³ r_Л

3 — 3 rsin ² А ф + 3д_ЛR Л _Лrsin ² А ф

⁵ r_З

⁵ r_Л

X

вектором скорости V_T — ( v r _T, У _{ф Т} ) ^т , с учетом условий трансверсальности для вектора скорости

X t — ( 1 , А ф_к, Р у — 0 , Р у _ф — о)" . (10)

У

dP r dt

—

Р + Ру r     Vϕ

V ϕ

^, r

dP _m

Так как —^7 ^ ⁰ , при всех t е [ t ₀ , Т ] , и

аРУф = РфУ — 2 Рууф — Р Аф dt              r dPm      a0δ     2    2

at    (1 - m ) ² PV ^{+ Р}' ^ф .

Таким образом, задача об оптимальном по быстродействию плоском движении в системе “Земля-Луна” сводится к следующей двухточечной четырехпараметрической краевой задаче. Требуется найти такие начальные значения

для задачи на оптимальное быстродействие расход рабочего тела в конечный момент времени не фиксирован, то, согласно условиям трансверсальности, Р_т ( Т ) — 0 . При t е [ 0 , Т ) Р_т ( t ) >  0 , поэтому для задачи на оптимальное быстродействие функция включения-выключения двигателей, согласно (6) 5 ( t ) = 1, то есть двигатель работает без выключений. Кроме того, в силу монотонного убывания функции Р_т ( t ) удобно использовать эту со-

пряженную переменную для выхода из ин-

тегрирования. Остальные сопряженные переменные и фазовые координаты могут изменяться немонотонно, а длительность перелета неизвестна.

Численные методы, применяемые при решении

Моделирование оптимального движения КА сводится к решению задачи Коши для системы дифференциальных уравнений движения и сопряженных множителей (1-2), (7) и оптимального управления (5-6). Для ее решения численного решения использовался метод Рунге-Кутты 4 порядка с постоянным шагом.

Введение расширенного вектора фазовых координат системы z = (r, A,, Vr, V,, m, Pr, P,,, Pv , P P_ )T r ϕm позволяет привести решение двухточечной краевой задачи к решению системы нелинейных уравнений:

f (z (t 0 ))= 0, (11) где f (z(t0)) - векторная функция невязок в конечный момент времени зависящая от начальных значений фазовых координат и сопряженных множителей в начальный момент времени z(t0). Для задачи достижения устойчивых точек либрации f (z(t0 ))=(r(T)-1, A,(T)-A,^, Vr (T), V, (T)- 1)T,

(12) а для пролета Луны на заданном расстоянии f ( ^z ( t 0 )) =⁽ r ( ^T ) — ¹ , ^A , ( ^T ) — , ^Pv_r ( ^T ) , P v , ( ^T )Y

Если определено начальное значение вектора z ( t ₀ ) , удовлетворяющее условиям (1 1 или 12) с заданной погрешностью при дифференциальных уравнениях (1-6), то требуемая задача оптимизации решена.

Функция невязок системы (11) очень чувствительна к начальным значениям подбираемых параметров _z и имеют многоэкстремальный, “овражистый” характер.

Для решения системы нелинейных уравнений (11) был использован модифицированный метод Ньютона с автоматической оцен- кой сходимости и изменением шага вычисления производных и ограничений на приращения. Для получения решений с различными значениями проектных параметров КА и граничными условиями перелетов использован метод продолжения по параметру, суть которого изложена ниже.

Пусть известно решение задачи оптимизации для некоторого фиксированного вектора проектно-баллистических параметров перелета b0 , т.е. известно значение расширенного вектора фазовых координат z(t0) доставляющего минимум критерию оптимальности T(b0). Требуется найти решение задачи в той же постановке, но для других параметров перелета b* . Если постановка задачи корректна, то при небольшом отличии b0 от b* решение задачи оптимизации (4) и критерий оптимальности (3) будут отличаться незначительно.

Разобьем отрезок от b ₀ до b_* на k частей и построим последовательность

Г" т-. b - bo bi = b о + —:— k

,

такую что при i = 0 ,

bi = b0 , а при i = k, bi = b*. Так как задача оптимизации при b0 решена, то известно начальное значение вектора z0 . Если считать, что при незначительном изменении вектора проектно-баллистических параметров значения вектора z изменяются линейно, то получим z (bi+1 )= z (bi)+ Ai(bi+1 - bi), где A =(z(bi.)-z(b-1 ^-bi-b-1 )1. (14)

Наиболее просто формула (13) выглядит в случае, когда в векторе b_i изменяется только одна переменная.

В работе [2] методика продолжения по параметру продемонстрировала высокую эффективность для решения задачи об опти- мальном по быстродействию движении КА в системе “Земля-Луна” в случае использования усредненных уравнений движения. В данной работе использование этого метода позволило получить решение поставленной задачи для различных значений проектнобаллистических параметров и граничных условий перелета.

Достижение точек либрации системы “Земля-Луна”

Рассматривается задача достижения точки либрации системы Земля-Луна L4 (КА движется по круговой орбите радиусом равным среднему радиусу орбиты Луны, опережая ее на 60є). Проектные параметры аппарата выбраны близкими к параметрам исследовательского КА Европейского космического агентства SMART-1: m₀ = 400 кг, P = 0,5 Н, с = 15 км/с.

Маневры набора скорости и увеличения большой полуоси орбиты аппаратами с двигателями малой тяги на низких околоземных орбитах хорошо изучены, в том числе с учетом возмущений от гравитации Луны и других небесных тел; нецентральности гравитационного поля и атмосферы Земли. С точки зрения влияния тяготения Луны на оптимальные законы управления и траектории движения интерес представляет поведение аппарата на высоких орбитах, поэтому в качестве стартовой рассматривается круговая орбита с большой полуосью a₀ = 100000 км.

Дифференциальные уравнения, описывающие поведение системы (1-7) позволяют осуществить непрерывное изменение параметра второго гравитирующего тела от нуля до требуемого значения. Это дает возможность использовать в качестве начальных приближений для подбираемых значений сопряженных множителей результаты решения задачи об оптимальном по быстродействию перелете между круговыми, компланарными орбитами при не фиксированной угловой дальности перелета в конечный момент времени. В этом случае, согласно условию трансверсальности РДф (Т) = 0. Если в уравнениях (1-7) положить и Л = 0 (гравита- цию Луны не учитывать), то в любой момент времени РДф (t) = 0 и порядок краевой задачи снижается до трех. Решение этой задачи и приближенные формулы для начальных значений сопряженных множителей были получены в работе [1].

Используя метод перемещения по гравитационному параметру второго притягивающего тела от 0 до µ_Л , определяется измененный вектор z ( t ₀ ) и соответствующее управление и траектория движения с учетом гравитации Луны с некоторой нефиксированной конечной угловой дальностью КА-Луна Д ф * ( Т ) = 60е. Затем условие трансверсальности в конечный момент времени Р _{Д ф} ( Т ) = 0 заменяется на условие достижения требуемой угловой дальности КА-Луна Д ф ( Т ) = Д ф_к . Теперь, осуществляя процедуру перемещения по переменной Д ф ( Т ) от Д ф * к Д ф_к =60е можно получить измененный вектор z ( t ₀ ) , оптимальные управление и траекторию при требуемых граничных условиях.

Использование такой методики позволяет не испытывать существенных трудностей в выборе начальных значений сопряженных множителей для решения краевой задачи и получить решения для различных граничных условий и проектных параметров КА.

На рис. 2а показана траектория, использующаяся в качестве начального приближения (достижение орбиты Луны с нефиксированной угловой дальностью Земля-Луна без учета гравитации Луны). На рис. 2б изображена итоговая оптимальная траектория достижения точки либрации L4, с учетом гравитации Луны и с фиксированной угловой дальностью в конечный момент времени Д ф ( Т ) = 60 ° .

На рис. 3-5 показаны зависимости компонент скорости КА и сопряженного множителя Р _{Д ф} на оптимальной траектории от угловой дальности перелета. Для сравнения приведены аналогичные зависимости для задачи пролета орбиты

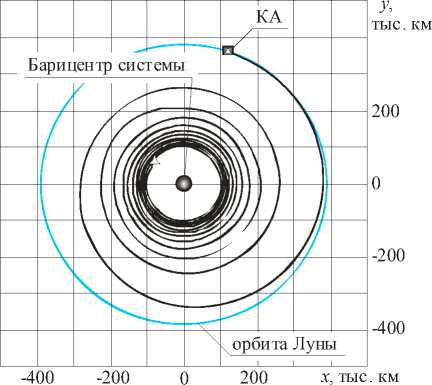
Рис. 2.

а – траектории достижения орбиты Луны без учета гравитации;

б – оптимальное по быстродействию достижение точки либрации L4 системы “Земля-Луна”

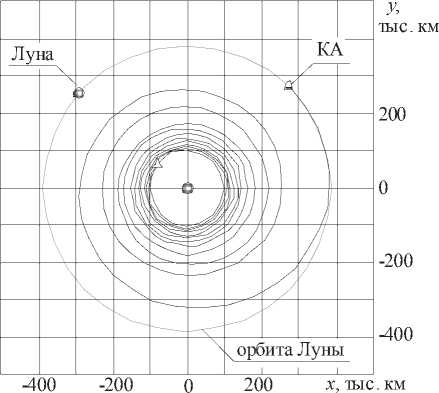
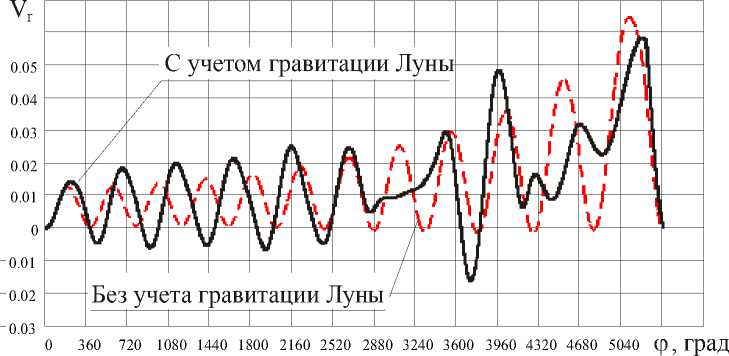
Рис. 3. Зависимость безразмерной радиальной составляющей скорости V_r от угловой дальности перелета для задачи достижения точки либрации L4

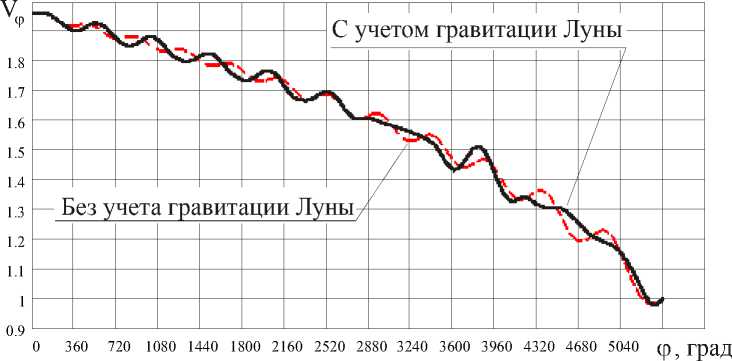
Рис. 4. Зависимость безразмерной составляющей скорости V _ϕ от угловой дальности перелета

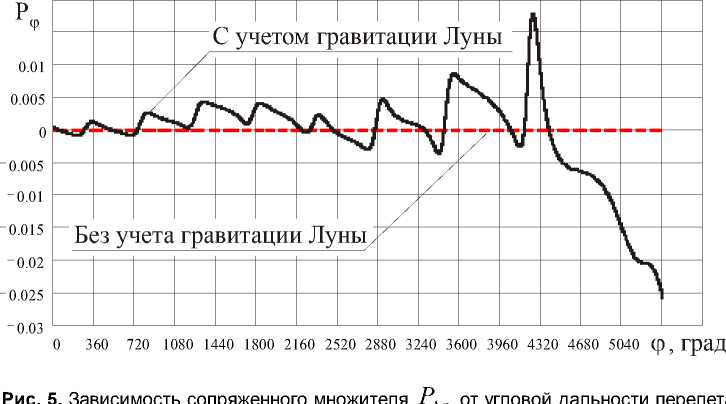
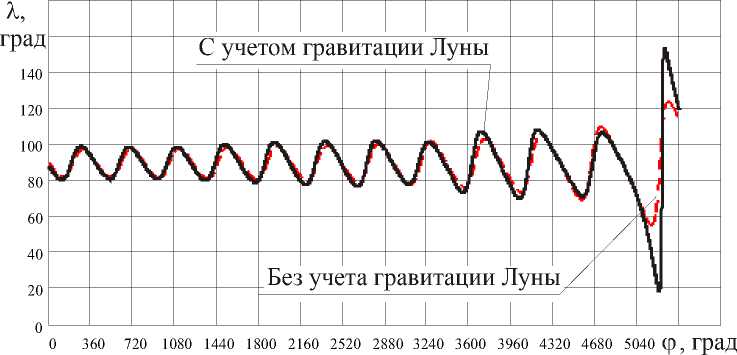
Рис. 6. Оптимальная программа управления, соответствующая достижению точки либрации L4 системы “Земля-Луна”

Луны без учета гравитации Луны использованные в качестве начального приближения (штриховые линии). На рис. 6 показана оптимальная программа управления, соответствующая достижению точки либрации L4.

Наибольшее влияние на оптимальное управление и изменение фазовых координат Луна оказывает на последних витках орбиты в моменты своего максимального сближения с КА. Особенно заметно это влияние на компоненты вектора скорости (рис. 3-4) и сопряженный множитель Р _{д ф} . Однако в целом длительность и угловая дальность перелета, оптимальное управление и траектории движения оказались близки к решению, использованному в качестве начального приближения.

Задача пролета Луны на заданном угловом расстоянии

Рассматривается задача пролета Луны при фиксированном угловом расстоянии КАЛуна в конечный момент времени. Начальные значения проектных параметров (кроме тяги двигателей) и стартовой орбиты выбраны такими же, как для задачи достижения точек либрации. Номинальная тяга двигательной установки увеличена до P = 1 Н.

В качестве начального приближения для решения задачи использовано решение задачи о достижении круговой орбиты с радиусом равным среднему радиусу орбиты Луны, описанное в работе [1]. Использование методики перемещения по параметру позволяет получить решения задачи оптимизации для различных граничных условий и проектных параметров КА.

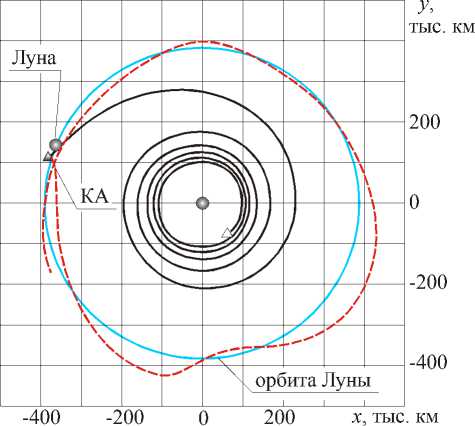
Рис. 7. Оптимальные по быстродействию траектории пролета Луны, ^Аф К ⁵ : а) монотонное изменение радиуса орбиты (T = 39,31 сут, А ф 0 = - 43 ° );

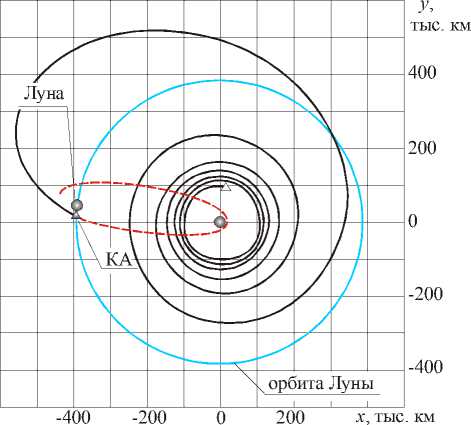
• б)    текущий радиус орбиты превышает радиус орбиты Луны (T = 68,13 сут, А ф ₀ = 87 ° )

  

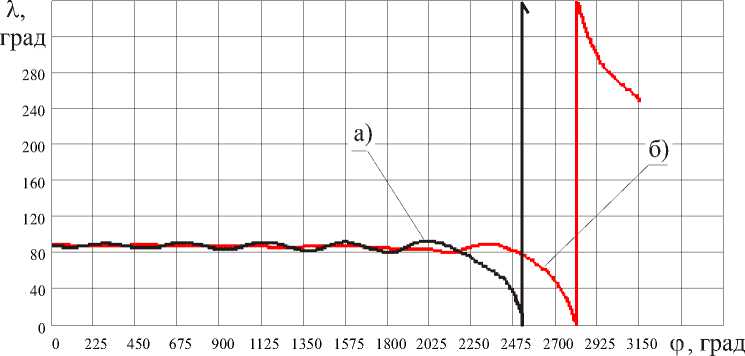
  Рис. 8. Оптимальная программа управления, соответствующая задаче пролета Луны А ф К = 5 ° а) монотонное изменение радиуса орбиты (T = 39.31 сут, А ф ₀ = - 43 ° );

  
  

• б)    текущий радиус орбиты превышает радиус орбиты Луны (T = 68.13 сут, А ф ₀ = 87 ° )

Показано, что гравитация Луны оказывает существенное влияние на оптимальный закон управления и соответствующую траекторию движения. Например, на рис. 7 изображены оптимальные траектории для пролета Луны на угловом расстоянии от нее 5є при старте с круговой орбиты с a ₀ =100000 км. Сплошной линией показано движение с включенным двигателем и оптимальным законом направления тяги. Пунктиром - траектории пассивного движения КА после завершения целевой задачи и отключения двигателей.

Задача оптимизации имеет многоэкстремальный характер. Во-первых, существуют различные классы решений, показанные на рис. 7а и 7б: траектории с монотонным изменением радиуса орбиты КА и траектории с увеличением радиуса траектории существенно больше радиуса орбиты Луны. Кроме того, в пределах одного класса возможны траектории, угловая дальность которых отличается на целое количество витков. Естественно, значение критерия оптимальности полученное для всех этих траекторий различно.

На траекториях с монотонным изменением радиуса орбиты (рис. 7а), КА после выключения двигателей оказывается захваченным гравитационным полем Луны и выходит на замкнутую селеноцентрическую траекторию. Эти траектории могут использоваться для формирования орбиты вокруг Луны с заданными параметрами. Траектории с немонотонным изменением радиуса орбиты (рис. 7б) характеризуются большой относительной скоростью КА – Луна в момент отключения двигателей и могут быть использованы для формирования траектории возвращения к Земле.

На рис. 8. показана программа оптимального управления для монотонных и немонотонных оптимальных траекторий.

Таким образом, предложенная методика показала свою эффективность для оптимизации сложных многовитковых траекторий движения КА с двигателями малой тяги в поле притяжения двух тел. Полученные оптимальные законы управления и соответствующие ему траектории движения могут быть использованы для решения задач формирования заданных селеноцентрических орбит.