Оптимизация «естественного» переходного процесса

i 0( t ) = E ■ e ^- t ^{/ т} , (1)

R где т = C• R - постоянная времени цепи.

В любой конкретный момент t 1 процесса величина p ( t 1 )= R·i 0 (t 1 )² мощности соответствует точке минимума функционала F цепи [1]:

F = R ■ i 0( t 1 ) 2 - 2 • [ E - uC ( t 1 ) ] - i 0( t 1 ), (2) где uC(t ₁ ) – напряжение на емкости.

Отметим, что (2) не только равен мощности на R в любой момент, но и следующее из него уравнение dF/di0=0 тождественно уравнению Кирхгофа. Очевидно, именно следование этому уравнению при любом t и обеспечивает переход локальной оптимальности процесса по потерям в глобальную оптимальность по потерям. Но это – при условии неизменности цепи. Поставим вопрос о возможности организации такого процесса, который на концах заданного временного интервала k·τ давал бы состояния по (1), обусловленные общим назначением устройства, но имел меньшую величину энергии потерь WR на этом интервале. Осуществимость такой оптимизации с помощью, например, некоторого дополнения к RC-цепи, могла бы продемонстрировать существование ненулевой добавки f(t) к току (1). Добавка не должна менять состояний цепи по (1) на концах интервала k·τ, то есть, иметь свойства f(0)=0 и f(k·τ)=0. Например, этим требованиям удовлетворяет синусоида тока амплитудой Im и частотой ω=2π/ kτ. Тогда общий ток:

i ( t ) = i 0 ( t ) + I m -sm(2 n t / к т ) . (3)

Итоговая величина энергии, выделившейся на резисторе R , в этом случае определится интегралом:

к ■ т

W_R = j R •[ i 0 ( t ) + I m ■ sin ( 2 n t / к т ) ]² ■ dt . (4) 0

Представляется логичным считать, что если уравнение dWR/dlm = 0 дает решение Im=0, то траектория (1) процесса соответствует не только локальным минимумам мощности потерь в любой точке интервала, но и доставляет минимум общей энергии потерь на заданном интервале. Очевидно, в таком случае процесс по (1) является самым выгодным между концами интервала k·τ. Проверка показывает, что это не так, поскольку уравнение для экстремума dWR /dim = 0, получаемое после дифференцирования несложного интеграла (4), дает для Im ненулевое в общем случае решение:

Im

E ^{4 п}( e ^к - 1 )

R ’ к ² + 4 п ²

В частном случае при к = 0 выражение (5) действительно дает нулевое решение Im=0. Но при к ^ 0 решение не является нулевым. Таким образом, процесс (1) локально (при к = 0 на отрезке dt) оптимален. Но складывающаяся при этом общая траектория может быть улучшена с целью сниже- ния энергии потерь для всего конечного интервала k·τ. На рис. 1 представлены результаты расчетов функции энергии WR (Im) потерь и графики токов i (t), i0 (t) для цепи с параметрами R =15, C=10"4 и E=100. Формула (5) дает оптимальную амплитуду токовой добавки к (1) величиной Im=–1,642. Эту величину подтверждает и график WR (Im).

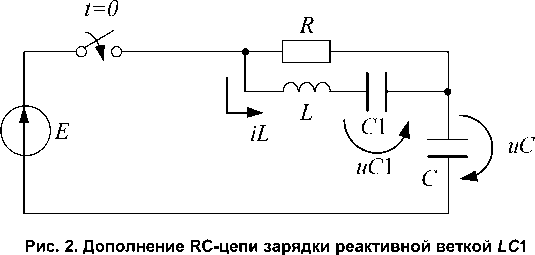
Отметим центральный посыл статьи, заключающийся в первоначальном конструкторском игнорировании тождества «выгодно локально – выгодно глобально». Разница между локальным ( к = 0 ) и глобальным ( к ^ 0 ) здесь объясняется просто – функционал (2) отличается от функционала для любой возможной схемы, физически реализующей добавку f ( t ) . На рис. 2 представлен пример одной из таких схем, относительно близко воспроизводящей ток по (3) и мотивирующей к использованию такой тактики.

Схема с относительно хорошо известной «ускоряющей LC 1-цепью» (рис. 2) частично реализует добавку f ( t ) и действительно, как показывает расчет, обладает свойством снижать итоговую оценку W_R , попутно улучшая и некоторые другие показатели цепи на интервале k·τ .

Для проверки полученных оценок воспользуемся стандартной процедурой составления дифференциальных уравнений состояния цепи, [3], и построим на их основе численную модель интегрирования в рамках алгоритма явного метода Эйлера для переменных uC 1, iL и uC состояния цепи по рис. 2:

f uC1 k ) iL k

V uCk J rr

–1 L

V

f uC1 к -1 )

iL k –1

V uC k -1 J

1 С 1

1 С

–1 L –1

fuC1 k-1' iLk-1

V uC k -1 J

• A t

A

+

E L E

• A t .

R • C J

E–uС iRk :=-------L;

k R

i k : = ^iL k ^{+ iR} k •

V R • C J

Приняв за длительность отрезка описания процесса величину 5· R·C , расчет по (6) проведем для цепи с параметрами E =100, R =15, C =10^–4 при величине L , определяемой для задаваемой С 1 че-

рез оценочную величину частоты резонанса с периодом 3* R*C реактивной ветви © =( L • C 1)”^0,5= =2·π/3· R·C . Расчет энергий WR и W 0 потерь на R проведем по формулам:

wR k : = R ( iR_k ) 2 •A t ;

N w^R : = ^ w^Rk; k = 0

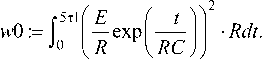
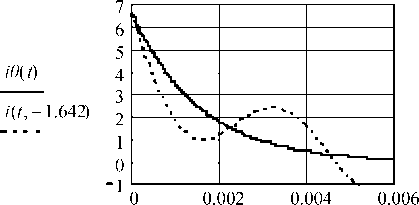
На рис. 3 представлены результаты описываемого численного моделирования в виде графиков uC ( t ) , i ( t ). Для сравнения, там же графики uC 0( t ) и i 0( t ) для случая цепи без ветви LC 1.

Для этой же цепи на рис. 4 представлены зависимости доли W_R/W 0 (в процентах) потерь от величины С 1 при наличии ветви LC 1 от потерь в

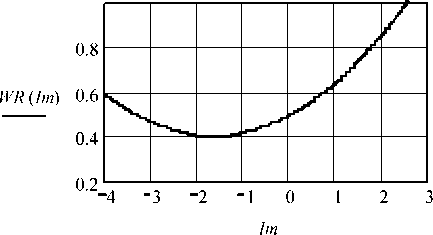
Рис. 1. Оптимум I m , процесс i ( t , I m ) с добавкой и исходный процесс i 0 ( t )

Грамм М.И.

Оптимизация «естественного» переходного процесса

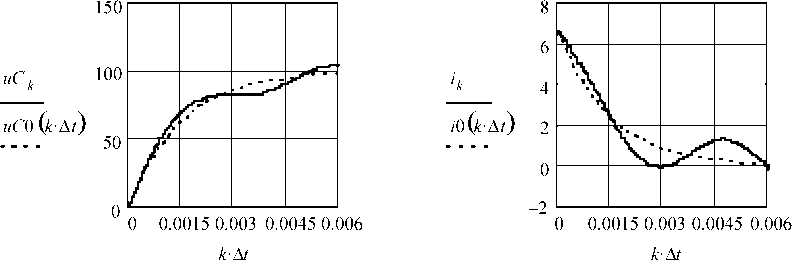
Рис. 3. Сравнение графиков напряжения и тока исходной цепи и цепи RCLC 1

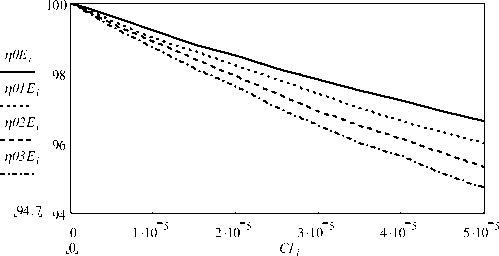
Рис. 4. Снижение потерь при увеличении емкости С 1 для разных uC 1(0)

исходной RC -цепи для разных величин uC 1(0) начального напряжения на C 1 (оно указано в долях от Е : 0; 0,1; 0,2; 0,3). Видим, что действительно введение «ускоряющей ветви» с элементами L и C 1 снижает показатель энергии резистивных потерь на заданном интервале. Доля снижения зависит и от величины uC 1(0).

Заключение. Таким образом, минимаксный подход к оптимизации процессов в цепях может быть реализован как прямое применение принципа минимума потерь к улучшаемой исходной цепи в виде оценок абстрактных возможностей улучшения ее энергетических характеристик на конкретном отрезке времени. Такое предварительное исследование шансов на улучшение энергетических показателей делает мотивированным дальнейший поиск конкретных схемных решений для снижения резистивных потерь.

Рассмотренный выше простой пример оптимизации переходного процесса в RC-цепи имеет и самостоятельное значение как вариант совершенствования схем компенсированных преобразователей [4]. Именно внутри цикла такого преобразователя «ускоряющая» емкость С1 оказывается заря- женной uC1(0)≠0, а начало работы основной емкости С можно спланировать на наиболее выгодный момент весьма сложного процесса (например, момент t=0,03 по рис. 3). В этом случае, как показывают оценки, экономия потерь на R описанным выше схемным решением может составить 20 % и более.