Оптимизация функции управляющего воздействия для электропривода с синхронной реактивной машиной с независимым управлением по каналу возбуждения

Пространственное распределение магнитодвижущей силы (МДС) двигателя в электроприводах (ЭП) переменного тока, в случае неучета высших гармоник, при определенной фазной обмотке совпадает по форме с управляющим сигналом во времени. Это позволяет иначе сформулировать задачу и оптимизировать форму пространственной МДС статора, т. е. линейную плотность поверхно- стного тока.

В качестве критериев оптимизации необходимо выбрать параметры, которые обеспечат высокие массогабаритные показатели ЭП, например, электромагнитного момента двигателя к значению потерь в обмотке статора. Известно, что электромагнитный момент определяет габарит электриче- ского двигателя.

Не обращаясь к частному, МДС, которую создает обмотка статора, можно определить:

Здесь C - постоянная, определяемая в случае симметричной формы МДС в зазоре как у (т) = у(—т); т - полюсное деление; x(t) - линейная плотность тока поверхностного тока [1, 13].

Касательное усилие, которое действует на ротор в точке t,

z(t) = x^) •y(t).                            (2)

Для того чтобы учесть явнополюсную конструкцию ротора (например, синхронный реактивный двигатель с независимым управлением по каналу возбуждения), определим функцию [2]:

(tx = (z(t), где z(t) > 0

Величина окружной силы, которая создает электромагнитный момент двигателя, пропорциональна площади под кривыми a — b — с, d — е — f (рис. 1):

S = £ u(t)dt. (4)

Статор

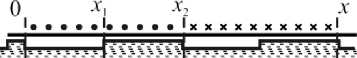
Ротор

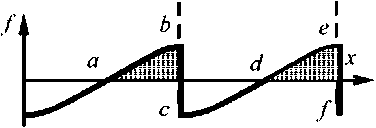
Рис. 1. График удельной касательной силы в электрической машине

При этом из практики проектирования одного из узлов электропривода – электромеханического преобразователя – известно [3], что габарит элек- тродвигателя определяется электромагнитным моментом, который, в свою очередь, обусловлен раз- виваемой двигателем окружной силой. Исходя из этого, в качестве критерия оптимизации целесооб- разно выбрать показатель [4]: 5

• ^q    "T+т TTL .

x ^z dt

J —т

Величина q может быть рассчитана через от-

ношение значения электромагнитного момента двигателя к значению потерь в обмотке статора при единичных осевой длине ротора, окружности расточки статора, активном сопротивлении обмотки статора. Числитель и знаменатель величины q в одинаковой степени (во второй) зависят от тока статора, т. е. данная величина – величина нулевой размерности относительно значения тока.

В качестве целевой функции будет выступать линейная плотность поверхностного тока х = x(t), где t - координата, которая отсчитывается вдоль расточки статора.

Техническое задание на проектирование, стандарты и другие директивные документы, геометрические, физические и технико-экономические особенности проектирования привода накладывают определенные ограничения на изменение параметров объекта оптимизации.

Максимальное значение индукции в зазоре и допустимая по нагреву величина тока являются наиболее значимыми ограничениями в электрическом двигателе [5].

Для рассматриваемого случая примем следующие ограничения:

• – насыщение магнитной системы:

• У < У тах ;                                 (6)

  – ограничение по нагреву:

2т S -Т x ² (t)dt < Х тах .                       (7)

Уравнения связи, которые характеризуют свойства объекта оптимизации, могут быть представлены нагрузочными и скоростными диаграммами, учитывающими приложенные возмущения [6]:

S-T x(t)dt = 0;

z(t), где z(t) > 0

u(t) = |

Вопросы оптимизации линейной плотности поверхностного тока были рассмотрены для различных случаев питания обмоток статора: индивидуальные источники питания на каждой фазе; два автономных инвертора, которые работают параллельно; схема при проводимости вентилей 120 ° . При этом предельное значение МДС было ограничено для того, чтобы учесть насыщение магнитной системы машины.

В качестве исходного графика линейной нагрузки была принята прямоугольная форма токов с возможностью регулирования каждого пазового тока независимо от других, при этом магнитная цепь электродвигателя считалась линейной. При относительной величине полюсной дуги b = 0,5 оптимум был найден в случае равных величин токов в пазах.

Для того чтобы учесть насыщение, кривая намагничивания 1 была аппроксимирована ломаной 3 (рис. 2), при этом коэффициент к = В₂/В₁ (где В_г -индукция в зазоре в идеальной магнитной системе, В₂ - максимальная реальная индукция в зазоре) учитывал степень насыщения электрической машины.

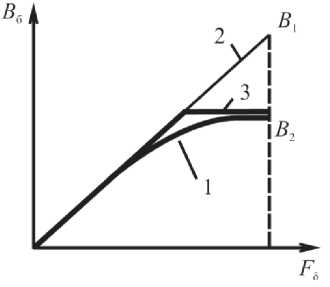
Рис. 2. Реальная (1), идеальная (2) и расчетная (3) кривые намагничивания электрической машины

В данном случае оптимальное значение полюсной дуги увеличилось, а в качестве оптимальной формы линейной нагрузки осталась горизонтальная прямая (рис. 3). При к = 0,5 величина q снизилась на 42 %, полюсная дуга изменилась до b = 0,63.

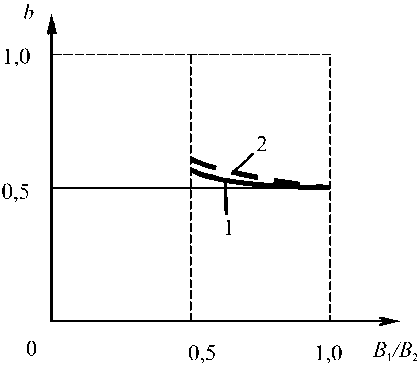
Рис. 3. Зависимость полюсной дуги b от степени насыщения магнитной системы: 1 – при независимом питании обмоток; 2 – при питании обмоток от двух трехфазных инверторов напряжения

При питании электропривода по схеме, когда обмотки фаз статора собраны в две звезды, которые сдвинуты на 30 электрических градусов в пространстве, и подключены к двум автономным инверторам, работающим параллельно, наибольшая величина q была зафиксирована при проводимости вентилей 180 градусов, но это значение на 11 % меньше, чем в исходной схеме. Показатель b равен 0,5. Полуволна тока одной фазы статора СРМНВ, которая может быть принята оптимальной, состоит из нескольких горизонтальных отрезков, продолжительность которых равна 60 градусам (рис. 4). Средний отрезок по амплитуде в два раза больше, чем крайние. Данный показатель снижается, если учитывать насыщение магнитной системы электрического двигателя. Так при к = 0,5 показатель q уменьшается на 50 %, а b

Электроэнергетика

принимает значение 0,67. Если переходить на проводимость вентилей 120 градусов, то неэффективность использования двигателя увеличится на 19 % [7–9, 12].

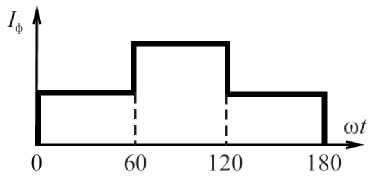
Рис. 4. Форма полуволны тока фазы статора СРМНВ при питании от трёхфазного инвертора напряжения

Проведено сравнение СРМНВ с традиционной реактивной машиной (питание осуществляется синусоидальным напряжением) [10]. Линейную плотность поверхностного тока можно описать уравнением

А(х) = А_т sin ( П х),                       (9)

а МДС

Г(х) = J A(x)dx + С =

=-А_т cos ( П х) • П .                      (10)

Выражение /. = А(х) • В ₆ (х) позволило определить удельное касательное усилие. Для длины полюсной дуги а₆ = 0,5 определили электромагнитный момент:

М = ^6 J^2 А(х) • Вб(х) • dx =

= ^6 Г^ т ^sin ( П ^х) • П ^А т cos ( П ^х) • т ; • ^dx =

■■   П (-£cos(2 П 2 = _к^ ,   ⁵       (11)

где к = ⁷1 б^{Т ;} .

²    ^ 6

Критерий оптимизации определялся выраже- нием q =

= к -^т5 . 2л ²

м ^ Г ⁵

Для электропривода с СРМНВ этот показа- тель равен [11]

q = кт ² - .

4        4

Итак, в случае питания синхронной реактив- ной машины синусоидальным напряжением величина q снижена на 23 % по сравнению с исходным случаем. А если учесть, что синхронные реактивные двигатели традиционно работают в схемах

Величина критерия оптимизации в зависимости от способа питания силовых цепей

Варианты питания силовых цепей q, % Индивидуальные источники питания 42 Проводимость вентилей 180 градусов 89 Проводимость вентилей 120 градусов 81 Проводимость вентилей 60 градусов 50 Синусоидальное напряжение 77 Частотное регулирование 27 с частотным регулированием (отсутствуют датчики положения ротора) или напрямую от сети переменного тока, где приходится учитывать запас статической устойчивости двигателя, то q уменьшается еще на 50 % [12]. Рассмотренные данные были сведены в общую таблицу [14].

Рассмотренные аналитические методы вполне способны дать первичную оценку решениям при выборе источника питания силовых цепей электромеханического преобразователя, что существенно сокращает временные затраты на этапе выбора электрооборудования. При этом не отвергается возможность сочетания упрощенных методов и вариантов расчета по детализированным схемам.