Оптимизация геометрических условий проведения абсорбционного мёссбауэровского эксперимента

Одним из важнейших факторов, влияющих на параметры мёссбауэровского спектра, является степень коллимированности пучка гамма-квантов, которая определяется геометрическими условиями проведения эксперимента.

Несмотря на то что в имеющихся работах [1–3] приведено математическое решение задачи о влиянии геометрических факторов на форму мёссбауэровского спектра, а в [4] описан алгоритм программы, моделирующей спектр с учетом заданных геометрических условий, в них отсутствуют критерии, на основе которых можно давать рекомендации по выбору оптимальных геометрических условий.

Настоящая работа направлена на разработку методики выбора оптимальных геометрических условий проведения абсорбционного мёссбауэровского эксперимента с целью уменьшения искажения формы и положения экспериментальных спектральных линий, что непосредственно должно влиять на возможности мёссбауэровской спектроскопии при проведении как качественного, так и количественного анализов.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

В рассматриваемом нами случае эксперимента на пропускание (рис. 1) основными геометрическими параметрами, влияющими на форму спектральных линий, являются размеры детектора ( R d ) и источника ( R s ), а также расстояние между ними ( l ). Очевидно, что при увеличении радиусов R d и R s и уменьшении расстояния l будет расти как светосила эксперимента, так и степень неколлимиро-ванности пучка мёссбауэровских квантов (угол θ = 2arctg ^{R d} ).

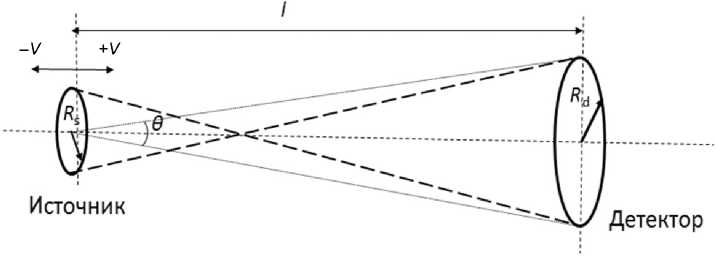
Рис. 1. Взаимное расположение источника и детектора

В качестве примера работ, посвященных изучению влияния геометрических условий проведения мёссбауэровского эксперимента на параметры спектра, следует привести [1–5]. Результаты этих исследований показывают, что увеличение расходимости пучка гамма-квантов приводит к искажению спектральных линий (косинусный эффект). Во-первых, наблюдается смещение положений спектральных линий в сторону бόльших скоростей, причем смещение Δv пропорционально модулю резонансной скорости (доплеровской добавки) v0 для данной линии и хорошо приближается л т 1 - cos 6

[1, 3] зависимостью A v ( v 0 ) =-------- v ₀ , где

1 + cos 6 0

R + R _

6 0 = arctg^-^—-. Во-вторых, спектральные линии существенно уширяются и приобретают асимметрию с более пологим краем, обращенным в сторону бόльших скоростей. Данный эффект также пропорционален v 0 .

Так как экспериментатор заинтересован одновременно и в максимальной светосиле эксперимента, и в минимальном искажении формы и положений спектральных линий, закономерен вопрос о выборе оптимальных геометрических условий. Из вышесказанного следует, что такие условия будут зависеть от положения линий в мёссбауэровском спектре ( v 0 ) : чем больше максимальная скорость наблюдения резонанса, тем сильнее будет проявление косинусного эффекта и тем строже требования к коллимированности пучка.

Форма линий испускания источника и поглощения резонансными атомами, описывается распределением Лоренца:

L ( v ) =

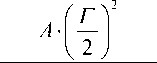
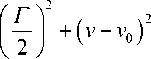
где v ₀ — химический сдвиг относительно некоторого репера, мм/с; Γ — ширина линии на полувысоте, мм/с; A — амплитуда линии.

Рассмотрим случай движущегося источника и неподвижного поглотителя. В условиях идеальной коллимации интеграл пропускания, определяющий количество зарегистрированных квантов для данной скорости I ( v ), будет иметь следующий вид [6]:

I ( v , d ) = I _s te - "d tot x

(1 - f s ) + f

x

to j Ls( vv) e - La(v') d 1 d )dv'

-to

Здесь I S — интенсивность квантов, испущенных мёссбауэровским источником (имп/с); µ — массовый коэффициент нерезонансного поглощения излучения (см²/г); d tot — общая толщина поглотителя, включающая содержание резонансного изотопа и матричных элементов; d — толщина поглотителя по резонансному изотопу (г/см²); f s , f a — факторы Лэмба—Мёссбауэра источника и поглотителя; v — скорость источника (мм/с); t — время накопления спектра (с); L s , L a — профили линий испускания и поглощения для источника и поглотителя соответственно; d eff — безразмерная эффективная толщина поглотителя по резонансному изотопу.

Эффективная толщина определяется как d ff(d) = wf g„d —A, где w — степень обогащения eff a 0 M поглотителя резонансным изотопом; σ0 — максимальное сечение резонансного поглощения (см2); NA — постоянная Авогадро (моль–1) и M — молярная масса поглотителя (г/моль).

Интеграл пропускания (1) с учетом геометрических параметров проведения эксперимента определяется выражением:

I ^real( v , d , r_s, r d ) =

θmax f I(v • cos 6,

₀           cos θ

) f ( θ , r s , r d )d θ

,

θ max

J f ( 6 , r s , r d )d 6

RR где rs = -p > rd = -p > 6max = arctg(rs + rd), а f(θ, rs, rd) — функция углового распределения плотности излучения, описанная в работе [1].

РЕЗУЛЬТАТЫ

На основе выражения (2) были проведены модельные расчеты мёссбауэровских спектров α-Fe с разной степенью коллимации пучка гамма-квантов. Спектр α-Fe представляет собой магнитный секстет с нулевыми изомерным сдвигом и квадрупольным расщеплением. Данный секстет удобен для изучения влияния положения линии в спектре на поведение основных спектральных параметров при ухудшении коллимации. Его можно рассматривать как совокупность независимых линий с различным модулем скорости резонанса: v 01 = 5.312 мм/с — для внешних линий, v 02 = = 3.076 мм/с — для центральных и v 03 = = 0.840 мм/с — для внутренних.

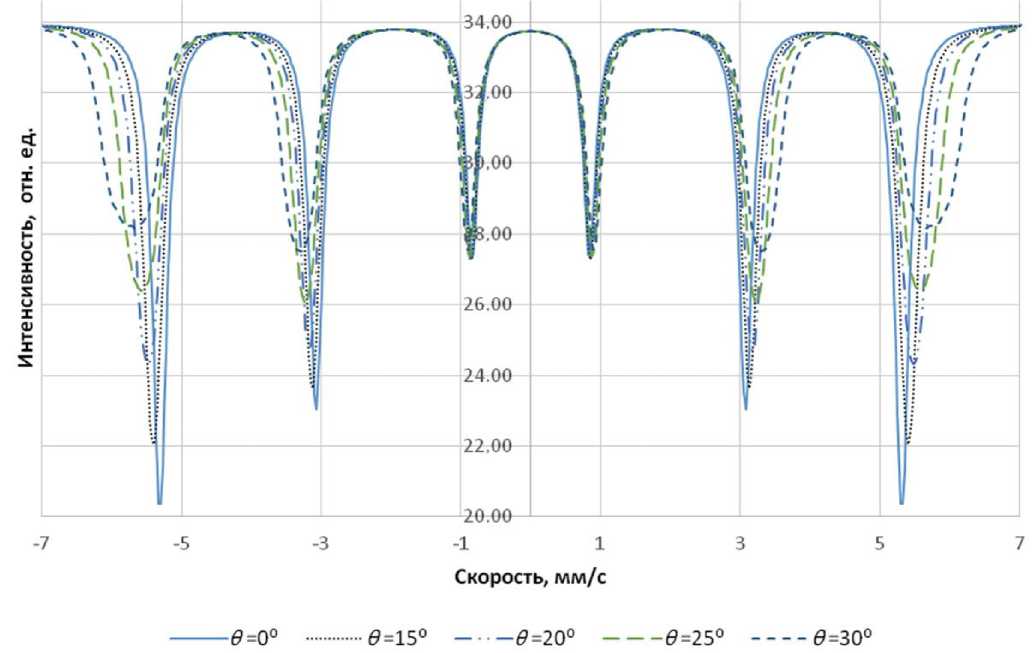
Рис. 2. Модельные мёссбауэровские спектры α-Fe c с различной степенью коллимации пучка γ-квантов

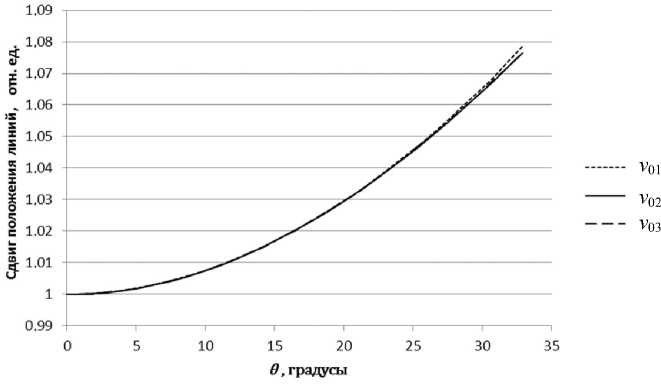
Рис. 3. Зависимость величины нормированного сдвига положения спектральных линий от угла расходимости θ для внешних ( v 01 ), центральных ( v 02 ) и внутренних ( v 03 ) линий мёссбауэровского спектра α-Fe

На рис. 2 представлен набор модельных спектров, отвечающих точечному источнику (Rs = 0) и различным углам расходимости θ (см. рис. 1) в диапазоне от 0 до 30º. Толщина железа составляет 0.017 г/см2 и соответствует оптимуму отноше- ния сигнал/шум в соответствии с [7].

Из рисунка видно, что с ухудшением коллимации излучения спектральные линии уширяются и сдвигаются в сторону бόльших скоростей. При этом искажение линии тем сильнее, чем больше модуль ее скорости, отвечающей резонансу. На рис. 3–5 показаны зависимости основных спектральных параметров от угла θ. Все параметры нормированы на их значения, соответствующие случаю идеальной коллимации (θ = 0º).

На рис. 3 показана зависимость нормированно-

- A v го сдвига положения спектральных линий i v0i

(i = 1, 2, 3) от угла расходимости θ. Из рисунка видно, что ход зависимости одинаков для всех линий. Нормированный сдвиг, таким образом, не зависит от положения линии в мёссбауэровском спектре и определяется только углом θ.

На рис. 4 и 5 показаны зависимости нормиро-A ванных амплитуд линий i и ширин линий

Γ на половине высоты ⁱ от угла расходимости θ .

Γ 0 i

Видно, что ход зависимостей сильно различается для внешних, центральных и внутренних линий спектра α-Fe . Наибольшему искажению (уширению и уменьшению амплитуды) подвержены внешние и в меньшей степени центральные линии. Амплитуда внутренних линий спектра, находящихся вблизи нуля скорости, практически не изменяется, а их ширина возрастает не более чем на 25 % при 6 <  30 ° .

Из рис. 3–5 хорошо видно, что изменения основных спектральных параметров линий α-Fe пренебрежимо малы в диапазоне θ 0–10º. Однако в общем случае линий с произвольной скоростью резонанса v 0 нельзя однозначно указать допустимый интервал θ и следует рассмотреть зависимость θ crit ( v 0 ), где θ crit — максимально допустимый угол расходимости, не приводящий к сильному искажению спектральных линий. Для этого в качестве требований к геометрическим условиям проведения эксперимента рассматривались следующие:

• 1)    отклонение положения линии должно составлять не более 10 % от собственной ширины (условие 1);

• 2)    уширение линии не должно превышать 10 % (условие 2).

Выполнение данных требований в большинстве встречающихся на практике случаев не приведет к искажениям спектральных линий, затрудняющим интерпретацию спектра.

На рис. 6 показан ход зависимости максимально допустимого угла расходимости θ (критический угол) от положения линии в спектре для обоих требований. Из рисунка видно, что первое требование накладывает более строгие условия на геометрические условия проведения мёссбауэровского эксперимента, поэтому второе требование можно не рассматривать.

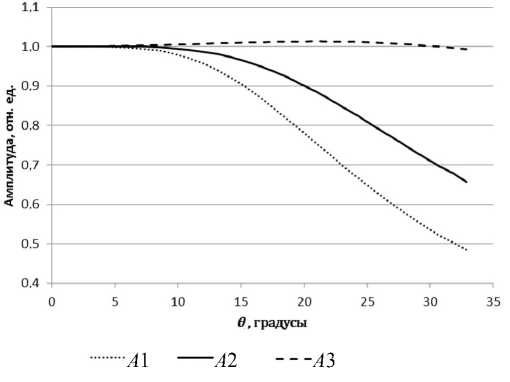
Рис. 4. Зависимость величины нормированной амплитуды от угла расходимости θ для внешних ( A 1), центральных ( A 2) и внутренних ( A 3) линий мёссбауэровского спектра α-Fe

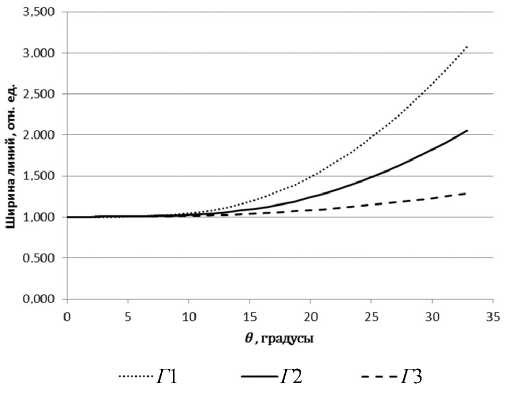
Рис. 5. Зависимость величины нормированной ширины линии на половине высоты от угла расходимости θ для внешних ( Г 1), центральных ( Г 2) и внутренних ( Г 3) линий мёссбауэровского спектра α-Fe

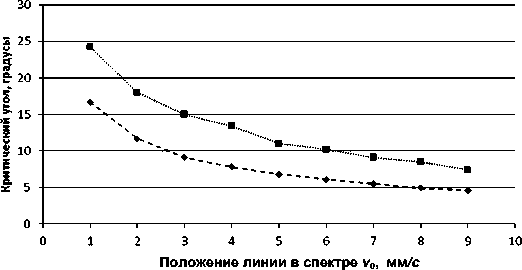
-♦- - Условие 1 .....■.....Условие 2

Рис. 6. Зависимость максимально допустимого угла расходимости от положения линии в мёссбауэровском спектре

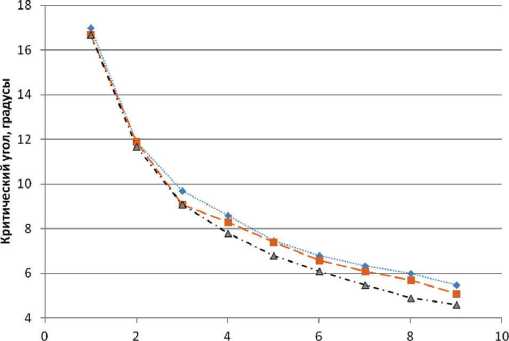
Положение линии в спектре v0, мм/c rs = 0 rs = 0.3 rs = 0.6

Рис. 7. Зависимость максимально допустимого угла расходимости от положения линии в мёссбауэровском спектре для источников различных размеров

Реальный источник всегда имеет конечные, отличные от нуля, размеры, что также ухудшает коллимированность излучения. На рис. 7 показаны аналогичные зависимости θ crit ( v 0 ) для случая неточечного источника ( r s = 0.3 и r s = 0.6). Видно, что при переходе к неточечному источнику вид требования к степени коллимированности пучка не сильно возрастают. Данные зависимости хорошо аппроксимируются степенными функциями, и при r s ≤ 0.6 для оценки критического угла расходимости в зависимости от положения линии в спектре ( v 0 ) можно пользоваться выражением ^ crit ( v 0 ) = 17 v 0 - 0.6 . Расчеты показали, что данная формула остается справедлива для различных поглотителей в области приближения тонкого поглотителя ( d eff ≤ 1) .

ВЫВОДЫ

На основе математической модели, разработанной в [1], были смоделированы серии мёссбауэровских спектров α-Fe с различной степенью коллимации пучка гамма-квантов. Проведен анализ искажения формы спектральных линий в зависимости от величины доплеровской добавки (отклонение от нулевой скорости), который позволил сформулировать основные требования к геометрическим условиям проведения эксперимента и показать зависимость допустимого угла расходимости от положения линии в мёссбауэровском спектре. Данная зависимость позволяет экспериментатору на практике выбирать необходимые геометриче- ские условия, чтобы добиваться минимальных искажений спектральных линий. Такая процедура является необходимой для использования в мёссбауэровской спектроскопии как в качественном, так и в количественном анализe.