Оптимизация геометрии высокоскоростного роликового подшипника при перекосах колец

Работоспособность роликовых подшипников существенно снижается при перекосах колец подшипников в опорах авиационных газотурбинных двигателей, где перекосы возникают вследствие деформаций тонкостенных валов и корпусов в рабочих условиях.

Повышение работоспособности подшипников и снижение неравномерности распределения нагрузки по линии контакта при перекосе обеспечивается, как правило, профилированием образующей ролика [1-5]. Нами рассмотрено распределение нагрузки по линии контакта при перекосе роликов с различной формой бомбины. Показано, что у высокоскоростных подшипников при перекосах условия контактирования ролика с наружным и внутренним кольцами различны. Это необходимо учитывать при выборе образующей ролика и внутренней геометрии подшипника в целом. При этом беговую дорожку наружного кольца целесообразно выполнять цилиндрической, а профилировать только образующую роликов и беговую дорожку внутреннего кольца.

Рассмотрим характеристики трех типов роликов: цилиндрического, с радиусной бомбиной и с логарифмическим профилем бомбины. При этом с целью унификации исходных данных для всех профилированных роликов задаются лишь величина Д ф , величина фаски у торца 1 т а также длина цилиндрического пояска l_c (рис. 1).

Для ролика с радиусной бомбиной радиус профиля образующей является константой и определяется по формуле:

Rф =

iAt -iA фp ф

2 Д ф

Для ролика с образующей, описываемой логарифмической кривой, профиль ролика определяется выбранным участком логарифмической кривой.

Для логарифмического профиля принимаем функцию

При этом начало оси координат приводим к торцу ролика. Точка, соответствующая концу бомбины, будет иметь координату X = I t + 1 ф •

Тогда величина параметра логарифмического профиля определится по формуле:

а* = —Дфф   ln (1ф /1Т +1) •

Радиус профиля является переменной величиной и в произвольной точке с координатой x определяется по выражению [6]:

Кф = (1 + (dy/dx)2 ^ d2 2у/dx21.

После дифференцирования, подстановки и преобразований получим формулу для расчета радиуса кривизны профиля:

К ф =

⁽ а ф

+ X ²

)1 , 5

а ф x

Так как х >  1 т и, следовательно, а ф <<  х в практических расчетах можно принять:

R ф * х /а ф •

Профиль образующей беговой дорожки внутреннего кольца принимаем соответствующим типу профилированного ролика, т.е. цилин-

/

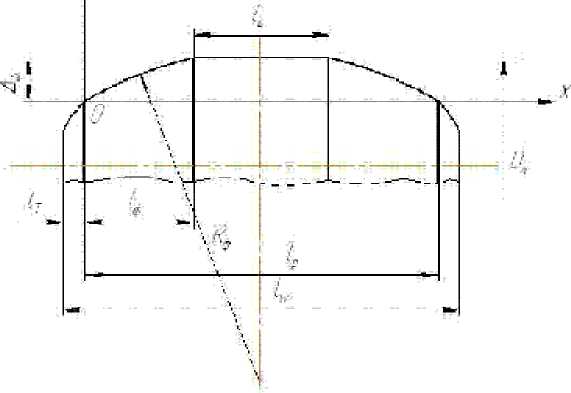
Рис. 1. Схема профиля бомбинированного ролика

дрическим, с радиусной бомбиной или с бомби-ной логарифмического профиля.

При этом с целью унификации исходных данных для всех профилированных колец зада-

ются лишь величина бомбины А к и длина ци линдрического пояска l_c , а также величина фаски l_Тк у торцов кольца (рис. 2). При этом длину

-

цилиндрического пояска принимаем одинаковой для кольца и ролика.

Для кольца с радиусной бомбиной радиус профиля является константой и определяется по формуле:

При этом длину l_к рабочего участка беговой дорожки кольца определим с учетом фасок у тор-

цов: l_к = B — 2 1_Тк . Длину бомбины кольца оп ределим по формуле: l ф_к = ( 1 к — l c )/ 2 .

Для кольца с образующей, описываемой ло гарифмической кривой принимаем функцию

У = a к In (x/ (/^ + ф )).

При этом начало оси координат приводим к торцу кольца. Точка, соответствующая концу бомбины, будет иметь координату x = ¹Тк + ¹фк .

Тогда параметр логарифмической кривой определится по формуле:

А

a , = —z----к-----v

.

фк Тк

Распределение нагрузки по линии контакта при перекосе роликов является неравномерным. Для его расчета разработаны достаточно точные методы [5,7], основанные на положениях теории

-

-

упругости. Однако в связи с большой трудоем костью вычислений для решения задач опреде ления оптимального профиля образующей роли ков и колец используем упрощенное решение.

-

-

-

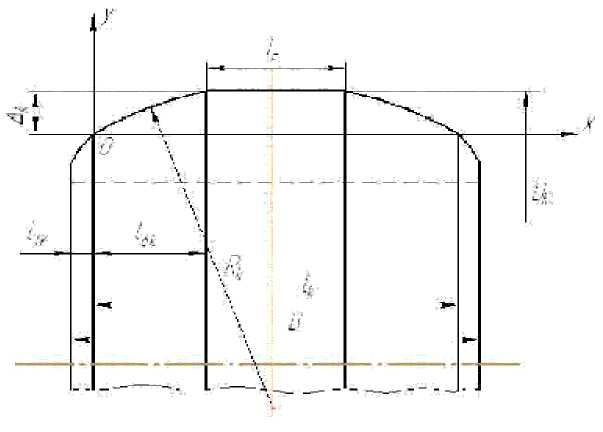
Рис. 2. Схема профиля кольца с бомбиной

При этом область контакта ролика разбивается на n участков длиной A l = l_p fn - Приведенный радиус кривизны в каждом сечении в контакте ролика с кольцом определяется по формуле:

R ■ прi

R 1 i R 2 i

R 2i ± R п-

.

Здесь: R _{1 i} – радиус ролика в данном сечении; R _{2 i} – радиус кольца. При этом знак плюс принимается для контакта ролика с внутренним кольцом, а минус – для контакта с наружным.

Здесь для внутреннего кольца принимаем знак минус, для наружного – плюс.

При определении радиуса ролика координаты сечений отсчитываем от начала бомбиниро-ванного участка.

Для цилиндрического ролика (рис.1) R i i = D w/ 2             .

Здесь D_w – номинальный диаметр ролика.

Для ролика с радиусной бомбиной получим:

D w   ^{( l}p - ¹ф - x \¹ф - x )

2        2Rф при 1ф > x > lp - 1ф;

^R1i = "w^ при ¹ф <  x <  l p - ¹ф .

Для ролика с логарифмическим профилем бомбины получим:

D w         x + I T

¹ i = T ⁺ a ^{ф ln} i_ф + i_T ^при x - ¹ф ^;

R i i = ™ при ¹ф <  x <  ^lp ^{- 1}ф ;

D        l p + I t — x

R ^U = ^ ^{+ а} ф ^ln 1 ф + i T при x >  ^lp ^{— 1}ф .

Радиус наружного кольца во всех сечениях определяется по формуле:

R2н =(dm + Dw )/2.

Радиус не профилированного внутреннего кольца постоянный для всех сечений и определяется по формуле:

Здесь D_w - номинальный диаметр ролика, d_m – средний диаметр подшипника.

Для кольца с радиусной бомбиной получим:

R = d m - ^D w 2 вi           ₂

при ¹ф >  ^x >  ^lp ^{— 1}ф ;

^А к ^p ^{— 2} x ) 2 ^{— l}C ) W—lF)

^R 2 Bi = "^;-- w при ¹Ф <  x <  ^lp - ¹Ф .

Для кольца с логарифмическим профилем бомбины получим:

R. .

2 вi

dm ^{— D}w , ₇   /„ x ^{+ 1}Фк ^{+ l}Tк - ¹Ф

2      ⁺ a Фк I

2                      1Фк + lT к при x < 1ф ;

^R 2 в- = m^.—w при ¹ф <  x <  ^lp ^{— 1}ф ;

_ d m ^{— D} w._n ^lk ^{+ + 1}Tk - ¹Фк ^{+ 1}Ф - x

=     2     ^{+ а}Фк^ln      I +/

2                     1Фк + lTK при x > lp — 1ф .

Зазор z i между профилями ролика и кольца при перекосе определяется, как показано на рис. 3. При этом x ₀ – координата точки, в которой z = 0 при § = 0 , т.е. условной точки поворота ролика, зависит от формы ролика.

Зазор между профилированными поверхностями ролика и кольца может быть определен по формуле:

^zi = ^R 0 ^{— R} 1 i ^{+ R} 0 к ^{— R} 2 Bi ^{+ (} x ^— x 0 ) ^ в .

Здесь R ₀ и R _{0 к} - радиус ролика и внутреннего кольца в сечении с координатой x ₀ .

Координату x0 определим из условия ®кх + ® рх = ®в , где ®кх и 0рх - углы между общей касательной к профилям кольца и ро- лика и осями кольца и ролика соответственно, 0в - угол перекоса ролика относительно оси внутреннего кольца.

Для не профилированных ролика и кольца x ₀ =0 при любом значении угла перекоса ролика относительно кольца. Радиус ролика в точке с координатой x ₀ равен R ₀ = D _w 2 , радиус кольца в этой точке равен R 0 _к = ( d m — D w )/ 2 .

Для роликов и колец с криволинейной бом-

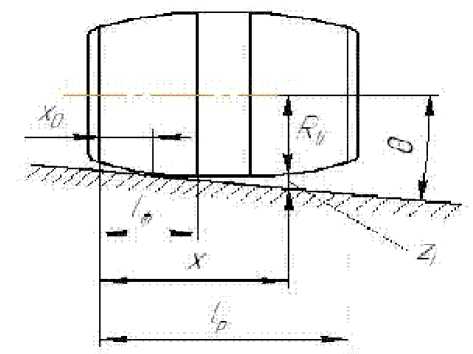
Рис. 3. Схема перекоса ролика относительно кольца

биной предельные значения углов поворота относительно кромки цилиндрического участка будут равны углам 0 и 0 наклона касатель-кр ной к соответствующей кривой в точке перехода к цилиндрическому участку.

Для роликов и колец с радиусной бомбиной при X = фф имеем: 0 р * Ф _с ( 2 R _ф ) и ⁰ к * ^ф с /⁽ 2 R фк ) . Тогда при ⁰ , <  ⁰ к ^{+ 0} р координата условной точки поворота ролика, определится как X о = Ф ф . Радиус R ₀ ролика в точке с координатой x ₀ равен D _w 2 , радиус кольца в этой точке равен R о к = ( d m - D , )/ 2 . При 0 , >  ⁰ к + ⁰ р углы наклона общей касательной к осям ролика и кольца в точке с координатой x ₀ будут равны:

• ⁰    рх * ^{( ф} с /^{2 + ф} ф ^- х о )/ R ф — для ролика;

• ⁰ кх * ^{( ф}с /^{2 + ф}ф ^- х о )/ R к — для кольца.

Из условия 0 кх + 0 _рх = 0 _в после подстановки и преобразований получим:

X о = Ф р /2 - R x о • 0 , .

Здесь: 1р = Фс + 2 Фф - расчетная длина ролика; RXо = Rф • Rк /(Rф + Rк ) - приведен- ный радиус кривизны профилей ролика и кольца.

Для роликов и колец с логарифмической бомбиной при X = Ф ф имеем:

⁰ р = ^аф ^{( ф}фф ^{+ Ф}Т ) ^{и 0} к = ^афк ( фк ^{+ Ф}Тк ^{) .}

Тогда при 0 _в <  0 _к + 0 р координата условной точки поворота ролика, определится как X о = Ф ф . Радиус R о ролика в точке с координатой x ₀ равен D _w 2 , радиус кольца в этой точке равен R о к = ( d m - D , )/ 2 . При 0 , >  0 к + 0 р углы наклона общей касательной к осям ролика и кольца в точке с координатой x ₀ будут равны:

• ⁰    рх = a ф ⁽ х^х о ^{+ ф} т ) - для ролика;

• ⁰ кх = ^афк /^{( X} о ^{+ Ф}фк — ^Фф ^{+ Ф}Тк ) ^- для кольца.

Из условия 0 кх + 0 _рх = 0 _в после подстановки и преобразований получим уравнение второго порядка:

0,хо + а1 хо + а 2 = о.

Здесь:

По условию совместности перемещений ве- личины деформаций в контактах в сечениях вдоль образующей ролика определяются по зависимости §i= 5о - zt, где §о — контактная деформация в точке с координатой x0 . По величинам деформаций определяются нагрузки в контактах в каждом сечении. При этом перекосы ролика относительно колец будут определяться условиями равновесия его под действием нагрузки, распределенной по линиям контакта и центробежной силы ролика.

С другой стороны по аналогии с гипотезой Винклера о пропорциональности деформаций нагрузкам в данной точке приближенно деформации в каждой точке линии контакта можно определить по формуле:

5t = 2Ft (at + a,i Ип • Аф).

bt = 27F, (n + П, )Rпр^™ • Лф).

Здесь П и П , - характеристики модулей упругости, определяемые по формулам:

П = ^{( 1 - е 2} У Е и П , = ^{( 1 -} е , )/ Е , , где E и E , - модули упругости, е и е , - коэффициенты Пуассона для материалов кольца и ролика соответственно.

При этом условие равновесия ролика в контакте можно написать в виде:

n

F„ =L F.

i = 1

Здесь F_n – нагрузка в контакте ролика с кольцом.

Решение приведенной системы уравнений выполняется численно последовательными приближениями. В качестве начального приближения принимается

• ⁵ о = ^{2 F}n ⁽ a о ⁺ a , о V^{( n} • ^ф, ) .

Здесь: a о = П(Фп (2 R 2о /Ьо)+ о,4о7),а, о = П, (Фп (2 R^ /Ьо )+ о, 4о7 ),

Ьо = 2 7 F. (П + П, )R „р о (П •ф, ) . Rro

– радиус ролика, R ₂₀ – радиус кольца и R_{пр 0} – приведенный радиус кривизны в точке с координатой х ₀ .

Для всех точек линии контакта ролика с кольцом определяются величины z. и 5 , по приведенным выше формулам.

При 5 , <  0 принимается F i = 0. иначе значение нагрузки определяется методом простой итерации по формулам:

bi = 2 VF0(П + V» )Rпр,/(п ■ Al);

В качестве начального приближения принимается F 0 = Fn/n . Если относительная погрешность I ( F , — F , )/ F ,\ превышает заданную величину, принимается F ₀ = F , и расчет повторяется.

Условия равновесия сил, действующих на ролик, имеют вид:

Fh = Fb + Fc.

При этом усилие в контакте максимально нагруженного ролика с внутренним кольцом определим по формуле: F . = 4 . 6 F r / z .

Усилие в контакте с наружным кольцом будет равно: F _h = F _b + F c .

Приведенный модуль упругости определим по формуле:

Е

прв

п

(1 — 8B )/Ев +(1 — eW )/Ew

контакта с внутренним кольцом;

E прн

П

1 — ^

н

– для

– для

I/Ен +(1 — 8, )/ E,

nn

E F^x, = E F₆iXi + F_c F /2 н            в        cp ^.

i = 1                    i = 1

Здесь: F _в и F_н – нормальные нагрузки в контактах ролика с внутренним и наружным кольцами, F _в и F_н – значения нагрузок в точках с координатами x .

При относительном перекосе колец 0 значения перекоса ролика относительно внутреннего и наружного колец определяются из решения приведенной системы уравнений равновесия ролика методом хорд. В качестве начального приближения принимается перекос ролика относительно внутреннего кольца 0 в = 0 /2 . Вычисляется значение перекоса ролика относительно наружного кольца 0 _н = 0 — 0 в . По приведенной ранее методике определяются нагрузки F_в

и Fн

и моменты

nn

Е ^F в, x , и Е ^F н, x , .

i = 1                  , = 1

Условие равновесия ролика проверяется по соотношению:

n

Е ^F н, x i - i = 1

n

Е Fв^^ДF c l p /2) — 1

< 0 . 001 .

При невыполнении условий равновесия уточняется значение 0 . и расчет повторяется.

В качестве критерия оптимизации профиля бомбины примем условие: напряжение на кромке ролика (сечение 1) при перекосе не должно превышать среднее значение контактных напряжений, определяемое по известным зависимостям [8] без учета перекоса колец:

1 F Е в прв

^О вт = F ЛГ/ R — для контакта с внут- ^п \ ^l Р R прв

ренним кольцом;

^а нт

п

F F н прн

I R p прн

– для контакта с на-

ружным кольцом.

контакта с наружным кольцом.

Приведенный радиус кривизны определим по формуле:

R прв = D , ( 1 — у )/2 - для контакта с внутренним кольцом;

R _прн = D , ( 1 + Y )/ 2 — для контакта с наружным кольцом.

Здесь у = D ,/ d m .

Для определения величин бомбины для ролика и для кольца составим уравнения:

U1 (A# .Aj= ^h (1)— Онт = 0 и

U 2 (A# .4,)-а. (1)— а.„ = 0.

Здесь а . ( 1 ) и а _н ( 1 ) - напряжения в сечении 1 у кромки ролика при перекосе.

Для решения полученной системы нелинейных уравнений применим метод Ньютона. При этом значения производных указанных функций определим как отношение приращений этих функций к приращениям аргументов.

В качестве начальных приближений аргументов 4 # и 4 к принимаем значения, при которых напряжения у кромки ролика больше нуля.

Обозначим начальные значения функций:

U10 = U1 (4#.4) иU20 = U2 (4.4к )■

Тогда приращения функций определим как разность:

U 1 # = U 1 ( 4 # + 44 ) — U 10 .

U2ф = U2(4# + 44 )— U20 .

U 1 , = U 1 ( 4 ф . 4 + 4 ) — U 10 .

U 2, = U 2 (4ф .4, + 4)—U 20.

Определитель системы найдем по формуле:

Opr = U1 ф • U2 к - U1 к • U2ф.

Уточненные значения величин бомбины ролика и кольца определим по формулам:

• 4.    = А к + ( U ,o • U 2ф - U 2o • U , ф ) ■ А Opr .

Процесс повторяется до достижения заданной точности вычисления критерия оптимизации, приведенного выше:

U1 (Аф,А,)= ан(1)-ант = 0 и

U2(Аф,.4,)- а,(1)-авт = 0.

В качестве примера рассмотрим результаты расчета межвального роликового подшипника 5-272822Р2 при следующих исходных данных: d = 110 мм, D = 140 мм, D_w = 8 мм, l_w = 10 мм, l c = 1 ^ 5 мм, I t = 0,5±0,2 мм, А ф = 0,002 ^ 0,012 мм.

Частота вращения внутреннего кольца n_в = 10200 об./мин., наружного – n_н = 13300 об./мин. Радиальная нагрузка на подшипник F_r =7 кН. Перекос внутреннего кольца относительно наружного принимался равным 0 =1 ^ 8 минут.

На рис. 4 приведены результаты расчета величины бомбины у ролика и у внутреннего кольца в зависимости от длины цилиндрического участка. Видно, что величина бомбины мало за-

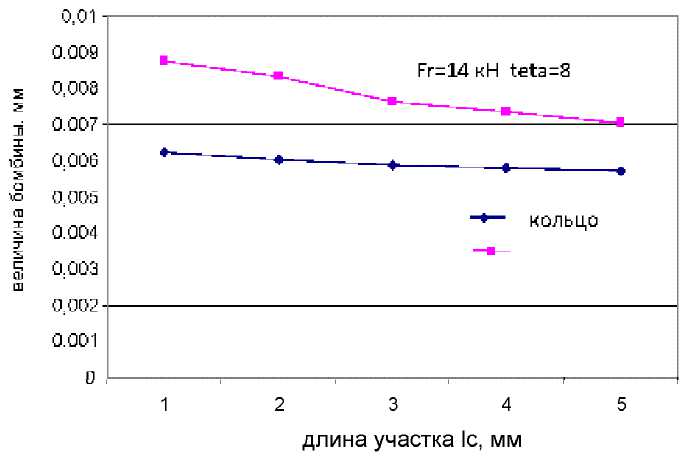
Рис. 4. Зависимость величин бомбины ролика и внутреннего кольца от длины цилиндрического участка

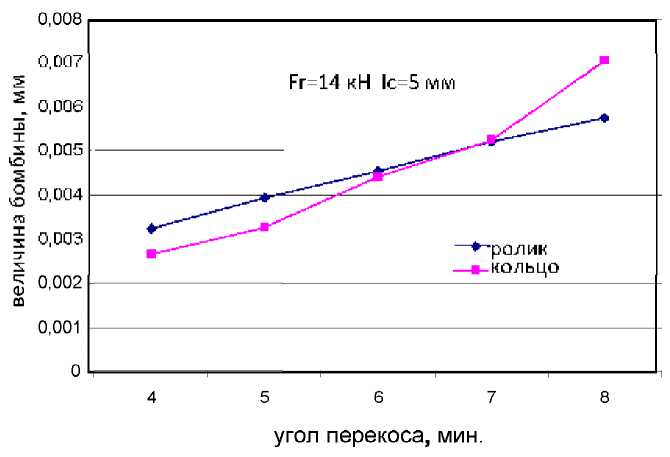
Рис. 5. Зависимость величин бомбины ролика и внутреннего кольца от угла перекоса колец подшипника

висит от длины цилиндрического участка профиля ролика и кольца.

Значительно более существенной является зависимость величины бомбины от величины угла перекоса колец, приведенная на рис. 5.

Таким образом, разработанная методика позволяет оптимизировать величину бомбины ролика и колец и, следовательно, повысить работоспособность подшипника при перекосе колец.