Оптимизация интерполятора многомерного сигнала в пространстве уменьшенной размерности

Объём обрабатываемых данных в настоящее время непрерывно увеличивается, зачастую растёт также и размерность этих данных, что естественным образом влечёт за собой необходимость решать различные задачи обработки многомерных сигналов [1].

Широко распространёнными примерами таких сигналов являются не только видео- [2], но также мульти- и гиперспектральные данные [3] (в том числе полученные в результате дистанционного зондирования Земли [4–5]). Такие данные могут содержать десятки и сотни спектральных компонент, благодаря чему обладают многими свойствами, присущими многомерным сигналам и массивам данных.

Задача интерполяции многомерных сигналов характеризуется достаточно большим количеством подходов к её решению, известных в настоящее время. Наиболее перспективными из них являются подходы, основанные на использовании искусственных нейронных сетей [6–7]. Наряду с ними, также быстро развивается подход на основе «compressed sensing» [8].

Чаще всего при решении прикладных задач, связанных с интерполяцией многомерных сигналов, используются подходы на основе метода опорных векторов [9], сплайнов [10] и обобщений метода наименьших квадратов [11]. В качестве менее распространенных подходов заслуживают упоминания тензорные интерполяторы [12], а также методы на основе Кронекеровских базисов [13] и локально оптимальных хорошо приспособленных базисных функций [14].

Наиболее важным достоинством упомянутых подходов является высокая точность интерполяции, по- тенциально достижимая при их использовании. Основным недостатком является их высокая сложность, препятствующая применению перечисленных решений в задачах, накладывающих существенные ограничения на вычислительную сложность. В таких условиях обычно используются какие-либо простые интерполяционные процедуры, основанные на линейных, билинейных или бикубических выражениях [15]. В противоположность перечисленным выше подходам эти простые выражения позволяют производить вычисления гораздо быстрее, но их точность невысока из-за отсутствия адаптивности.

В работах [16– 17] предложен подход к построению адаптивных параметризованных интерполяторов. Адаптивность этих алгоритмов основана на автоматическом переключении между простыми интерполирующими функциями в каждой точке сигнала. При этом использование быстрых вычислительных процедур на каждом этапе влечёт за собой низкую сложность алгоритма интерполяции в целом.

Однако с ростом размерности сигнала увеличивается также и размерность пространства параметров таких интерполяторов, что приводит к увеличению вычислительной сложности. В данной работе в рамках упомянутого подхода производится построение адаптивных параметризованных интерполяционных процедур, допускающих оптимизацию в параметрическом пространстве уменьшенной размерности. При этом производится именно снижение размерности пространства параметров адаптивного интерполятора, а не снижение размерности исходного сигнала.

Предложенные адаптивные интерполяторы многомерного сигнала могут использоваться при реше- нии различных прикладных задач обработки многомерных сигналов, таких как компрессия, совмещение разнородных сигналов и т.д.

В данной работе рассматривается применение адаптивных интерполяторов в задаче компрессии. Производится исследование эффективности адаптивных интерполяторов в рамках метода компрессии на основе иерархической сеточной интерполяции на реальных многомерных сигналах различных типов.

1.    Адаптивный параметризованный интерполятор многомерного сигнала

Пусть x ( n ) - многомерный сигнал, а П - вектор его аргументов. Пусть отсчёт x ( n ) необходимо интерполировать на основе множества ближайших опорных отсчётов { x ( П + m ): m e © }. Здесь смещение m задаёт расположение опорного отсчёта относительно интерполируемого отсчёта, а © - множество этих смещений.

Пусть для интерполяции отсчёта x ( n ) используется одна из простых интерполирующих функций Y ⁽ i ) ({ x ( ^Я + )}: m i e © ), i - номер интерполирующей функции. Обозначим U ⁽ i ) ( n) значения этих интерполирующих функций:

U ⁽ i ) ( n ) = Y ⁽ i ) ( { x ( n + m ) : m e © } ) .

Выбор конкретного интерполирующего значения для каждого отсчёта производится с помощью параметризованного решающего правила F :

u ( n , Я ) = U ¹ i ⁽ ‘ ) ) ( n ) , i ( Я ) = F ( f ( n ) , Я ) , (1) где u ( n , t ) - конкретное интерполирующее значение, выбранное в точке n , Я - вектор параметров, f ( n ) -вектор локальных признаков, которые также вычисляются на основе опорных отсчётов { x ( ^Я + m ): m e© }.

Решающее правило является параметризованным: оно зависит от векторного параметра t . Этот параметр автоматически вычисляется (для каждого сигнала отдельно) в ходе оптимизации некоторого критерия, вид которого определяется прикладной задачей. В качестве критерия может выступать, например, критерий минимизации абсолютных значений постинтерполяционных остатков:

^z(Я) = £|х (Я, Я)1 ^ min, (2) ЯеП t где Q - это множество всех возможных индексов (аргументов) исходного многомерного сигнала, а X (n, t) -собственно постинтерполяционные остатки

X ( n , Я ) = x ( n ) - u ( n , Я ). (3)

Этот критерий может использоваться при решении широкого круга задач, в частности, для совмещения разнородных сигналов [1], отличающихся количеством компонент и разрешением.

Кроме приведённого критерия, можно также использовать критерий минимизации энтропии [18] постинтерполяционных остатков, наиболее адекватный задаче компрессии, так как энтропия является хорошей оценкой объёма сжатых данных.

При использовании такого «энтропийного» критерия следует учесть, что во многих методах компрессии, в частности дифференциальных [19] и иерархических [20–21], постинтерполяционные остатки перед статистическим кодированием квантуются. Для определённости в данной работе при квантовании используется алгоритм квантования с равномерной [18] шкалой:

q ( n , Я ) = sign ( X ( n , Я ) )

^{X ( Я} , t ) + E max

2 s

max

+ 1

где e _max - вносимая при квантовании максимальная [15] погрешность (параметр квантователя), q ( ^Я , Я ) -квантованные постинтерполяционные остатки, а оператор [..] производит выделение целой части числа.

Во введённых обозначениях критерий минимизации энтропии H может быть записан в виде:

Q - 1

^{H (Я}) =^- Е ^Nq ^{(Я)1П N}q ^(Я) ^ min’            ⁽⁵⁾

q=- Q+1                              t где Nq (t)– количество квантованных постинтерполяционных остатков, имеющих   значение q, а Q = max(q(n, Я)) - максимальная величина постин-n терполяционного остатка (относительно небольшая величина, обычно существенно меньшая максимального значения исходного сигнала).

2.    Уменьшение размерности параметрического пространства

Для уменьшения вычислительной сложности при интерполяции часто используются алгоритмы [1,15], основанные на усреднении (сглаживании) по набору соседних опорных отсчётов:

u ( n ) = Е x ( n + m ^)/1®1 ,                           (6)

me© где мощность множества |©| фактически задаёт количество опорных отчётов (здесь и далее в целях упрощения изложения для величин u, q, i опускается зависимость от параметра t ).

Область расположения этих опорных отсчётов определяется прикладной задачей, и в некоторых случаях, например при дифференциальной [19] и иерархической [20– 21] компрессии, эта область может быть разрывна и иметь весьма нетривиальную форму (см. далее).

Сглаживающий интерполятор относительно точен внутри плавно изменяющихся областей сигнала, так как усреднение уменьшает неизбежно присутствующий шум. Однако для такого интерполятора всегда проявляется рост ошибки интерполяции на границах плавно меняющихся областей. Для интерполяции таких границ лучше работают нелинейные алгоритмы, использующие интерполяцию «в направлении» этих границ, игнорирующие «мешающие» отсчёты, принадлежащие соседним плавно изменяющимся областям. Для 2D-сигнала так работает, например, интерполятор Грэхема [22] и его обобщения, например интерполятор, инвариантный к двумерным границам четырёх направлений [15]. Естественно, на плавно изменяющихся участках сигнала такие нелинейные алгоритмы работают менее точно.

В данной статье используется подход к построению адаптивных параметризованных интерполяторов, совмещающий преимущества «усредняющего» и «нелинейного» подходов. Адаптивный интерполятор автоматически переключается между «сглаживающей» и «нелинейной» интерполяцией в зависимости от того, насколько сильно выражена граница плавно меняющихся областей в малой окрестности обрабатываемого отсчёта.

Пусть N c – количество принимаемых во внимание направлений границ областей (оно часто не совпадает с количеством опорных отсчётов). Пусть { 5 ⁽ c ) ( n ): 0 <  c < N_c } – множество абсолютных значений разностей

8 ^{( c} ) ( n ) = | % ( n + £ ) - x ( n + t)| (7)

между опорными отсчётами x ( n + У, x ( n + т ) в каждом из рассматриваемых направлений ( c – номер возможного направления границы).

В качестве опорных отсчётов x ( и + £ ), x ( n + т) обычно используются отсчёты, расположенные близко к интерполируемому отсчёту x (и) . Конкретная схема расположения опорных отсчётов зависит от прикладной задачи, в рамках которой используется интерполяция. В частности, при компрессии сигнала множество доступных опорных отсчётов определяется порядком обхода сигнала при обработке, который, в свою очередь, зависит от используемого метода компрессии. В следующих параграфах статьи схема расположения опорных отсчётов конкретизируется для интерполяторов в рамках иерархических методов компрессии [20 – 21].

Величины разностей 8 ^{( c} ) (Я) характеризуют наличие и степень выраженности границы областей в локальной окрестности отсчёта n . Для определения наличия и направления этой границы нужно использовать как минимум N c штук параметров t ^{( c )} , с которыми сравниваются разности 8 ^{( c} ) . Если в окрестности отсчёта граница отсутствует, то все разности 8 ^{( c} ) имеют близкие значения и используется «сглаживающая» интерполирующая функция вида (6):

и (Я) = U ⁽¹⁾ (Я) = £ x (Я + m )/|©| . (8) т е©

Если же в локальной окрестности отсчёта есть граница, то соответствующие ей разности 8(c) заметно отличаются от остальных, а для интерполяции ис- пользуется усреднённое значение и(j)(n) ближайших опорных отсчётов, расположенных в направлении этой границы (j – номер этого направления):

и (Я) = U ⁽²⁾ (Я) = и ^{( j )} ( И) .                               (9)

Таким образом, выражения (8, 9) задают значения интерполирующих функций U ⁽ i ) ( ^Я ) адаптивного интерполятора вида (1), а параметры t ( c ) , с которыми сравниваются разности 8 ^{( c} ) , составляют вектор параметров t решающего для правила этого интерполятора. Следовательно, для поиска наилучших значений параметров t ^{( c )} необходимо решать оптимизационную задачу вида (2) или (5) в N c -мерном пространстве параметров t ^{( c )} .

Размерность N c параметрического пространства определяется прикладной задачей и с увеличением размерности сигнала быстро растёт, так же как и вычислительная сложность оптимизации интерполятора, которая производится в этом пространстве параметров. При ограничениях, характерных, например, для многих приложений компрессии, вычислительная сложность может стать неприемлемой уже для случаев двух- или трёхмерного сигнала.

В данной работе вместо многопараметрического интерполятора (8, 9) предлагается использовать адаптивный параметризованный интерполятор многомерного сигнала, включающий процедуру оптимизации в параметрическом пространстве уменьшенной размерности.

Решающее правило этого интерполятора при выборе конкретной интерполирующей функции опирается не на абсолютные значения разностей 8 ^{( c} ) , а на их соотношения, которые удобно анализировать с помощью дополнительной ранговой [22] фильтрации этих разностей.

Построим вариационный ряд [22] разностей 8 ^{( c} ) ( ^Я ) и перенумеруем разности внутри него:

8^{( 0 )} ( n ) < 8^{( 1 )} (Я) < 8^{( 2 )} ( n ) < .. < 8⁽ N c ^{- 1 )} ( n ).

Для анализа этого вариационного ряда можно использовать различные ранговые фильтры, так или иначе обнаруживающие «существенно отличающиеся» от остальных группы разностей 8 ^{( c} ) , соответствующие преобладающим направлениям локальных границ областей. Рассмотрим наиболее простой из таких фильтров.

При построении интерполятора используются предположения, что если в окрестности текущего отсчёта сигнала нет границы гладких областей сигнала (или эта граница слабо выражена), то значения всех разностей 8 ^{( c} ) примерно одинаковы. Если же в этой окрестности есть достаточно выраженная граница, то разность, соответствующая направлению этой границы, будет минимальна, т.е. попадёт на первую пози-= ( 0 ) цию вариационного ряда 8⁽ ) .

При этом примерно одинаковы будут все остальные разности, и 8(0) будет существенно отличаться от них, в том числе от ближайшей к ней разности 5(1). Таким образом, характеристики вариационного ряда разностей 5(c) могут служить признаками направления и выраженности границы гладких областей сигнала в локальной окрестности текущего отсчёта. Самой простой из таких характеристик является разность между первыми двумя отсчётами вариационного ряда f (Я) = 5(1) (Я) -5(0) (Я) ,

которая в данной работе используется для определения наличия локальной границы и играет роль признака f (Я) в правиле (1) выбора интерполирующей функции каждого отсчёта.

Если признак (10) достаточно мал (меньше порога t), то в окрестности текущего отсчёта границы нет, и используется «сглаживающая» интерполяция вида (8). В обратном случае производится интерполяция вида (9) «вдоль» направления, соответствующего минимальной из разностей 5(c):

U ^{(1) ( Я )} = Z x ^{( Я} + m V©I , f ^{( Я ) -} t , I m e©

u ( ^Я ) = U ^{( 2 )} ( Я ) = u ⁽ j ) ( Я ), j = argmin{ 5 ⁽ c ) },            (11)

c t f (Я) > t.

Таким образом, размерность пространства параметров адаптивного интерполятора уменьшена до единицы: интерполятор (11), в отличие от схемы (8, 9), является однопараметрическим (с единственным скалярным параметром t ), что существенно упрощает его оптимизацию.

• 3.    Оптимизация адаптивного интерполятора

При оптимизации описанного выше адаптивного интерполятора многомерного сигнала рассмотрим критерии минимизации абсолютных значений (2) постинтерполяционных остатков и энтропии (5) квантованных постинтерполяционных остатков.

При минимизации показателя (2) используется вспомогательный двумерный массив Л , элементы которого вычисляются следующим образом:

^л / , ф = Z I ^{х ( Я )} - U ^{( i )( Я )}|,

Я: f (Я )=ф i e{1,2}, фе[0..M -1],                            (12)

M = max( x ( ^Я )).

Я

Элемент Л ₁ , ф этого массива содержит сумму модулей постинтерполяционных остатков интерполирующей функции U ^{( i )} , заданной одним из выражений (11), для отсчётов со значением признака (10), равным ф .

На основе статистики (12) значение Х е ( t ) показателя (2) для всех значений порога t вычисляется рекуррентной процедурой:

M - 1

Хе( m ) = £ль f, f=0

Х_е ( t ) = х_е ( t + 1 ) + Л ₂, t -Л 1, t , 0 - t <  M .

Оптимальное значение параметра topt = argmin Хе (t), которое можно найти перебором в коротком массиве Хе (t) длины (M+1), является решением оптимизационной задачи (2).

При минимизации энтропии (5) квантованных постинтерполяционных остатков (4) собирается трёхмерная статистика:

N f ) q , i e { 1,2 } , 0 - f <  M , - Q <  q <  Q , Q = max( q ( ^Я )).

Я

Элемент N ⁽ _f ⁱ _, ⁾ _q содержит количество отсчётов квантованных постинтерполяционных остатков (4), имеющих значение q , при значении признака (10), равном f , при использовании интерполирующей функции U ^{( i )} , которая задаётся одним из выражений (11).

Статистика N ⁽ _f ⁱ _, ⁾ _q используется рекуррентной процедурой вычисления количества N q ( t ) значений квантованных постинтерполяционных остатков, равных q, при всех значениях параметра t :

M - 1

N, ( 0 ) = EN?),, q ’ ^Z f ■ q                                  (15)

N q ( t + 1 ) = N q ( t ) - N (1 q + N (2) ,0 - 1 <  M .

Статистика Nq (t) даёт возможность вычислить энтропию H (t) квантованных постинтерполяционных остатков при всех значениях порога t с помощью выражения (5). Индекс минимального значения topt = arg min H (t), который можно найти перебором в коротком массиве H (t) длины M, является решением оптимизационной задачи (5).

• 4.    Адаптивная интерполяция при иерархической компрессии

В данной работе также рассматривается применение адаптивного интерполятора многомерных сигналов в задаче иерархической компрессии [20, 21], при решении которой используется безызбыточное представление (см. рис. 1, 2) исходного многомерного сигнала X = { x (Яг)} в виде иерархического набора из L масштабных уровней X l :

L - 1

X = U X 1 , X 1 = { X i ( Я ) } = { X ( ^Я ): я e I_t } ,         (16)

1 = 0

где множество I l задаёт индексы отсчётов масштабного уровня X l :

I, . = ( 2 L ^{- 1} Я\ , I, =( 2 Я \(2 ^{1 + 1} Я),0 - 1 <  L . (17) L - 1                        1

Таким образом, наиболее прореженный масштабный уровень XL–1 представляет собой исходный сигнал, прореженный с шагом 2(L –1). Любой из остальных масштабных уровней номер l = (L-1)..0 представляет собой прореженный с шагом 2l сигнал, из которого исключены отсчёты прореженного с шагом 2l+1 сигнала.

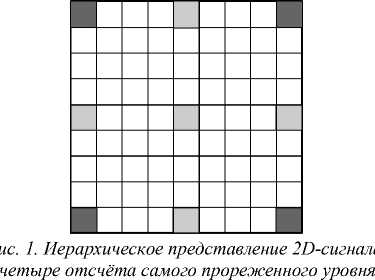
и пять отсчётов менее прореженного уровня

Разности 5 ⁽ с ) вида (7) в трёхмерном случае принимают вид:

5 1^е ) ( 2 m + 1,2 n + 1,2 к + 1 ) =

= x l _{+ 1} ( m + a , n + b, к + d ) - x l _{+ 1} ( m + a , n + b , к + d )| , (19)

е = a + 2b + 3d; abd = 000,100,010,001, где a = 1 - a обозначает логическое отрицание.

Значения интерполирующих функций (1) трёхмерного адаптивного интерполятора для отсчётов масштабного уровня X l могут быть записаны в виде:

U_; ⁽¹⁾ ( 2 m + 1,2 n + 1,2 к + 1 ) =

= ZZZ x ; + 1 ( m + a , n + b , к + d )/8, a = 0,1 b = 0,1 d = 0,1

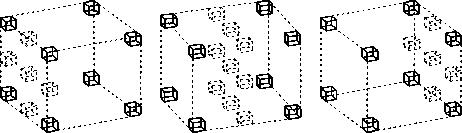
Рис. 2. Иерархическое представление 3D-сигнала: восемь отсчётов самого прореженного уровня и 19 отсчётов менее прореженного уровня, разнесённые на три отдельных рисунка

Нетрудно видеть, что описанное иерархическое представление безызбыточно:

X p П X z = 0V p * z .                      (18)

При иерархической компрессии масштабные уровни X l обрабатываются последовательно, в порядке ( L – 1), ( L – 2) .. 2, 1, 0. Отсчёты каждого уровня интерполируются на основе отсчётов менее прореженных уровней, постинтерполяционные остатки квантуются и кодируются энтропийным кодером (см. рис. 3).

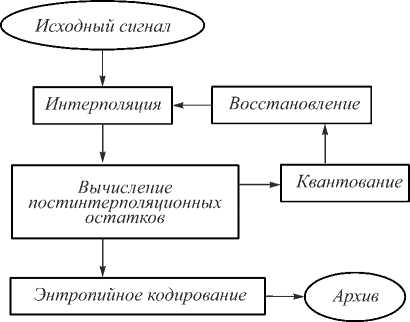
Рис. 3. Место интерполятора в структуре методов компрессии многомерных сигналов

Запишем в явном виде интерполирующие функции адаптивного интерполятора в трехмерном случае для отсчётов масштабного уровня X l с координатами вида n = 2 ¹ ( 2 m + 1, 2 n + 1, 2 к + 1 ) . При этом описанные ранее величины U ⁽ ' ) , 5 ⁽ с ) , u ⁽ j ) вычисляются отдельно на каждом иерархическом уровне номер « l » и далее помечаются дополнительным нижним индексом « l ».

U _; ^<2,( Я) = u l^(j ) (Я), j = argmin { 5 (f ) (Я) } ,              (21)

где

u ^{( е} ) ( 2 m + 1,2 n + 1,2 к + 1 ) =

= ( x l _{+ 1} ( m + a , n + b , к + d ) + x l _{+ 1} ( m + a , n + b , к + d ) ) /2, е = a + 2 b + 3 d ; abd = 000,100,010,001.

Выбор между значениями интерполирующих функций (20) и (21) в каждой точке сигнала автоматически производится с помощью решающего правила (11). Таким образом, трёхмерный адаптивный интерполятор в каждой точке переключается между «усредняющим» интерполятором (20) и интерполирующими функциями (21) «вдоль» четырёх направлений.

В двумерном случае значения интерполирующих функций адаптивного интерполятора записываются следующим образом:

U_; ⁽¹⁾ ( 2 m + 1,2 n + 1 ) = ( x l _{+ 1} ( m , n ) + x l _{+ 1} ( m + 1, n ) + + x l _{+ 1} ( m , n + 1 ) + x l _{+ 1} ( m + 1, n + 1 ) ) / 4,

U(2)(я) = /M^(n), 510)(n) "511)(Я), l (n)    [u®(я), 5(0)(я) >5;(1)(n),

где u|е) (2 m +1,2 n +1) =

= ( x l _{+ 1} ( m + a , n + b ) + x l _{+ 1} ( m + a , n + b ) ) /2,      (24)

е = a + b ; ab = 00,01.

а 5 1 ⁰⁾ ( n ), 5 ⁽¹⁾ ( ^я ) - разности вида (7), которые могут быть записаны в виде:

5 1^е ) ( 2 m + 1,2 n + 1 ) =

I x l _{+ 1} ( m + a , n + b ) - x l _{+ 1} ( m + a , n + b )|

е = a + b ; ab = 00,01.

Для выбора интерполирующей функции также используется решающее правило (11). Таким образом, двумерный адаптивный интерполятор, кроме «усредняющей» функции (22), использует также интерполирующие функции (23) «вдоль» двух направлений.

• 5.    Экспериментальное исследование адаптивного интерполятора

Для исследования эффективности адаптивного интерполятора в составе иерархического метода компрессии проведены вычислительные эксперименты на реальных многомерных сигналах двух типов:

• а)    сигналы гиперспектрометра AVIRIS [23] разме

  ра 1086 x 614 x 224 (16 бит);

• б)    гиперспектральный набор сигналов

«TokyoTech» [24] размера 500 x 500 x 31 (13 бит).

Также проведено сравнение адаптивного интерполятора с усредняющим интерполятором. В качестве меры эффективности адаптивного интерполятора ис- пользовался выигрыш А в объёме сжатых данных, который обеспечивался за счёт замены усредняющего интерполятора на адаптивный интерполятор в составе иерархического метода компрессии:

А= ( kjk_s - 1 ) - 100% , (26) где k s , k a – коэффициенты компрессии при использовании усредняющего и адаптивного интерполятора.

Типичные примеры результатов вычислительных экспериментов, проведённых при различных значениях максимальной погрешности s max , показаны на рис. 4–7. Результаты подтверждают существенный (до 17 %) выигрыш адаптивного интерполятора.

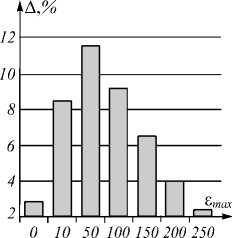
Рис. 5. Выигрыш адаптивного интерполятора на тестовом многомерном сигнале «Party» гиперспектрального набора «TokyoTech» (также показаны компоненты сигнала № 0, 10, 20, 30)

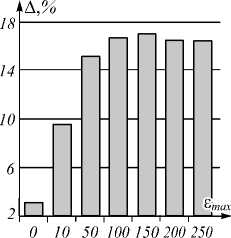
Рис. 4. Выигрыш адаптивного интерполятора на тестовом многомерном сигнале «Flower» гиперспектрального набора «TokyoTech» (также показаны компоненты сигнала № 0, 10, 20, 30)

Л,%

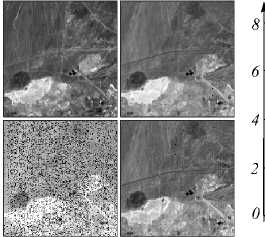
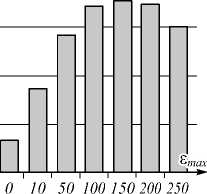
Рис. 6. Выигрыш адаптивного интерполятора на тестовом многомерном сигнале «Cuprite» гиперспектрометра AVIRIS (также показаны фрагменты компонент сигнала № 10, 86, 100, 120)

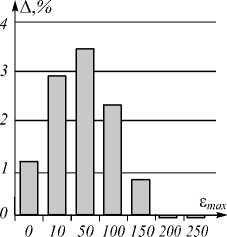
Рис. 7. Выигрыш адаптивного интерполятора на тестовом многомерном сигнале «Low Altitude» гиперспектрометра AVIRIS (также показаны фрагменты компонент сигнала № 2, 70, 121, 157)

Заключение

Исследовались адаптивные алгоритмы интерполяции многомерных сигналов в рамках решения задачи иерархической компрессии сигналов. Адаптивность рассмотренных алгоритмов основана на выборе интерполирующей функции в каждой точке сигнала с помощью параметризованного решающего правила, оптимизация которого производится в пространстве уменьшенной размерности. Проведены вычислительные эксперименты на реальных многомерных сигналах, подтверждающие преимущество адаптивного интерполятора, который позволяет существенно (до 17 %) повысить эффективность иерархического метода компрессии.

Исследование выполнено при финансовой поддержке РФФИ в рамках научных проектов

№ 18-01-00667, 18-07-01312, а также Министерства науки и высшего образования РФ в рамках Государственного задания ФНИЦ «Кристаллография и фотоника» РАН (соглашение № 007-ГЗ/Ч3363/26).