Оптимизация, изготовление и исследование кремниевой бинарной субволновой цилиндрической линзы терагерцового диапазона

Появление источников мощного терагерцового излучения, таких как лазеры на свободных электронах [1], привело к необходимости формирования элементной базы для управления характеристиками мощных пучков терагерцового излучения. Известны результаты исследования пропускающих [2–5] и отражающих [6] элементов, предназначенных для фокусировки мощного терагерцового пучка в заданные двумерные [4] и трёхмерные [7] области, а также для формирования мощных терагерцовых пучков с заданными поперечно-модовым составом [8] и поляризационным состоянием [9]. В качестве материала подложки пропускающих силовых терагерцовых эле- ментов в [2–5, 7–9] использовался высокорезистивный кремний [10]. В работах [5, 6] приведены результаты исследования пропускающей кремниевой цилиндрической дифракционной линзы и отражающей цилиндрической линзы соответственно. Цилиндрические линзы играют большую роль при построении сканирующих терагерцовых систем. Пропускающие кремниевые линзы со ступенчатым рельефом могут быть изготовлены с помощью технологий литографии [2, 3] или технологии лазерной абляции [11]. Однако дифракционная эффективность бинарных (двухуровневых) линз с шириной зон Френеля, значительно превышающих длину волны, составляет всего 41 %, в то время как изготовление линз с большим количеством уровней («ступенек») рельефа и, соот- ветственно, большей дифракционной эффективностью с помощью литографических технологий требует применения дорогостоящей и сложной процедуры [12]. В качестве альтернативы технологиям литографии в работе [5] была рассмотрена технология лазерной абляции, позволяющая формировать непрерывный дифракционный микрорельеф на поверхности кремниевой подложки. Другим вариантом относительно недорогого изготовления линз с более высокой дифракционной эффективностью является оптимизация и изготовление субволнового бинарного дифракционного микрорельефа на поверхности кремниевой подложки.

Ранее были хорошо описаны теоретические подходы к решению задачи дифракции на субволновых бинарных структурах [13, 14]. Целью нашей работы является расчёт, изготовление и исследование методами численного и натурного экспериментов кремниевой цилиндрической дифракционной линзы с субволновым дифракционным микрорельефом.

1.    Постановка задачи

Рассматривалась работа бинарной цилиндрической дифракционной линзы (ДЛ), i -я дифракционная зона которой представлена на рис. 1.

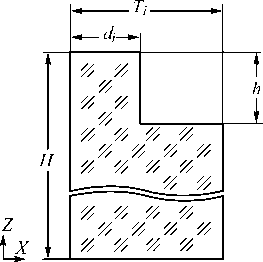
Рис. 1. Изображение i-й зоны ДЛ

На рис. 1 H – высота подложки, h – глубина травления штриха, d i – ширина штриха i -й зоны, T i – ширина i -й зоны. Известно [13, 14], что при падении света под углом а = 30° на бинарную дифракционную решётку с периодом штриха, приблизительно равным λ, среди прошедших дифракционных порядков остаются только 0 и –1, а остальные являются быстро затухающими. Таким образом, в качестве целевой функции будем использовать значение дифракционной эффективности в минус первом порядке для таких зон. Параметрами оптимизации выберем коэффициент заполнения штриха ff i и глубину травления штриха h . Коэффициент заполнения ff i определим как отношение ширины штриха d i к ширине зоны T i : ff i = d i / T i .

Если считать, что каждая отдельная зона ДЛ будет иметь свою глубину травления и коэффициент заполнения, то конечная задача будет иметь высокую вычислительную сложность. Увеличение вычислитель- ной сложности приведёт к быстрому росту временных затрат на вычисления. Кроме того, такой микрорельеф уже будет невозможно реализовать с помощью однократного литографического травления подложки [12]. Поэтому ограничивались целевой функцией, которая зависела всего от двух переменных – коэффициента заполнения и глубины травления. Эта пара параметров предполагалась одной и той же для всех зон ДЛ. Выбранный размер бинарной структуры, состоящей из набора зон рис. 1, вдоль оси х составлял 50 мм. Высота подложки составляла 1 мм. Длина волны падающего излучения выбиралась равной λ = 141 мкм. В качестве материала ДЛ выбирался высокоомный кремний с показателем преломления n = 3,42. В качестве освещающего пучка рассматривался Гауссов пучок, падающий на плоскость ДЛ под углом а = 30°. Предполагалось, что плоскость фокусировки должна располагаться в f =300 мм от линзы в –1 порядке дифракции.

2.    Численный эксперимент

Перед началом численного эксперимента было необходимо выбрать начальное приближение для параметров ДЛ и определить ширину зон линзы. В работах [15, 16] описаны подходы для расчёта ширины зон. В качестве значений начальных параметров выбирались h = 0,25λ и ff = 0,5.

Ширина зоны должна удовлетворять уравнению [16]:

ф ₀ + к 0 V Т П2 + f ² + 2 к 0 sin ( а ) T n = 2 п n , (1)

где φ 0 – начальная фаза эйконала, k 0 – волновое число, T n – координата границы зоны с индексом n , f – фокусное расстояние, а - угол падения пучка, n - номер зоны. Для расчета ДЛ использовалась функция оптимизации fmincon, реализованная в среде MATLAB.

В результате работы оптимизационной процедуры было найдено решение, соответствующее значению дифракционной эффективности элемента e =70% (определяется как величина падающего потока, который дифрагирует в заданном порядке дифракции). Полученные значения параметров при этом составили h =63 мкм, ff = 0,3. Работа линзы оценивалась с помощью метода локальной аппроксимации [16]. Для обозначенных выше параметров распределение модуля вектора Умова–Пойнтинга в области фокуса имело вид, приведённый на рис. 2. Асимметрия фокального распределения (рис. 2) обусловлена тем, что пучок падает на ДЛ под углом. ДЛ состояла из 320 зон.

Зависимость дифракционной эффективности минус первого порядка от ширины зоны представлена на рис. 3. На рис. 3 вдоль оси Х отложены значения ширины i -й зоны ДЛ в длинах волн (λ = 141 мкм).

Видно, что для параметров, полученных в результате оптимизации, дифракционная эффективность практически не опускается ниже e =60% и возрастает по мере увеличения ширины зоны, составляя в среднем e =70%. Однако полученные позже результаты экспериментального исследования рассчитанной и изготовленной линзы показали значительно меньшее значение измеренной дифракционной эффективности. Было сделано предположение, что основной причиной сильного снижения дифракционной эффективности является деструктивная интерференция в объёме оптически плотной пластины из кремния, толщина пластины никак не учитывалась в ходе расчёта ДЛ.

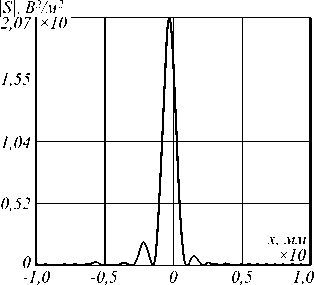
Рис. 2. Модуль вектора Умова–Пойнтинга в фокальной области бинарной дифракционной линзы

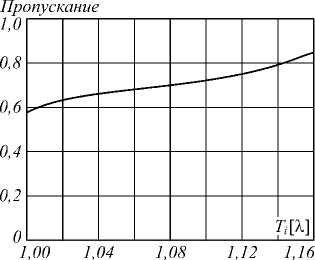
Рис. 3. Зависимость дифракционной эффективности минус первого порядка от ширины зоны

Для оценки снижения дифракционной эффективности был поставлен численный эксперимент, в ходе которого рассматривалась ДЛ с выбранными параметрами рельефа. Начальная толщина подложки составляла 1 мм, исследовалось изменение дифракционной эффективности при отклонении от этой толщины в пределах ± 10 мкм. Это отклонение соответствует ширине области определения параметра высоты рельефа решётки, при котором эффективность всё ещё больше 20 %. Так, при увеличении толщины, как и при её уменьшении (рис. 4), наблюдается многократное падение дифракционной эффективности.

3.    Натурный эксперимент

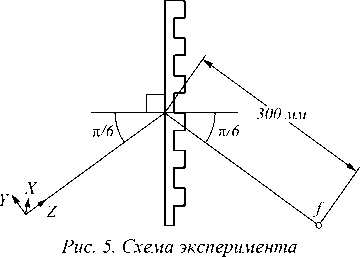
Изготовление субволновой цилиндрической линзы с найденными параметрами осуществлялось методом плазмохимического травления (Бош-процесс) поверхности подложки из высокоомного кремния [3]. Параметры элемента – апертура D =50 мм, рабочая длина волны X = 141 мкм, угол падения освещающего пучка - а = 30°, тип микрорельефа - бинарный субволновый. Расчётная высота микрорельефа – h =63 мкм, ширины зон менялись в диапазоне от λ до 1,16λ. Фокусное расстояние линзы f =300 мм. Из-за большой глубины травления имело место подтравли-вание стенок микрорельефа. По результатам исследования получившегося микрорельефа методом микроинтерферометрии (использовался микроинтерферометр белого света WLI-DMR производства Института Фраунгофера, г. Йена, Германия) величина угла под-травливания составила примерно 13°. Для оценки параметров реальной ДЛ с наклонными стенками использовался метод [5]. Оказалось, что для изготовленной ДЛ дифракционная эффективность из-за подтрава должна снизиться приблизительно на 5%. Изготовленный субволновый элемент исследовался методами натурного эксперимента. В качестве источника когерентного терагерцового излучения использовался Новосибирский лазер на свободных электронах (НЛСЭ, ИЯФ СО РАН) [1]. Схема эксперимента показана на рис. 5. Длина волны составляла X =140,6 мкм (по монохроматору НЛСЭ). Излучение падало под углом 30° к нормали поверхности элемента со стороны гладкой (без микрорельефа) поверхности. Толщина кремниевой подложки, на которой находился реализованный профиль, отличалась от расчетного значения, использованного выше в модельном примере (1 мм), и составляла 0,96±0,01 мм. Для длины волны X =141 мкм излучение должно собираться в фокусе f=300 мм под углом а = 30°. Для наблюдения профиля пучка использовался матричный пироэлектрический приёмник Pyrocam IV, а поляризация на входе задавалась фотолитографическим плёночным поляризатором. Во всех измерениях вектор напряжённости электрического поля падающего излучения был параллелен штрихам решётки.

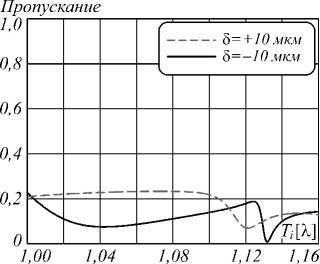
Рис. 4. Зависимость дифракционной эффективности минус первого порядка от ширины зоны при увеличении толщины кремниевой пластины на ± 10 мкм

Расстояние от места падения пучка на линзу до области с максимальной энергией фокуса составило примерно 295± 10 мм, что находится в хорошем соответствии с расчётным значением. Небольшая точность экспериментального определения данного рас- стояния свидетельствует о большой длине каустики фокуса линзы. Ни рис. 6 показано изображение фокуса, измеренного на матричном приёмнике в данной геометрии при угле падения а = 30°. Фокус был немного наклонён к вертикальной оси (под углом примерно а = 9°). Возможно, это произошло из-за того, что вектор электрического поля был немного отклонён от линий штрихов элемента. В целом, это отклонение существенно не влияло на результат.

На рис. 7 показано изображение пучка, прошедшего напрямую через элемент (без отклонения от направления падающего пучка), а на рис. 8 – профиль падающего пучка. По измеренным распределениям интенсивности (рис. 6– 8) была оценена суммарная интенсивность фокального пятна If (по эллипсу с размером 3,4×24 мм2), прошедшего пучка It (по всей площади матрицы приёмника) и падающего пучка I0. Данные величины составили примерно If ≈ 35,6, It ≈ 113,7 и I0 ≈ 575,6 отн. ед. соответственно. Исходя из этих данных, была оценена энергетическая эффективность – как отношение If /I0 ≈ 6,2±0,5 %, а дифракционная эффективность, как If /(It + Ir) ≈ 24± 1 %, где Ir – суммарная интенсивность отражённого поля. Погрешность измерений составила ≈ 5 %, которая связана в значительной степени с колебаниями интенсивности падающего излучения ЛСЭ. Полученный результат для дифракционной эффективности согласуется с расчётами с учётом многолучевой интерференции в оптической системе линза–подложка (волновод) с толщиной подложки, отличающейся на 10 мкм от значения, при котором получены оптимальные параметры (см. рис. 4). Следовательно, основной источник значительного расхождения расчётной эффективности при оптимальных параметрах линзы (70%) с экспериментальным значением – деструктивная интерференция излучения в подложке (играющей роль волновода), на которой изготовлена кремниевая линза. Таким образом, при использовании описываемого подхода к расчёту пропускающих фокусирующих элементов необходимо дополнительно учитывать толщину подложки, используемой для изготовления элемента.

Заключение

Проведена оптимизация параметров бинарного субволнового микрорельефа цилиндрической ДЛ те-рагерцового диапазона. Для ДЛ с рабочей длиной волны X =141 мкм, фокусным расстоянием f =300 мм и расчётным значением угла падения освещающего пучка а = 30° глубина травления зон и коэффициент заполнения оказались равны соответственно h = 64 мкм, ff = 0,3. Рассчитанная дифракционная эффективность линзы с таким микрорельефом составила 70 %. Дифракционная линза была изготовлена с помощью технологии плазмохимического травления (Бош-процесс) поверхности подложки из высокоомного кремния. Изготовленный микрорельеф был исследован методом интерферометрии белого света. Было проведено численное моделирование сформированного микрорельефа с учётом имеющихся технологических погрешностей изготовления. Изготовленная ДЛ была исследована методом натурного эксперимента. В качестве источника излучения использовался Новосибирский лазер на свободных электронах (НЛСЭ).

Рис. 6. Профиль фокуса на расстоянии f = 295 мм (наблюдаемый под a = 30°); здесь и далее размер кадра равен

25,6×25,6 мм2

Рис. 7. Изображение пучка, прошедшего напрямую через элемент (без отклонения от направления

Рис. 8. Профиль падающего пучка ЛСЭ

падающего пучка)

Эксперимент продемонстрировал фокусирующие способности созданного элемента, экспериментальная оценка фокусного расстояния находится в хоро- шем соответствии с расчётным фокусным расстоянием. Однако экспериментальная оценка дифракционной эффективности была значительно меньше рас- чётной. Расхождение экспериментального и численного результата было в значительной степени обусловлено неравномерностью толщины кремниевой пластины. Такая неравномерность приводит к набегу фаз, пропорциональному 2π, которой, в свою очередь, может существенно снизить эффективность [17]. В статье приведён анализ снижения дифракционной эффективности, связанного с 1) технологическими погрешностями формирования дифракционного микрорельефа; 2) деструктивной интерференцией излучения в случае отсутствия учёта толщины кремниевой подложки при расчёте микрорельефа. Приведены рекомендации по расчёту микрорельефа с учётом толщины подложки.

Отметим, что обобщение описанного подхода на двумерный случай позволит решить задачу фокусировки лазерного излучения в двумерную область с помощью бинарного субволнового дифракционного оптического элемента.

Работа выполнена при поддержке Российского научного фонда (проект № 19-72-20202) на уникальной установке «Новосибирский лазер на свободных электронах» с использованием оборудования «Сибирского центра синхротронного и терагерцового излучения».