Оптимизация измерительных преобразователей на основе согласованной фильтрации и технологии поверхностных акустических волн

Математические модели согласованной фильтрации наиболее подробно рассмотрены в работе [1], а измерительные преобразователи на основе поверхностных акустических волн (ПАВ) — в работах [1, 2, 3]. Однако до настоящего времени отсутствуют публикации о применении методов согласованной фильтрации для синтеза структур различных измерительных преобразователей ПАВ в зависимости от их назначения и условий применения.

Задачей данной работы является разработка инженерных методов проектирования структур датчиков, реализующих согласованную фильтрацию ПАВ.

К проектированию ПАВ-датчиков предъявляется ряд требований, которые могут быть и противоречивыми, например обеспечение следующих характеристик:

• -    максимальная энергия выходного (переизлу-ченного) сигнала;

• -    максимальная чувствительность к изменению топологии (структуры) рабочей поверхности пьезоэлектрической пластины.

Эти и другие требования являются количественно неопределенными, однако они должны быть выполнены с учетом ограничений, лишь некоторые из которых известны до начала проектирования, например такие:

• -    максимальная импульсная мощность зондирующего сигнала передатчика не должна превышать 2 Вт;

• -    максимальная средняя мощность зондирующего сигнала передатчика не должна превышать 10 мВт;

• -    частоты сигналов должны принадлежать разрешенным диапазонам частот (433 - 434; 867 - 869; 905 - 926; 2410 - 2490) МГц;

• -    максимальная длительность запросного импульса ограничена потерями в звукопроводе и, как правило, не превышает 10 мкс.

Аналогичные требования необходимо предъявлять и к системам пассивной идентификации. Пассивные радиометки должны вносить минимальные потери в полученную от передатчика энергию. Возможна и другая интерпретация — минимальное уменьшение средней переизлученной мощности.

ОСОБЕННОСТИ СОГЛАСОВАННОЙ ФИЛЬТРАЦИИ В ЗАДАЧАХ

ИДЕНТИФИКАЦИИ И ИЗМЕРЕНИЯ

Акустоэлектронная радиометка, в рассматриваемом случае на ПАВ, является средством кодирования, т. е. видоизменяет принятую последовательность в переизлученную последовательность с минимальными потерями энергии. В простейшем случае радиометка переставляет элементы полученной последовательности в предопределенном порядке. Зная исходную последовательность и закон ее изменения (перестановки), можно реализовать согласованную фильтрацию переизлученной радиометкой кодовой последовательности (рис. 1).

Предложенная система идентификации на основе ПАВ-технологий полностью соответствует принципам линейной теории кодирования [4]. Для чувствительных элементов датчиков физических величин хорошую эффективность показала топология с дифференциальным дисперсионным преобразователем [5], которую иллюстрирует топо-

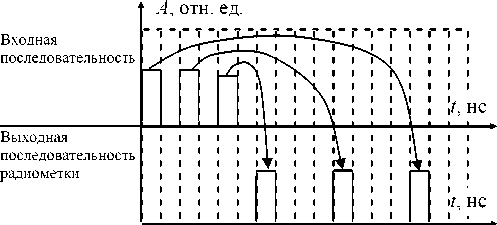
Рис. 1. Схема перекодирования сигнала радиометкой

2 N

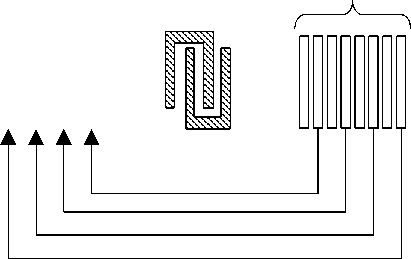
Рис. 2. Модифицированная топология дисперсионной линии задержки на ПАВ логия на рис. 2. Здесь отражающие структуры сгруппированы в 2N отражателей. Топология на рис. 2 в пределе позволяет изменить на π рад разность фаз смежных полупериодов.

МОДЕЛЬ ЧУВСТВИТЕЛЬНОГО ЭЛЕМЕНТА

В основу дальнейшего изложения положено известное представление выходного сигнала (отклика) в виде интеграла свертки

t

• x = j x 1 T ) x ₂( t - т )d T ,                (1)

где х — выходной сигнал измерительного преобразователя, x ₁ — зондирующий сигнал, x ₂ — импульсная переходная функция измерительного преобразователя, τ — аргумент интегрирования.

x ₂ ( t )

x 1 ( t - ф ) = sin( ® 1 t - ф )

x

ω ₂

p ² + ю ₂ ²

Рис. 3. Структурная схема преобразования входного сигнала ПАВ-датчиком

Из теории ПАВ известно, что зондирующий сигнал x1 и импульсная переходная функция x2 ПАВ-датчиков представляют собой гармонические функции, простейшими моделями которых могут служить синусоиды (косинусоиды), заданные на ограниченном интервале времени. Поэтому без ограничения общности при постановке задачи оптимизации можно принять представление зондирующего сигнала и импульсной переходной функции в виде синусоид x1 (t) = A s ln( ^1 т - ф); x2 (t) = sin(®21), (2) где А — амплитуда зондирующего сигнала, заданного на интервале Tx; ω1 , ω2 — круговые частоты зондирующего сигнала и импульсной переходной функции измерительного преобразователя соответственно; ϕ — сдвиг по фазе.

С учетом (2) модель выходного сигнала (1) ПАВ-датчика:

t x = Ajsin(^lr - ф)sin[^2(t - r)]dт . (3) 0

Из анализа простейшей модели (3) следует, что выходной сигнал ПАВ-датчика зависит от четырех величин: A , ω ₁ , ω ₂ и ϕ . В более сложных моделях указанные величины могут зависеть от таких параметров реализуемой структуры, как например периодичность, глубина, ширина и профиль элементов отражающих, измерительных и генерирующих структур, характеристики пьезоэлектрической пластины, по поверхности которой распространяются акустические волны, и др.

Модель (3) при постоянном фазовом сдвиге ϕ соответствует преобразованию сигнала в соответствии со структурной схемой рис. 3, где р — параметр преобразования по Лапласу импульсной переходной функции.

Источником энергии является зондирующий сигнал x ₁ ( t ) , который воспринимается измерительным преобразователем с импульсной переходной функцией x ₂ ( t ) , преобразующим зондирующий сигнал x ₁ ( t ) передатчика в выходной сигнал отклика х чувствительного элемента.

Возможны две постановки задачи оптимизации:

• 1)    найти зондирующий сигнал x ₁ ( t ) , обеспечивающий наибольшую энергию выходного сигнала х ;

• 2)    найти значения ϕ , обеспечивающие наибольшую чувствительность параметров выходного сигнала х к изменению фазового сдвига ϕ .

Известно [1], что наибольшая импульсная мощность выходного сигнала получается при импульсной переходной функции x ₂ ( t ) , согласованной с зондирующим сигналом x ₁ . Поэтому в общем случае необходимо определить вид периодического сигнала, имеющего заданную полосу частот (от ω_н до ω_в ), согласованная фильтрация которого максимизирует энергию выходного сигнала. Другими словами, требуется найти такой сигнал x ₁ ( t ) , который обеспечивает выполнение условия

T j [x(t)]2 d t ^ max , 0                          x1

t где x(t) = jх1(т - ф)x2 (t - т)dт .

Например, зондирующий сигнал x ₁ ( t ) может иметь вид:

x 1 (т ) = sin( roт ), x₁(т ) = sin[( ® „ + кт )т ], x 1 (т ) = sin[ ® ( т ) т ].

Все эти функции должны быть определены на интервале времени [0, T x ].

Задача оптимизации может быть решена в несколько упрощенной постановке. Например, при рассмотрении простейших, линейно-частотно-модулированных (ЛЧМ) сигналов было показано, что оптимальным является значение коэффициента пропорциональности, равное нулю. Наибольшая энергия выходного сигнала для сигналов из класса ЛЧМ-сигналов достигается при нулевых (или близких к нулю) девиациях частот.

В соответствии с законом сохранения энергии верхним пределом энергии в системе рис. 3 является энергия зондирующего импульса — сигнала передатчика

t

E ( t ) = a j х" 2 (т )d т ,                    (4)

где а — коэффициент пропорциональности.

В случае постоянной частоты и при постоянном фазовом сдвиге ф сигнала передатчика x 1 ( t ) =

= A sin( rot ) энергия зондирующего импульса равна

E (t) = aA 2[ t /2 - sin(2 rot )/(4ro)] = = aA 2[ t /2 - Tsin(2rot)/(8п)], где Т — период колебаний входного сигнала, T = 2n

ω ^.

Поскольку для эффективной работы ПАВ-устройств длительность зондирующего импульса не может быть меньше 5 - 7 периодов сигнала x 1 ( t ), т. е. t >  (5 ^ 7)T , то с достаточной точностью можно считать

E ( t ) » aA ² 1 /2.                   (5)

Из формулы (5) следует, что в первом приближении энергия зависит только от амплитуды и длительности и не зависит от частоты зондирующего сигнала.

Далее рассмотрим возможности оптимизации чувствительности выходного сигнала, варьируя значения фазового сдвига. Система дифференциальных уравнений, соответствующая рис. 3:

x = У ,

У = -ro 2 x - ro₂ sin( ro 1 1 - ф ).

Система уравнений (6) позволяет моделировать скачкообразное изменение фазового сдвига ϕ на интервале интегрирования.

АППРОКСИМАЦИЯ РЕЗУЛЬТАТОВ ЧИСЛЕННОГО ЭКСПЕРИМЕНТА

На рис. 4 приведены графики нормированных к максимальной величине зависимостей амплитуды выходного сигнала x , полученных в результате численного интегрирования системы (6), и ее аппроксимации функцией

A = |(1 - z )|cos( ф /2) + z             (7)

на интервалах фе[-п, п] и фе[-3п, +3п], где z = min A « ——, 2N — число групп отражателей в ϕ 2N отражающей структуре (рис. 2).

Для определения координаты максимальной чувствительности вычислим вторую производную от функции (7), приравняем ее нулю и решим полученное уравнение относительно угла фазового сдвига:

d         d 2          d 2            ϕ

—C (Ф) = -тч A (Ф) = TT[(1 - z)cos + z] = dϕ      dϕ2      dϕ2         2

• (1 - z )     Ф _п

• =  ---- cos— = 0,

где C(ϕ) — чувствительность амплитуды A(ϕ) сигнала х к изменению фазового сдвига ϕ на смежных полупериодах, C(ф) = —A(ф). Корень dϕ этого уравнения ф = ± п.

Следовательно, наибольшего значения чувствительность достигает на концах интервала ^{[ - п} , ^{п ] :} C max ( ± ^{п )} = + 2 ^отн. еД. / раД.

Изменение фазы сигнала на π эквивалентно изменению скорости ПАВ на 0.05 % при задержке, равной 1 мкс на частоте 1 ГГц (915 МГц). Применение высокочувствительных срезов позволит в несколько раз увеличить чувствительность.