Оптимизация электрических сетей со стохастическими элементами

Уже более десяти лет во многих странах развивается концепция так называемых умных электрических сетей (Smart Grids) [1]. Данная концепция включает рассмотрение таких вопросов, как:

• •    применение силовых элементов ЭЭС, имеющих в своем составе компьютерные (цифровые) устройства управления и использующихся для производства, накопления, передачи, распределения и потребления электроэнергии;

• •    применение современных информационно-коммуникационных технологий в управлении ЭЭС;

• •    новые методы управления ЭЭС, использующие в том числе комплексные вычислительные алгоритмы и машинное обучение;

• •    применение регулирующих устройств, обеспечивающих активное поведение потребителей по управлению собственным электропотреблением;

• •    использование возобновляемой и малой распределенной генерации.

Особую актуальность данная концепция имеет в крупных городах, когда к вышеперечисленным свойствам электрических сетей добавляются электромобили. В будущем рост доли электрических автомобилей будет только увеличиваться. Так, например, во время конференции по климату в Париже в 2015 г. была принята совместная инициатива “Парижская декларация по электромобильности и изменению климата и призыв к действиям”. Для достижения целей, заданных данной декларацией электромобили должны представлять 35 % мировых продаж автомобилей к 2030 г. [2].

Для качественной оценки потенциального влияния электромобилей на электрические сети была определена доля участия электромобилей в общей нагрузке электрических сетей на основе следующих открытых статистических данных: данные о количестве автомобильного транспорта на душу населения [3]; статистические данные и прогноз населения по странам [4]; статистические данные и прогноз потребления электроэнергии по странам [5].

Также был экстраполирован рост объемов продаж электромобилей [6] с учетом текущей тенденции и декларируемой доли в 35 % от общего объема продаж автомобилей.

В результате на примере потребления электроэнергии таких стран, как Россия, США, Франция и Германия (рис. 1), доля прогноза потребления электромобилей оказывается существенной и доходит до 25 % (рис. 2). Приведенные данные не учитывают возможное насыщение рынка автомобилей, но для качественной оценки такой подход допустим.

Электромобили особенно хорошо высвечивают проблемы, которые возникают при моделировании умных электрических сетей. Поэтому опишем структуру процесса оптимизации на примере городской электрической сети с наличием зарядных станций для электромобилей и аккумулирующих устройств, работающих по технологии V2G. Когда электромобили подключаются к электрической сети несогласованно и на полную мощность, требуемую для их зарядки, то такое нескоординированное поведение приводит к возникновению местных проблем с энергосистемой, таких как дополнительные потери электроэнергии, отклонения напряжения, и тем самым к ухудшению качества электроэнергии и потенциальному снижению устойчивости ЭЭС.

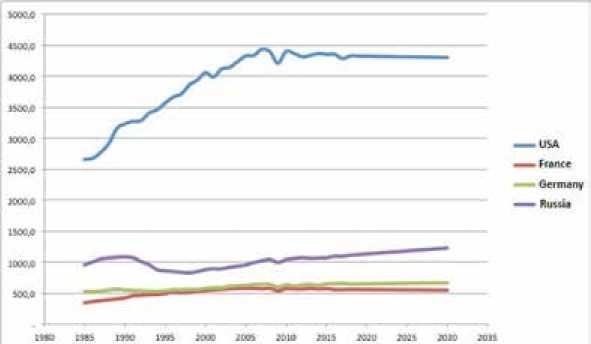
Рис. 1. Прогноз электропотребления

Fig. 1. Power consumption forecast

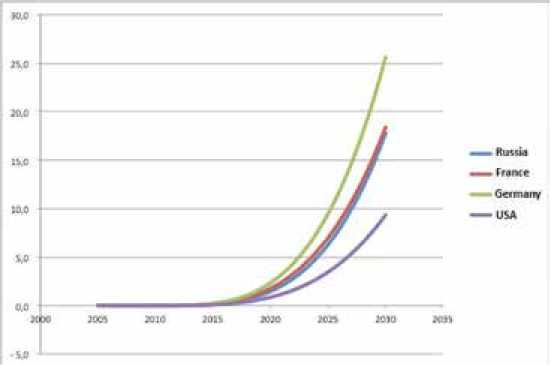
Рис. 2. Рост доли электромобилей в объеме нагрузки электрических сетей в процентах

Fig. 2. Growth in the percentage of electric vehicles load

Постановка задачи оптимизации

Целями оптимизации с точки зрения сетевой компании могут быть: минимизация потерь в сети, обеспечение требуемых уровней по напряжению, оптимизация по стоимости генерации электроэнергии. С точки зрения пользователей EV, важным вопросом является оптимизация зарядки EV по экономическим критериям: зарядка EV во время минимальных тарифов, использование собственных ресурсов генерации.

Такая комплексная постановка проблемы влечет за собой частичную противоречивость интересов участников процесса (сетевых компаний и владельцев EV). Владельцы EV желали бы иметь возможность заряжать свой электромобиль в любое удобное время и в любом удобном месте по наименьшим тарифам. Для сетевой компании же важно минимизировать свои издержки на передачу электроэнергии. При этом надежность электроснабжения важна всем участникам процесса.

Очевидно, что работа с единой моделью, представляющей городскую электрическую сеть и каждый отдельный электромобиль, не возможна из-за ее сложности. Поэтому наиболее оптимальным вариантом решения комплексной задачи оптимизации городской сети с электромобилями служит двухуровневая динамическая оптимизация. Верхний уровень представляет собой стохастическую модель городской электрической сети. Нижний уровень – это групповые контроллеры заряда EV, оптимизирующие процесс заряда на уровне локальных микрогрид или зарядных агрегаторов.

Нижний уровень оптимизации

Целевая функция оптимизации на нижнем уровне учитывает экономическую эффективность заряда и выдачи мощности в случае подключения EV по технологии V2G. Минимизируемая целевая функция оптимизации может определяться следующим образом:

КРяСО) = с_е(р«,(О) + Q(p_w(O) + c (|p_ev(t) - p_d(t)|). (1)

Первые два члена этой суммы определяют стоимость получаемой из внешней сети электроэнергии ( c e ) и стоимость электроэнегии, генерируемой внутри микросети ( c , ). Также в функции оптимизации присутствует член, определяющий отклонение мощности EV от требуемой. График изменения мощности p ev ( t ) может представлять собой как мощность нагрузки, так и мощность генерации. Требуемый график мощности EV (p d ( t )) вычисляется в результате оптимизации всей городской электрической сети и передается из системы управления верхнего уровня.

Оптимизация на нижнем уровне должна учитывать стохастический характер поведения EV Методами решения такой задачи, как правило, являются варианты динамического программирования, такие как приближенное динамическое программирование, учитывающее стохастический характер исходных данных [7, 8]. Также применяют методы адаптивного динамического программирования, использующие в качестве адаптации стратегии перехода системы от состояния к состоянию, подход обучения с подкреплением [9]. Для уменьшения размерности решаемой задачи применяют такие методы, как метод опорных векторов.

Кроме классического решения задачи оптимизации с помощью динамического программирования также могут быть применены эвристические методы машинного обучения, такие как глубокие Q-сети, генетические алгоритмы, метод роя частиц и др.

Описание модели верхнего уровня

Оптимизация на верхнем уровне представляет собой многоцелевую оптимизацию, которая может решаться различными методами, такими как: оптимум по Парето [10], минимизация расстояния до точки утопии [11], методы объединения в одноцелевую функцию. Среди объединяющих методов можно выделить следующие: метод взвешенной суммы [12, 13], лексикографический метод [14], взвешенный минимаксный метод [15], экспоненциальный взвешенный критерий [16], метод взвешенного произведения [17], целевое программирование [18], физическое программирование [19].

Наиболее простым и достаточно эффективным способом является метод оптимизации взвешенной суммы, когда отдельные целевые функции суммируются в одну с помощью соответствующих весов.

•ДХ) =^«.1.^ №)<0, .2)

где f ( x ) - целевая функция по одному из рассматриваемых критериев; w , - весовой коэффициент, соответствующий подзадаче целевой функции; x - вектор управляющих параметров; g( x ) - ограничения на сами управляющие параметры и функциональные ограничения, определяющие системные режимные ограничения. Также в эти ограничения входят ограничения на объем управления, вычисляемые на уровне агрегаторов, управляющих зарядкой EV.

Использование весов позволяет гармонизировать отдельные составляющие целевой функции, масштабируя их таким образом, чтобы это максимально удовлетворяло целям сетевой компании. Рационализировать выбор весов позволяет метод анализа иерархий [20].

Перечислим составляющие целевой функции, входящие в задачу оптимизации верхнего уровня городской электрической сети с электромобилями:

• 1.    Минимизация стоимости генерации. В данной задаче она включает не только стоимость производства энергии в городской энергосистеме, но и минимизацию затрат на закупку электроэнергии у генерирующих компаний.

• 2.    Минимизация потерь в электрической сети

• 3.    Минимизация отклонений по напряжению

• 4.    Уменьшение влияния на окружающую среду.

^(p_fl) = УдуЛс_1гРд1 + C_Up_gi + С_<0).

Управляющие параметры оптимизации: p g – генерация активной мощности внутри сети или инъекция мощности в сеть из внешней питающей сети. G – множество генераторных узлов.

Приоритет учета и масштабирование параметров целевой функции задаются константами: c i ₂ , c i 1 , c i о - константы, масштабирующие учет стоимости генерации.

^•(Ю = Z[tj)€B kPijtVi.VjY где Apij - потери в ветви i-j; Vi, V - напряжения в узлах смежных ветвей; B - множество индексов узлов для каждой ветви в схеме замещения.

^(Ю = ^|А^|,

AV i - отклонения напряжения от допустимого; N - множество узлов, где контролируется напряжение.

Функция эмиссии загрязнения может быть выражена как полиномиальная функция выходной активной мощности генератора следующим образом:

fpolCPy) = LeG^o + ецрд1 + ei2pgi + - + e,^, где ei – коэффициенты загрязнения; k – порядок.

В качестве ограничений на целевую функцию (2) выступают: ограничения на инъекцию реактивной мощности в балансирующих по Q узлах, ограничения на диапазон изменения управляющих параметров, а также ограничения в виде баланса полной мощности в сети, который, в свою очередь, вычисляется решением системы уравнений баланса мощности где AN - вектор инъекций мощности; diag(V) - диагональная матрица составляющих комплексов узловых напряжений; Y – матрица комплексов проводимостей.

Вероятностная постановка задачи

В вероятностной постановке целевая функция (2) может быть переписана как

Вместо детерминированных составляющих целевой функции f i ( x ) здесь присутствуют распределения вероятности этих функций p(f i ( x )).

Как уже было показано, значения составляющих обобщенной целевой функции вычисляют на основе вектора состояния системы, представляющего собой напряжения в каждом – 411 – узле электрической сети, а также значений мощности генерации. Распределение вероятности мощности генерации узлов, не являющихся балансирующими, может быть задано априорно в виде нормального распределения. Таким образом, вся сложность вычисления составляющих целевой функции сводится к вычислению распределения вероятности напряжений, которые, в свою очередь, могут быть получены из уравнений баланса мощности в электрической сети.

В литературе такая постановка известна как вероятностный расчет потокораспределения (Probabilistic Powerflow) и впервые предложена в [21]. Однако при этом принимают допущение о линейности системы, пренебрегают потерями в сети, а также отсутствует зависимость между активной и реактивной мощностью. Такой подход допустим только для приближенного расчета балансов мощности в электрической сети. Развитие метода вероятностного расчета потоко-распределения с тех пор продолжалось во множестве работ, таких как [22-24].

Суть вероятностного расчета потокораспределения заключается в представлении уравнения баланса электрической мощности в вероятностной постановке в линеаризованном виде:

,5, где J – матрица Якоби текущего состояния системы.

В новых работах по данному направлению [23, 24] решается проблема вычислительной сложности операции свертки, которая может быть не применима для больших систем. Данная проблема решается аппроксимацией свертки полуинвариантами характеристической функции случайной величины. Однако данные работы также основываются на допустимости о линейности решаемой задачи. Таким образом, или этот подход может применяться при планировании режимов энергосистемы, когда модель может быть упрощена до линейной, или аппроксимация должна выполняться на каждой итерации решения нелинейной системы уравнений методом Ньютона с использованием обновленных значений матрицы J.

В общем случае, распределения вероятностей инъекций мощности могут быть разными для разных узлов. Так, например, модель ветровой электростанции использует распределение Вейбулла [25] для определения вероятности скорости ветра, на основе которой рассчитывают распределение генерации ветровой электростанции. Распределение мощности солнечной электростанции рассчитывают с использованием функции бета-распределения, описывающей солнечную инсоляцию [26, 27]. Модель нагрузки обычно задают нормальным распределением со средним значением и стандартным отклонением. Что касается зарядной нагрузки EV, то она также может быть представлена нормальным распределением для каждого момента времени. При этом в течение суток ее математическое ожидание и дисперсия меняются.

Значительно проще вычислять вероятностное потокораспределение можно в случае, если все инъекции в сети представлены нормальными распределениями. Распределение вероятности целевой функции для каждого момента времени в этом случае будет также представлять собой нормальное распределение. Здесь видится обоснованным применение методов интервального анализа [28] для оценки распределения вероятности вектора состояний системы p ( V) и, как следствие, распределения вероятности целевой функции.

При использовании интервальной арифметики нормальное распределение вероятности инъекций мощности представляют в виде интервала

• s,    = [Sot - ®si. Koi + o^]-

• Систему уравнений баланса электрической мощности при этом записывают в виде интервальной системы уравнений:

s = V - У • 1/, где s – брус инъекций мощности; v – искомый брус переменных состояния системы.

Решение данной задачи может быть выполнено с помощью внешнего оценивания множеств решений интервальным методом Ньютона [29]. По интервальным значениям переменных состояния системы аппроксимируется математическое ожидание и дисперсии переменных состояний системы.

Динамическая оптимизация режима

В качестве исходных данных для оптимизации режима имеется прогноз изменения параметров режима на заданное время. Прогнозный горизонт разбит на отдельные временные срезы через равные промежутки. Каждый срез представляет собой минимально необходимый набор исходных данных для расчета установившегося режима. Остальные параметры схемы замещения заданы для всех режимов и не меняются с течением времени.

Задачей динамической оптимизации является минимизация суммарной ЦФ на всем прогнозном временном горизонте за счет выбора состава и времени управляющего воздействия:

rnin ХГ c/t^?)-                                                       (61

В отличие от статической оптимизации одного режима в задаче динамической оптимизации важно учитывать «стоимость» управляющих воздействий, которая зависит не только от вектора состояния системы, но и от времени.

Стоимость управления тем или иным оборудованием зависит от таких факторов, как: остаточный ресурс оборудования; приоритет использования УВ; минимально допустимое время между коммутациями одним и тем же устройством.

Задача оптимизации (7) с учетом стоимости воздействия записывается как

min £Г=1А№.0 = zr=i(fdt№) + Zf=1A,(xtj,t)), где Xt – управляющие воздействия доступные в момент времени t; fdt – функция статической оптимизации каждого режима для времени t; fci – монотонно убывающая функция стоимости управляющего воздействия xti, зависящая от времени воздействий, которые были выполнены до времени t. Примерный вид штрафной функции представлен выражением (7). Смысл данного выражения такой, что после применения управляющего воздействия повторное его применение в течение некоторого времени должно быть заблокировано высоким значением штрафной функции (рис. 3). Через некоторое время стоимость воздействия снижается до постоянной величины ci.

fa - k_Ci(th(t_p. -1 + M_b) + 1) + c_t,                                (7)

где t_p - время предыдущего применения данного управляющего воздействия; k_c , >  0, c i > 0, Δ t b > 0 – некие масштабирующие и сдвигающие константы.

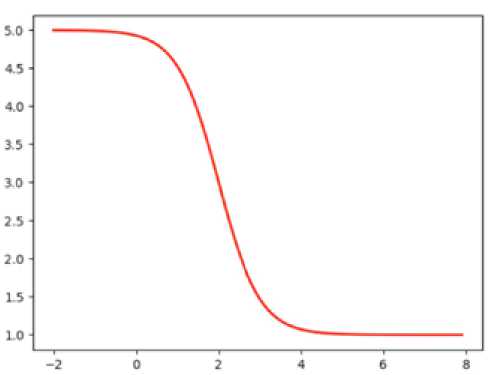
Рис. 3. Пример функции стоимости управляющего воздействия

Fig. 3. Example of the control action cost function

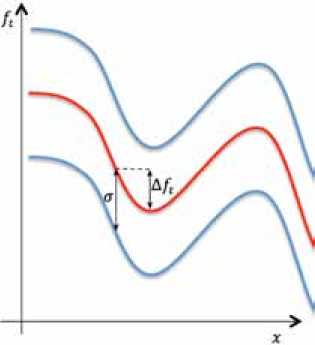
Рис. 4. Влияние дисперсии целевой функции на процесс оптимизации

Fig. 4. The impact of the variance of the objective function on the optimization process

Наличие в целевой функции зависимости от времени применения предыдущих управляющих воздействий делает процесс оптимизации не марковским процессом. Так как «стоимости» воздействий и зависимости «стоимости» от времени для разных устройств различны (например, РПН трансформаторов переключать можно редко, а управлять с помощью УШР можно достаточно часто), то отстроиться от таких воздействий и вернуть процессу оптимизации марковские свойства не получится.

Дополнительную сложность вносит необходимость учета стохастичности исходных данных. Величина дисперсии целевой функции σ может быть больше, чем улучшение величины целевой функции в процессе оптимизации Δ f t (рис. 4). В предельном случае, если величина неопределенности целевой функции такая, что она может практически равновероятно принимать любое значение из допустимого диапазона, оптимизировать такой режим смысла не имеет.

При решении динамической оптимизации в детерминированной постановке предлагается применять адаптивный вариант сверхбыстрого отжига. В отличие от детерминированной постановки при проверке необходимости фиксации текущего состояния как глобального оптимума значение «энергии системы» учитывается с допуском, определяемым дисперсией.

Пример динамической оптимизации электрического режима

В качестве примера для динамической оптимизации была выбрана модель реальной энергосистемы (рис. 5), подготовленная в комплексе АНАРЭС [30]. Количество узлов в модели узлы/ветви для данной электрической сети 1248 и количество ветвей 1481. Количество элементов в сети значительно больше, так как модель узлы/ветви формируется топологическим процессором, эквивалентирующим однолинейную схему электрической сети.

Для данной энергосистемы имелись архивные данные, представленные в виде набора рассчитанных электрических режимов с периодичностью в 30 мин. Глубина архива 1 месяц. При промышленном применении данного алгоритма оптимизация будет проводиться на основе прогноза изменения параметров режима на определенный горизонт времени. Однако для проверки самого алгоритма оптимизации архивных данных достаточно.

На результатах расчета серии статических оптимизаций режима можно видеть, что возникает необходимость достаточно частого изменения управляющих воздействий. На рис. 6 это показано на примере одного из изменяющихся управляющих воздействий (коэффициента трансформации). По оси абсцисс отложено время.

В результате динамической оптимизации изменение параметров становится более редким (рис. 7).

Сходимость процесса динамической оптимизации методом адаптивного сверхбыстрого отжига представлена на рис. 8. fc0 на графике показывает значение целевой функции на всем рассматриваемом временном диапазоне без учета составляющей стоимости воздействия, зависящей от времени. Видно, что суммарное значение целевой функции после динамической оптимизации превышает значение fc0, так как отдельные режимы на рассматриваемом временном диапазоне могут отойти от оптимального значения. Полное время выполнения динамической оптимизации для прогнозного диапазона в 1 месяц составило 25 мин.

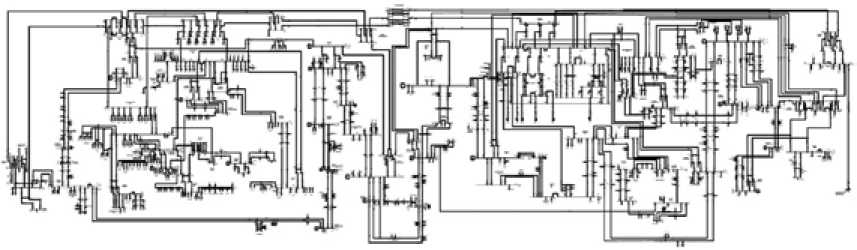
Рис. 5. Схема энергосистемы Иркутской области

Fig. 5. Electric grid of the Irkutsk region

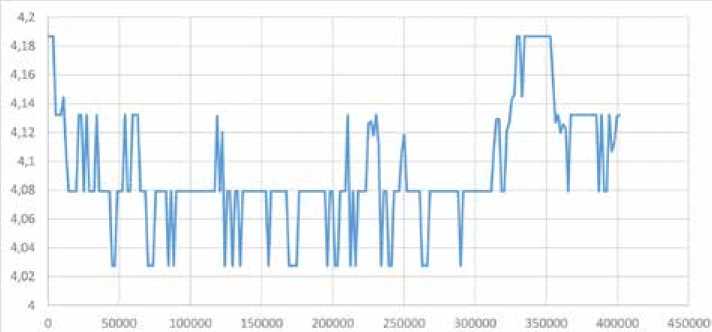
Рис. 6. Изменение одного из управляющих воздействий в серии статических оптимизаций

Fig. 6. Changing one of the control actions in a series of static optimizations

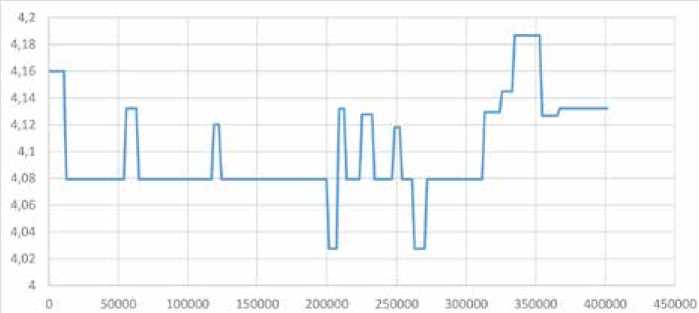
Рис. 7. Изменение одного из управляющих воздействий после динамической оптимизации

Fig. 7. Change in one of the control actions after dynamic optimization

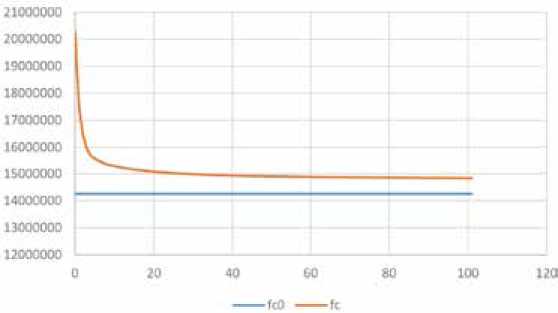
Рис. 8. Процесс сходимости динамической оптимизации

Fig. 8. Dynamic optimization convergence process

Заключение

Предлагаемая методика моделирования и оптимизации распределительных сетей со стохастическими элементами реализована в виде встраиваемого программного обеспечения и может использоваться в системах автоматического оптимального и противоаварийного управления.

Для операционных систем семейства Windows встраиваемая версия реализована в виде COM-сервера. Для Linux возможна реализация встраиваемой версии подсистемы оптимального управления в виде RESTful web-сервера, взаимодействующего с целевой системой в формате JSON.

Подсистема для оптимального управления напряжением и реактивной мощностью ЭЭС разработана на основе программного обеспечения АНАРЭС [30]. Кроме систем автоматического управления предлагаемый инструмент моделирования режимов может использоваться как самостоятельный продукт или встраиваться в SCADA-системы. Встраиваемая версия комплекса АНАРЭС предназначена для использования расчетных функций АНАРЭС во внешней SCADA-системе. Встраиваемая версия АНАРЭС содержит все расчетные модули, имеющиеся в полной интерактивной версии АНАРЭС. Кроме того, встраиваемая версия содержит специальную версию топологического процессора, позволяющего работать с топологией электрической сети, передаваемой из внешней SCADA-системы.

Функции, реализуемые встраиваемым инструментом моделирования режимов:

• •    Оценивание состояния и достоверизация электрических режимов.

• •    Прогнозирование электрических режимов.

• •    Статическая и динамическая многокритериальная оптимизация.

• •    Расчет и анализ установившихся режимов.

• •    Расчет токов коротких замыканий.

• •    Моделирование электромеханических переходных процессов.

• •    Анализ статической и динамической устойчивости.

Благодарность / Acknowledgement

Работа выполнена в рамках программы фундаментальных исследований СО РАН, рег. № АААА-А17-117030310438-1, научный проект III.17.4.2.

This work was supported in part by the program of fundamental research of the Siberian Branch of the Russian Academy of Sciences and carried out within the framework of the research project III.17.4.2, No. AAAA-A17-117030310438-1.