Оптимизация энергетических потоков в автономной системе электроснабжения с использованием нетрадиционных источников энергии

Рассматривается автономная система электроснабжения небольшого поселка, включающая несколько возобновляемых источников энергии: ветроэнергетическая установка, солнечная батарея и дизель-генератор в качестве резервного источника электроэнергии. Не исключается также подключение потребителей к централизованной сети. Потребителями являются жилые дома загородного типа, магазин, школа, почта, исследовательская лаборатория, яхт-клуб. Потребители имеют возможность получать электроэнергию от собственных источников или по линии электропередачи 380 В от подстанции ТП яхт-клуба мощностью 320 кВА. Для обеспечения потребителей теплом и горячей водой служит котельная, работающая на природном газе. Газ поступает от газораспределительной станции, расположенной в 1,5 км от потребителей. Суммарное годовое электропотребление составляет 243 800 кВт·ч.

На основании общей характеристики и анализа энергопотребления можно сделать вывод, что основная доля в энергопотреблении поселка (60 %) приходится на тепловую энергию. Она же составляет наибольшую долю в стоимости годового потребления энергоносителей.

Моделирования и решения экономикоматематических задач

Задача состоит в определении такого уровня использования энергоресурсов, при котором суммарные энергозатраты достигают минимального значения. Кроме того, необходимо обосновать параметры автономного энергокомплекса и оптимизировать структуру энергетических потоков. Такие задачи решаются с использованием методов математического моделирования, являющихся наибо- лее достоверными и обоснованными. Адекватность принятой модели и действительности возможна при достаточно глубоком изучении закономерностей развития отдельных факторов, влияющих на энергопотребление.

Для моделирования и решения экономикоматематических задач необходимо иметь информацию об энергоресурсах и их наличии, процессах производства, распределения и потребления энергии, а также нормативы и санитарно-гигиенические требования [1].

При исследовании вопросов, связанных с оптимизацией структуры энергетических потоков, используется системный подход при выборе решений, в котором объект рассматривается как сложная система, состоящая из множества элементов, и работа каждого элемента оптимизируется с учетом его связи с другими элементами и влияния на работу объекта в целом. Решение задачи оптимизации осуществляется с помощью аналитических и численных методов. Математическая модель представляет собой систему уравнений и неравенств, отражающих взаимосвязи различных факторов в отдельных элементах объекта и между элементами. Модель должна отвечать требованиям содержательности с одной стороны, и простоты описания с другой.

При оптимизации структуры энергетических потоков автономного энергокомплекса одной из основных задач является определение такого уровня использования энергоресурсов, при котором доминирующий экономический критерий – удельные энергозатраты – достигает минимума. При этом учитываются необходимые в каждом конкретном случае ограничения и соблюдаются все условия сопоставимости при сравнении раз- личных вариантов энергоснабжения и энергоиспользования [2].

Использование нетрадиционных возобновляемых источников энергии может рассматриваться как самостоятельная часть общей системы электроснабжения. При этом следует учитывать, что солнечная энергия (при существующих условиях и техническом решении) может производить электрическую и тепловую энергию, ветровая энергия – электрическую и механическую (например, водоподъем). Системы с использованием нетрадиционных возобновляемых источников энергии исключают элементы, связанные с добычей, транспортировкой и переработкой органического топлива и отсутствием выбросов в атмосферу. Кроме того, снижается радиус транспортировки энергии за счет отсутствия питающих сетей.

К недостаткам относится циклический характер поступления энергии от ВЭУ и СЭС в течение года, сезона и суток. Следовательно, использование этих источников энергии будут накладывать определенные ограничения, связанные с неравномерностью подачи энергии во времени. В связи с этим необходимо решать задачу о рациональном соотношении между различными источниками энергии при электроснабжении потребителей.

Математическая модель оптимизационной задачи

Энергетические потоки представляют собой передаваемую энергию в течение какого-либо промежутка времени. В основном это потоки электрической и тепловой энергии, которые могут быть получены от различных источников (рис. 1).

Потребители используют только электрическую энергию для целей освещения, привода механизмов, работы электробытовых приборов. Для отопления и горячего водоснабжения может быть использована электрическая, тепловая энергия или газ. Для работы газовых плит – только газ. Структурная схема энергетических потоков исследуемого объекта показана на рис. 2. На рисунке стрелками показаны направления энергопотоков, количество потребляемой энергии – Хi. Цифрами на рисунке обозначены источники энергии (1–6) и потребители энергии (7–14). Котельная рассматривается одновременно как потребитель и источник энергии.

Математическая модель оптимизационной задачи представлена в виде целевой функции, минимум которой необходимо найти mnp

^ j = 1 ^ i = 1 ^ q = 1 i , j , q ^a i , q x i , j , q +

+У "Mp A',-^ Ek ,3/C ^ min (1) ^ j =1 Z—ii =1 Z—iq=1 1, j,q 1=11=1 l l при ограничениях:

У ™УР ,a, „■ Xj = =Xy ay± ± C;(2)

j=1 Z-^q=1 i,q i,.j,q        iq-'i       i’

У”,yp ,a, X,, =±C,;

z—ii =1 z—iq=1 i,q i,.j,q         j’ ai, j,q xi, j,q i, j,q ;

4^ C -^ 4;

A j^ C j ^ B j ;

i = 1,2, _ , n ;

j = 1,2, _ , m ;

q = 1,2,_, p, где Зi, j,q – энергетические затраты j-го потребителя при использовании энергии вида q, поступающей от i-го источника, руб; ai q - удельный расход топлива на выработку энергии типа qi-м источником, т. у. т. на единицу энергии; xi, j,q – количество передаваемой энергии вида q от i-го источника к j-му потребителю, единиц энергии в

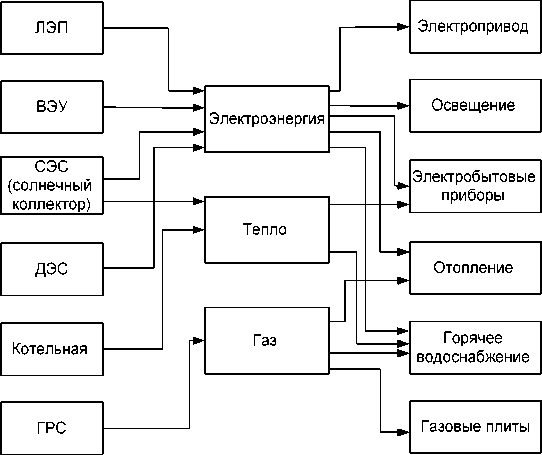
Рис. 1. Потоки энергии от различных источников

Четошникова Л.М., Морозова Е.А

Оптимизация энергетических потоков в автономной системе электроснабжения…

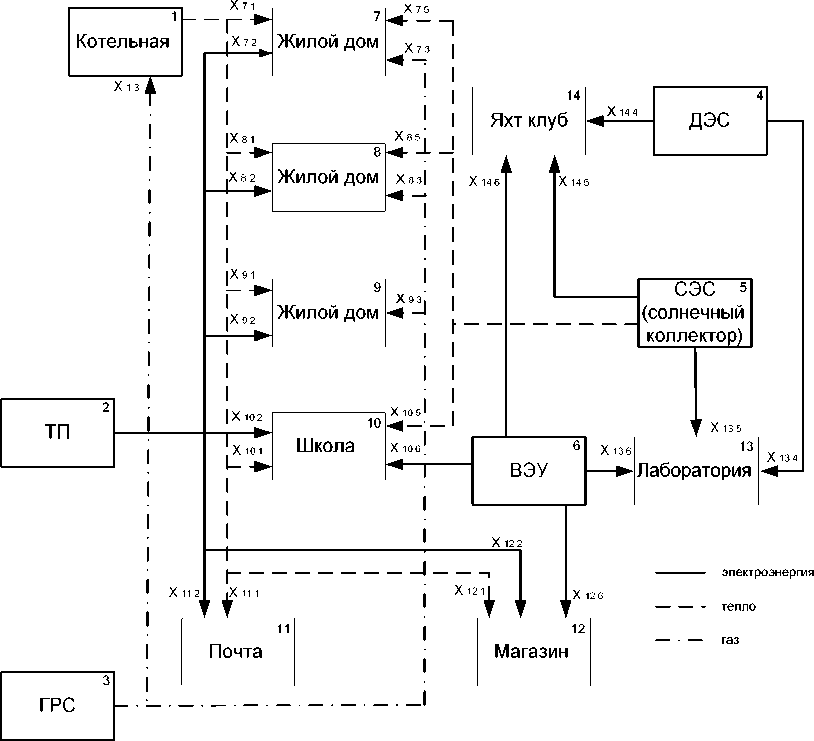
Рис. 2. Структурная схема энергетических потоков

год; З', j,q - составляющая приведенных затрат, отражающая капиталовложения и эксплуатационные издержки без учета энергетической составляющей, руб./год; Зl – затраты на энергию, по- ступающую дополнительно в систему или уходящую из системы по связи l, руб./т. у. т.; Xiq - удельный расход энергии на производство 1 кВт-ч энергии, вырабатываемой i-м источником; yi – количество произведенной продукции i-м источником, единиц энергии в год; ai, j,q , bi, j,q – предельные значения величины xi j q ; A (Aj),

B i ( B j ) - предельные значения величины C i ( C j ) ; p – число видов энергоносителей [3].

Уравнения (2) и (3) записываются отдельно для источников и потребителей энергии. Ограничения представляют собой верхний ( a ) и нижний ( b ) пределы использования ресурсов. Переменными в модели являются связи х , выражающие годовое потребление энергоресурсов потребителями.

Используя только первую составляющую целевой функции, можно определить энергозатраты в год без учета затрат на капиталовложения и эксплуатационные издержки, для учета которых не- обходимо использовать вторую составляющую целевой функции. Если энергия поступает в рассматриваемую систему извне или передается из системы на сторону, расчет следует производить по трем составляющим.

Переменные х_i в уравнении целевой функции представляют собой количественное выражение того или иного энергетического потока. Их значения не постоянны и изменяются в определенных пределах. Нижний предел определяется минимальным количеством энергии, исходя из норм потребления и требований энергосбережения. Верхние пределы изменения величины х i соответствуют существующему энергопотреблению, включая все виды потерь [3].

Ограничительные уравнения источников и потребителей энергии записываются согласно рис. 2.

Уравнения для источников энергии:

И¹: ^ ( x 7! + x gi + x 9! + x ioi + x _m + ^х _ш ) < ^X j y j ; (4) И² : « 2 ( ^x 72 + ^x 82 + ^x 92 + ^x 102 + ^x 112 + ^x 122 ) < ^X 2 У 2 ; ⁽⁵⁾ И3: a 3 ( X 13 + X 73 + X 83 + x 93 ) < X , y 3 ; (6) ^И4: « 2 ( ^x 144 ^{+ x} 134 ) <^X 4 У 4 ; ⁽⁷⁾ И5 : « 1 ( ^x 75 + ^x 85 + x !05 ) + « 2 ( x !45 + ^x _B5 ) < X ₅ y 5 ; ⁽⁸⁾ И6 : « 2 ( x io6 + ^x i2₆ + ^x i3₆ + ^x i4₆ ) < ^X ₆ У ₆ . (9)

Уравнения для потребителей энергии:
П7 : α 1 x 71 +α 1 x 75 + α 2 x 72 + α 3 x 73 ≤ β 7 z 7 ;	(10)
П8 : α 1 x 81 + α 1 x 85 + α 2 x 82 + α 3 x 83 ≤ β 8 z 8 ;	(11)
П9: α 1 x 91 + α 2 x 92 + α 3 x 93 ≤ β 9 z 9 ;	(12)
П10: α 1 x 101 + α 1 x 105 + α 2 x 102 + α 2 x 106 ≤ β 10 z 10 ;	(13)
П11: α 1 x 111 + α 2 x 112 £ β 11 z 11 ;	(14)
П12: α 1 x 121 + α 2 x 122 + α 2 x 126 ≤β 12 z 12 ;	(15)
П13 : α 2 x 134 + α 2 x 135 + α 2 x 136 ≤ β 13 z 13 ;	(16)
П14: α 2 x 144 + α 2 x 145 + α 2 x 146 ≤β 14 z 14 ;	(17)
П1: α 3 x 13 ≤ β 1 z 1 .	(18)

Заключение

В результате решения оптимизационной задачи определяются оптимальные энергопотоки и удельные годовые приведенные затраты. Задача решается методом «ветвей и границ» дискретного программирования.