Оптимизация кабельной сети сбора мощности морских ветроэлектростанций с применением параметризованного эвристического алгоритма

Ввиду стремительного развития морской ветроэнергетики актуальной задачей является совершенствование методик выбора оптимальных проектных решений для морских ветроэлектростанций (МВЭС) с целью повышения их эффективности и надежности. Одной из важных задач проектирования МВЭС является построение экономичной схемы прокладки межтурбинных подводных кабелей, обеспечивающих передачу генерируемой мощности от ветроустановок (ВЭУ) к сборным шинам морской трансформаторной подстанции (МТП).

Капитальные затраты, приходящиеся на компоненты электрической системы, в число которых входят силовые трансформаторы, кабели сбора и передачи мощности, распределительные устройства и прочее электрооборудование, составляют порядка 20 % от общей стоимости МВЭС [1]. Стоимость системы сбора мощности зависит от ряда ее конструктивных факторов, к которым относится: тип конфигурации сети (замкнутая/разомкнутая, неразветвленная/разветвленная), используемые сечения кабелей, а также коммутационного оборудования и аппаратов защиты [2].

Цель оптимизации состоит не только в поиске наиболее дешевого, но также технически выполнимого и надежного варианта, что предполагает выполнение следующих требований:

• -    каждый участок сети должен быть выполнен кабелем достаточного сечения, выбираемого по номинальной мощности ВЭУ для предотвращения его возможной перегрузки;

• -    схемы с пересекающимися путями прокладки кабельных линий считаются нежелательными для реализации, поскольку такая конфигурация является более дорогостоящей, создает трудности при проведении ремонта и, кроме этого, повышается риск термического износа изоляции кабелей в точке соприкосновения [3–5].

Проблема построения оптимальной схемы прокладки кабелей с учетом технических ограничений может быть сведена к задачам оптимизации на графах – поиска минимального остовного дерева с ограничением на проводимость связей (CMST) [6] или задачи маршрутизации транспорта с открытыми маршрутами (OVRP) [7]. Данные задачи относятся к классу NP-трудных, для которых алгоритмы полного перебора малоэффективны, и на практике используются методы математического программирования, эвристические и метаэвристические алгоритмы [8]. Метаэвристиче-ские алгоритмы могут найти более точное решение по сравнению с эвристическими («жадными») алгоритмами, но последние в свою очередь имеют более высокое быстродействие, что позволяет сократить время выполнения. Фактор быстродействия алгоритма особенно важен при комплексной оптимизации, предполагающей совместно с построением схемы кабельных соединений осуществление поиска оптимального расположения ветро-установок на участке предполагаемого строительства МВЭС [9].

Математическая постановка задачи целочисленного программирования для оптимизации систем сбора мощности различных конфигураций сформулирована в работе [3]. В исследовании [10] авторы используют симплекс-метод (CPLEX) для построения оптимальных схем прокладки кабельных линий с неразветвленной и разветвленной топологией. На основе OVRP реализована эвристика Planar Open Savings (POS) [5], являющаяся модификацией алгоритма маршрутизации транспорта Clarke-Wright с незамкнутыми маршрутами. Полученные результаты сравнения решений с результатом оптимизации симплекс-методом (CPLEX) показали незначительную погрешность при существенно меньших временных затратах. Однако предложенная методика ограничена возможностью построения схем с радиальной (неразветв-ленной) топологией с использованием кабеля одного сечения.

Синтез схем с разветвленной топологией может быть выполнен посредством алгоритма аппроксимации CMST-задачи – Esau-Williams (EW) [11, 12]. Проведенные исследования показывают, что подобный алгоритм позволяет получить достаточно точное решение задачи по сравнению с другими эвристическими алгоритмами [13]. Однако, как и в случае с POS, целевой функцией алгоритма является минимизация общей протяженности сети, что не позволяет осуществить построение кабельной системы, выполненной с использованием кабелей различного сечения при учете их стоимости.

В монографии [14] описан алгоритм Multispeed Local Access Algorithm (MSLA), предназначенный для выполнения синтеза структуры локальной сети с выбором требуемой скорости связи с учетом различия по их стоимости. Данный алгоритм может быть легко адаптирован к решению задачи синтеза кабельной системы сбора мощности, что дает возможность включить в процесс оптимизации выбор типа (сечения) кабеля на основе данных о его удельной стоимости.

Важным фактором, требующим учета при построении разветвленных схем, является зависимость стоимости сети от количества ответвлений, что обусловлено необходимостью установки дополнительных аппаратов защиты в узлах разветвления кабельных линий, поскольку стандартная комплектация электрооборудования не предполагает присоединение более одного входящего кабеля к распределительному устройству ветроуста-новки [5]. C учетом данного фактора задача может быть сведена к поиску минимального остовного дерева с ограничением на проводимость связей и степень узлов с учетом стоимости, зависящей от степени узла (Degree-constrained capacitated minimum spanning tree – DCMST), математическая формулировка которого дана в работе [15].

Общим недостатком эвристических алгоритмов, основанных на использовании «жадной» стратегии поиска, является проблема снижения качества решений на заключительных этапах построения остовного дерева. В работах [16, 17] исследована возможность повышения качества решений путем включения дополнительных регулируемых параметров в функцию расчета компромиссных решений, что позволяет существенно улучшить результат без значительного увеличения вычислительной сложности. На основе данного подхода предложена стратегия метаоптимизации параметризированного эвристического алгоритма EW с использованием эволюционного (генетического) алгоритма [18].

Целью данного исследования являлась разработка методики, позволяющей обеспечить построение оптимальной схемы прокладки кабельных линий системы сбора мощности МВЭС с не-разветвленной и разветвленной топологической структурой при учете различных по стоимости типов кабелей (сечений) и затрат на коммутационную аппаратуру.

Постановка задачи и алгоритм оптимизации

Топологическая структура МВЭС может быть представлена в виде ациклического связного графа G = ( V T и V S , A ) , состоящего из подмножества узлов V_T , представляющего совокупность генерирующих узлов – ветроустановок, подмножества V_S приемных узлов – подстанций, и множества A связей между парами узлов – кабельных линий. Каждой вершине графа сопоставлена точка с координатами геометрического месторасположения энергетического оборудования. Для генерирующих узлов h е V T заданы неотрицательные величины номинальной мощности генерируемой вет-роустановками P h >  0 . Параметры кабелей заданы множеством T , где кабель каждого типа t е T характеризуется его номинальной мощностью r_t >  0 и удельной стоимостью единицы длины u t >  0.

Стоимость ветви графа сети пропорциональна расстоянию между точками расположения узлов и зависит от стоимости единицы длины кабеля соответствующего типа (сечения):

c i , j = u t • l ( i , j ) ,⁽ i , ^j ) ^е A , t ^е T , (1) где c_i ^t _{, j} – стоимость связи между узлами графа, характеризующая стоимость участка линии, соединяющей ветроустановки ( i , j ), выполненной кабелем с сечением t ; l _{( i , j )} – расстояние между точками мест расположения оборудования на плане.

Стоимость дополнительного коммутационного оборудования ВЭУ, необходимого для подключения двух и более входящих кабелей от других

ВЭУ, может быть представлена нелинейной зави- симостью ωd от степени узла d [15]:

1 0, если d = 1

го j = d   [F(d), если 2 < d < dmax

,

где F ( d ) – функция расчета стоимости, зависящая от степени узла сети d ; d _max – верхняя граница допустимой степени узлов сети.

Искомым решением является основное дерево связей А минимальной стоимости, построенное с учетом ограничений на проводимость кабелей, а также с учетом стоимости сети, зависящей от степеней узлов.

Целевая функция оптимизации имеет следующий вид:

cost(G) ^

^ min

у E x t, ■ c t, + E го E^ d i , j    i , j                        d v

( i , j ) e At e T                d e {1.. d max }      v'I T

где x t e { 0,1 } - переменная, которая принимает значение x j = 1, если ветвь ( i , j ) e A включена в остовное дерево сети и x j = 0 в противном случае; z v e {0,1} - дополнительная переменная, указывающая степень узла v e V_T , которая принимает значение z d = 1, если узел v имеет степень d > 0.

Более детальное описание постановки задачи и системы ограничений приведено в работах [3, 4].

В данном исследовании для решения используется алгоритм синтеза топологии многоскоростной сети локального доступа (Multispeed local access algorithm – MSLA) [14]. Принцип работы алгоритма заключается в последовательном улучшении первоначальной структуры сети (топология «звезда») путем объединения двух нецентральных узлов в связный компонент, если стоимость такого соединения меньше стоимости их раздельного подключения к центральному узлу, если добавление такой связи не нарушает условия проводимости и не создает цикличных маршрутов.

Последовательность включения ветвей в состав остовного дерева сети определяется матрицей значений функции компромиссных решений, которая имеет следующий вид:

sv j = g^{j -} ( ^{c J +} ( g к J ) ^- g ) ) ,               ⁽⁴⁾

tt где gj = c(j 5) - стоимость связи между узлом j k компонента Cj и центральным узлом s; cij – стоимость связи между узлами i и j, принадлежащими несвязным компонентам Ci и Cj ; g(ti, j) – стоимость связи необходимой проводимости для соединения объединенного компонента ( Ci , C j ) с центральным узлом кратчайшей связью; gi = cji s) -стоимость соединения компонента Ci , содержащего узел i, с центральным узлом.

Исходный вариант алгоритма (MSLA) в процессе построения оценивает компромиссные варианты возможных соединений исходя из стоимости, зависящей от протяженности связей между узлами и типа связи (проводимости), однако не учитывает стоимости зависящей от числа подключений к какому-либо узлу (стоимости степеней узлов графа сети).

Для учета данного фактора разработана модификация алгоритма (далее по тексту Degree-constrained MSLA – DC-MSLA ), в функцию компромиссных решений которого вводится дополнительная составляющая, выполняющая оценку экономии при изменении степени узлов графа в процессе построения остовного дерева. Формула расчета матрицы компромиссных решений модифицированного алгоритма (DC-MSLA) имеет следующий вид:

sv J = g j — ( c j ^{+ ( g} ( i , J ) — g i ) ) ^{+ (} w -® deg(i + J ) ) , ⁽⁵⁾ где w – стоимость подключения к центральному узлу (подключения к шинам подстанции); m _deg ( i ₊ j ) -стоимость степени узла, рассчитываемая по формуле (2).

Блок-схема, отражающая логическую последовательность операций, выполняемых в процессе построения, изображена на рис. 1.

Шаг 1. Инициализация: выполняется построение первоначальной структуры сети, где каждый нецентральный узел соединен с центральным узлом отдельной связью наименьшей допустимой проводимости, т. е. каждая ВЭУ присоединяется к ближайшей подстанции радиальной линией с кабелем минимально допустимого сечения.

Шаг 2. Выполняется расчет матрицы компромиссных решений (5) и составляется список приоритетных соединений. Составление списка выполняется путем поиска в каждом столбце матрицы (SV) ячейки с максимальным значением, при этом индексы строк матрицы соответствуют выходным узлам, а индексы столбцов с максимальными значениями из каждой строки – входным узлам. Полученный список сортируется в порядке убывания значений, после чего для первой пары узлов проверяется возможность добавления связи посредством проверки ограничений.

Шаг 3. Проверка возможности соединения приоритетных на данной итерации узлов связью ( i , j ), которая может быть добавлена в остовное дерево при выполнении следующих условий:

Ограничение 1 . Узлы ( i , j ) принадлежат разным поддеревьям (компонентам) графа – С ( i ) и С ( j ), и их соединение не образует циклического маршрута.

Завершение

Рис. 1. Блок-схема выполнения алгоритма DC-MSLA

Ограничение 2 . Расчетный поток электрической мощности в ветви ( i , j ) не превышает допустимой мощности кабеля максимального сечения. Проверка ограничения проводимости при добавлении связи выполняется на основе расчета потока электрической мощности на участке сети:

[1 У I > г i max f (C) = ^         - C         ,                 (6)

|0 otherwise где f (C) – функция проверки условия проводимости; Ii – номинальный ток в i-м генерирующем узле участка сети (ток, вырабатываемый ВЭУ при номинальной мощности), А; rmax – допустимый ток кабеля максимального сечения из заданного списка кабелей T.

Ограничение 3 . Добавление связи ( i , j ) не приводит к превышению допустимого значения d _max, определяющего максимальную степень узла, которая ограничивает количество входящих ветвей в узел.

Ограничение 4. Рассматриваемая связь ( i , j ) при добавлении в остовное дерево не пересекает уже добавленные связи, т. е. не образует отрезка линии пересекающего другие линии связи между узлами при отображении графа сети на координатной плоскости. Для предотвращения добавления пересекающихся связей используется метод идентификации точек пересечения сегментов линий [19], выполняемый на каждой итерации алгоритма синтеза схемы.

Шаг 4. Если все условия выполняются, то два компонента объединяются путем добавления связи, соединяющей узлы i и j . Более протяженная ветвь, соединяющая объединенный компонент графа с центральным узлом, заменяется кратчайшей связью. При нарушении какого-либо условия на текущей итерации связь ( i , j ) отклоняется и исключается из дальнейшего рассмотрения.

Шаг 5. В соответствии с внесенными изменениями выполняется пересчет матрицы (SV) и возврат к шагу 2. Алгоритм выполняется до тех пор, пока в списке подключений остаются неотрицательные или ненулевые значения.

Для повышения качества решений используется стратегия, основанная на введении дополнительных параметров функции компромиссных решений (5), изменение которых позволяет варьировать дистанции (стоимости) между узлами и тем самым влиять на порядок добавления связей при построении остовного дерева. В таком случае функция расчета имеет следующий вид:

sv4= gj-(a-cj+(g(j -gi)) +

⁺ | g t ^- g t j'P^- ( w ^- ® deg( i + j ) ) ' ^Y , ⁽⁷⁾ где α – параметр масштабирования дистанций между узлами сети; β – параметр асимметрии расстояний между нецентральными узлами и центральным узлом сети; γ – весовой коэффициент стоимости степени узла.

В качестве дополнительного регулируемого параметра используется показатель степени p в

PSO

Начало

Подбор параметров эвристического алгоритма

Координаты мест расположения ВЭУ и МТП

DC-MSLA

^ X = [ а, р, у, р ]

Построение топологии кабельной системы МВЭС

G = (V,A)

Расчет целевой функции

Предельное число итераций

Проверка условия завершения

Рис. 2. Блок-схема гибридного алгоритма DC-MSLA+PSO формуле расстояния Минковского [20], посредством которой рассчитывается дистанции между узлами:

l ij = P x i j +| y i - y j\^P , ⁽⁸⁾

где x , y – координаты точек геометрического расположения узлов; р – параметр, определяющий метрику расстояния (при p = 1 расстояние городских кварталов, p = 2 евклидово расстояние, p > 2 расстояние Чебышева).

Стандартными параметрами алгоритма является вектор со значениями X = [ а = 1, Р = 0, у = 1, р = 2 ] . Для получения более точного решения в каждом отдельном случае необходимо осуществить корректный подбор значений параметров. В данном исследовании для этого используется метод оптимизации роем частиц (Particle swarm optimization – PSO). Блок-схема гибридного способа выполнения оптимизации показана на рис. 2.

Оценка эффективности методики

Проверка эффективности предлагаемой методики выполнена на основе сравнения с другими алгоритмами оптимизации, в числе которых эвристический метод построения неразветвленной сети Planar Open Savings (POS) и алгоритм Esau-Williams (EW) для построения разветвленной конфигурации сети. Проверка выполняется в соответствии с методикой, представленной в работах [5, 10], которая предполагает сравнение решений, полученных при использовании эвристических алгоритмов с результатом эталонного решения, найденного при помощи алгоритма CPLEX. В приведенных источниках в качестве одного из тестовых примеров используется схема расстановки 50 турбин ветроэлектростанции Walney 1, для которой выполняется синтез кабельной системы.

Фактическая схема компоновки МВЭС [21] показана на рис. 3.

ВЭУ

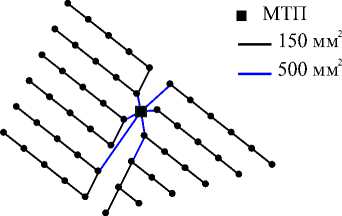
Рис. 3. Фактическая схема прокладки кабельных трасс с указанием сечений кабелей МВЭС Walney 1

Номинальная мощность каждой ВЭУ принимается равной P = 1. Проводимость кабелей С задается числом подключенных ВЭУ, суммарный ток которых не превысит допустимого тока кабеля. В качестве критерия оценки используется показатель общей длины связей L , отнесенный к эталонному решению (полученному при помощи CPLEX) [5], суммарная длина связей которого обозначена как L _opt. Расчет показателя выполняется по следующей формуле:

• 5    = L/L opt , (9)

где L – общая протяженность кабелей; L _opt – протяженность связей в оптимизированной конфигурации сети, синтез которой выполнен посредством использования алгоритма CPLEX. Результаты расчетов сведены в табл. 1.

В случае выполнения синтеза разветвленной схемы проведено 12 испытаний с различным соотношением проводимостей кабелей С 1 = 2…6 (для кабеля меньшей проводимости) и С 2 = 5…7 (для кабеля большей проводимости), при этом стои-

Таблица 1

Результаты синтеза схемы неразветвленной топологии с кабелем одного типа

Вариант	Проводимость кабеля С	Оптимальная протяженность L opt, м	Оц енка эффективнос ти δ
			POS	DC-MSLA	DC-MSLA+PSO
1	5	43 539	1,0429	1,0227	1,0177
2	6	41 587	1,0376	1,0225	1,0201
3	7	40 789	1,028	1,0352	1,0027
4	8	40 242	1,0305	1,0362	1,0076
5	9	39 752	1,042	1,0167	1,0081
6	10	39 541	1,0129	1,0139	1,0023
Максимум			1,0429	1,0362	1,0201
Среднее			1,032	1,025	1,010
Стандартное отклонение			0,0112	0,0093	0,0075

Таблица 2

Результаты синтеза схемы разветвленной топологии с кабелями двух типов

Вариант	Проводимость кабелей С		Оптимальная протяженность L opt , м	Оценка эффективности δ
				EW	DC-MSLA	DC-MSLA+PSO
	С 1	С 2
1	2	5	59028	1,1063	1,019	1,0057
2	3	5	54095	1,0421	1,0287	1,0093
3	4	5	47243	1,0949	1,0218	1,0147
4	2	6	55589	1,1367	1,063	1,0414
5	3	6	52660	1,0657	1,0414	1,0159
6	4	6	47198	1,0817	1,0231	1,0156
7	5	6	43374	1,1342	1,0302	1,0294
8	2	7	52873	1,167	1,065	1,0338
9	3	7	49354	1,1356	1,0587	1,022
10	4	7	47066	1,0614	1,0308	1,0203
11	5	7	43374	1,1069	1,0354	1,0241
12	6	7	41420	1,0979	1,0535	1,0256
Максимум				1,1025	1,0392	1,0215
Среднее				1,167	1,065	1,0414
Стандартное отклонение				0,0365	0,0167	0,0102

мость кабеля С ₂ в 1,7 раза превышает стоимость кабеля C 1 . По аналогии с предыдущим тестом для сравнения используются данные результатов оптимизации, выполненной посредством CPLEX [10]. В таком случае значение критерия сравнения эффективности рассчитывается следующим образом:

• 5    = 2 ( LL) + 1,7 • L ^))/ L opt . (10)

Результаты сравнения приведены в табл. 2.

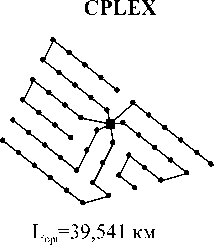
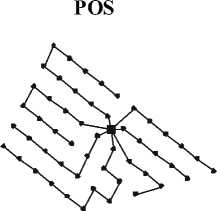
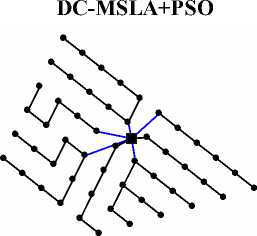
Схемы, построенные различными алгоритмами, для одного из тестовых случаев показаны на рис. 4.

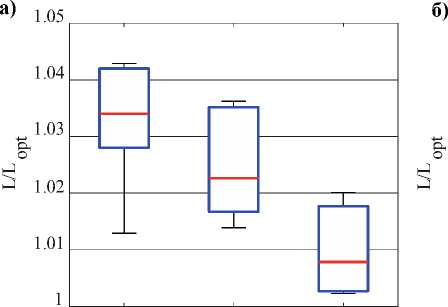
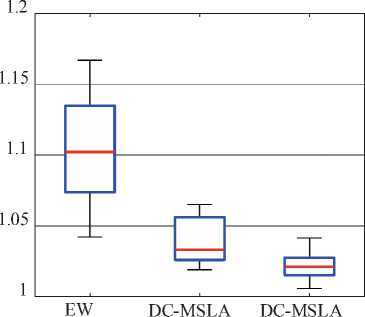
Диаграмма сравнения эффективности показателей, полученных в серии проведенных испытаний, показана на рис. 5.

Результаты испытаний показали, что решения, полученные при использовании модифицированного алгоритма (DC-MSLA) в заданных тестовых случаях, в среднем на 2 и 6 % экономичней ранее предложенных эвристических алгоритмов POS и EW. Выполнение оптимизации при помощи гибридного алгоритма DC-MSLA+PSO позволяет получить более точные решения с отклонением це- левого показателя (от результата CPLEX), не превышающим 2 и 5 %.

Чтобы продемонстрировать результат использования алгоритма при выполнении реальной проектной задачи, схема МВЭС была оптимизирована при использовании реалистичных стоимостных показателей компонентов. Капитальные затраты рассчитываются с использованием аппроксимированных зависимостей стоимости компонентов ВЭС от характеристик по методике [22].

Суммарные затраты на кабели и коммутационную аппаратуру системы сбора мощности рассчитываются по формуле

C „ ccm

2   c k • i ti , j )

( i , j , t ) e A

⁺ c k • n k ⁺ c k . d • n k . d , ⁽¹¹⁾

где c^t_kl – удельная стоимость кабеля с сечением k , у.е./км; l ^t _{( i , j )} – длина участка кабельной линии, выполненная кабелем с сечением k , км.; c_k – стоимость подключения группы ВЭУ к шинам подстанции, у.е; c k.d – стоимость дополнительного

a)

L=40,05 км

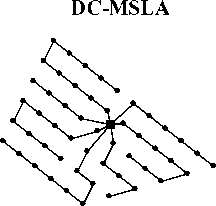
L=40,09 км

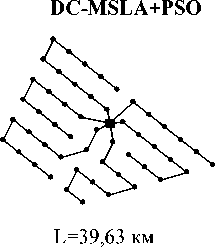
б)

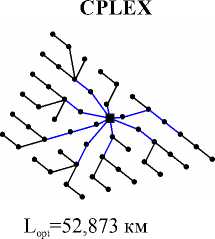
^ ВЭУ ■ ПС C=10

EW

DC-MSLA

L=61,70 км

P« ВЭУ ■ ПС C1=2  C2=7

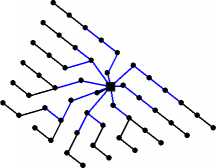
L=56,31 км

DC-MSLA+PSO

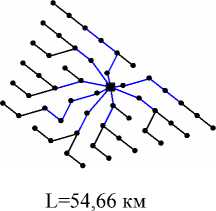
Рис. 4. Сравнение результатов построения схемы прокладки кабельных линий: a – неразветвленная конфигурация с кабелем одного типа; б – разветвленная сеть с кабелями двух типов ( С – проводимость кабеля, заданная числом турбин)

POS

DC-MSLA DC-MSLA +PSO

+PSO

Рис. 5. Распределение оценок эффективности сравниваемых алгоритмов: а – синтез магистральной схемы с одним типом кабеля, б – синтез магистральной разветвленной схемы с двумя типами кабелей

коммутационного оборудования ВЭУ, у.е.; n_k – число присоединений к шинам МТП; n_k.d – количество единиц дополнительной коммутационной аппаратуры ВЭУ.

Стоимость подключения группы ВЭУ к шинам подстанции и стоимость дополнительного комплекта коммутационной аппаратуры ВЭУ принимаются c k = 67,143 у.е. и c k.d = 24,74 у.е. [22].

Потери мощности в кабелях вычисляются по формуле

• ^{∆ P}kl ^{= 3} ∑ I (² i , j ) ^{⋅ r}k ^⋅ l^t ( i , j ) ^{,                    (12)}

(i, j,t)∈A где I(i, j) – ток на участке КЛ, А; rk – удельное активное сопротивление проводника, Ом/км.

Допустимый длительный ток I_d , удельное сопротивление r и стоимость c kl кабелей используемых сечений F сведены в табл. 3.

Таблица 3

Параметры кабелей [22, 23]

2 F ,мм	I d , A	r ,Ом/км	c kl , у.е./км
150	384	0,155	237,78
500	659	0,070	405,82

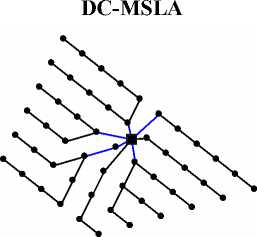
ВЭУ ПС     150 мм2    500 мм2

Рис. 6. Оптимизированные схемы ВЭС

Таблица 4

Технико-экономические показатели фактической и оптимизированных конфигураций МВЭС

Показатель	Фактическая схема	Алгоритм
		MSLA	DC-MSLA	DC-MSLA+PSO
Протяженность кабельных линий L , км	40,17	40,50	40,34	40,34
Стоимость кабелей, млн у.е.	10,65	10,87	10,43	10,43
Стоимость РУ МТП, млн у.е.	0,40	0,47	0,47	0,47
Стоимость РУ ВЭУ, млн у.е.	0,15	0,13	0,13	0,10
Стоимость системы сбора мощности, млн у.е.	11,21	11,47	11,03	11,00
Оценочные потери мощности в КЛ ΔPкл, МВт	1,032	0,962	0,915	0,992
Целевой показатель δ, у.е./МВтч	7,007	7,167	6,892	6,880

В качестве целевой функции гибридного алгоритма DC-MSLA+PSO используется соотноше- ние капитальных затрат на компоненты системы сбора мощности (11) к максимальному годовому производству электроэнергии:

5 =

С ccm

( P ins -Д Р и ) ■ 8760,

где P ins – установленная мощность ВЭС, МВт; A P_a - оценочные потери мощности в кабельных линиях, МВт.

Полученные в результате оптимизации схемы изображены на рис. 6.

Результаты оптимизации сведены в табл. 4.

Результаты показывают, что решения, полученные при использовании алгоритма (DC-MSLA), на 1,6 % экономичней по показателю целевой функции δ в сравнении с фактической схемой компоновки и на 3,8 % лучше результата оригинального алгоритма (MSLA). Комбинированный вариант (DC-MSLA+PSO) позволяет получить более качественное решение, что позволяет снизить целевой показатель на 1,8 %.

Заключение

В статье рассмотрена проблема синтеза топологии структурированной кабельной системы морских ветроэлектростанций с учетом стоимо- сти ее компонентов и технических ограничений. Предложен и протестирован метод синтеза, реализованный на основе модифицированного алгоритма (DC-MSLA) для аппроксимации задачи поиска дерева сети с минимальной стоимостью при выполнении ограничений на проводимость связей и степень узлов сети с учетом стоимости, зависящей от степени узлов и типа связей. Реализованный метод позволяет выполнять синтез схем прокладки кабельных путей неразветвленной и разветвленной конфигурации, выполняемых кабелями разных сечений, при этом выбирая лучший вариант по стоимости с ограничением затрат на дополнительное коммутационное оборудование. Для повышения качества решений реализован и протестирован гибридный алгоритм, реализованный путем добавления дополнительных варьируемых параметров в функцию компромиссных решений эвристического алгоритма DC-MSLA и использования метода роя частиц для поиска оптимальных параметров, что позволяет добиться улучшения конечного решения. В результате проведенных испытаний получены количественные оценки эффективности предложенных алгоритмов на основе сравнения полученных решений с результатами оптимизации, полученными при использовании ранее предложенных методик.