Оптимизация качества распознавания выбором допусков при обучении нейронной сети

При решении OCR-задач и, в частности, задач распознавания рукописных цифр широко используются нейронные сети [1]. Наиболее распространенным выбором является многослойный персептрон. К сожалению, с ростом количества признаков (что характерно для изображений) число нейронов быстро растет, и обучение персептрона становится довольно затратным. Заметим, что само по себе обучение нейронной сети не является самой сложной частью проблемы. Гораздо труднее найти сеть подходящей архитектуры, что требует многократного выполнения цикла обучения-тестирования. При этом актуальным является применение алгоритмов обучения, дающих наилучшую в некотором смысле (обычно по критерию качества распознавания) комбинацию параметров сети заданной архитектуры.

В настоящей работе рассматривается алгоритм обучения многослойного персептрона с использованием равномерного критерия качества обучения. В частности, исследуется возможность получения максимального качества распознавания путем адаптивной настройки параметров критерия на этапе обучения. Результаты иллюстрируются на примере задачи распознавания изображений арабских цифр.

преследует цель минимизировать отклонение выходов нейронов от желаемых значений в равномерном смысле: | d _i – y _i|→min.

Интерпретация выходного вектора происходит следующим образом. Пусть k – номер нейрона выходного слоя с максимальным выходным сигналом y k = max ( y i ) и c — некоторое действительное чис- i

ло. Если выполняется условие fУк > c, l У1 * к < - c,

то нейронная сеть распознала класс k . Иначе будем считать, что распознавание происходит неуверенно и, как следствие, вырабатывается решение об отказе от распознавания.

При наличии информации о принадлежности входного вектора l -му классу в (3) можно заменить k на l :

У i > c , y i -* i <  ^- c

Схема обучения нейронной сети

Для обучения используется алгоритм с отбором обучающих примеров, основанный на процедуре обратного распространения ошибки – поэтапное обучение [2].

Обозначим значения нейронов выходного слоя y i ( i =0..9 – по количеству распознаваемых цифр), а требуемые их значения для некоторого обучающего примера d i . В качестве активационной функции нейронов выходного слоя используется сигмоид

f ( s ) =

1 + exp

Поэтапное обучение, в отличие от классического градиентного метода и его модификаций [3], использующих среднеквадратичный критерий качества обучения

E = 1 £ ( y,- di)²,                       (2)

и считать, что при выполнении указанного условия нейронная сеть для заданного входного вектора выдает допустимый выходной вектор. При c >0 выполнение условия (4) будет означать выполнение условия (3) и правильное распознавание входного вектора ( k = l ). Выполнение условия (3) в ситуации, когда условие (4) не выполняется, приводит к ложному распознаванию ( k ≠ l ), а невыполнение (3) – к отказу от распознавания.

Величину c в (4) будем называть параметром допустимости . Очевидно, что при положительных значениях параметра выполнение условия (3) означает совпадение результата распознавания с интерпретацией ответа сети по правилу WTA (winner takes all). Для любого выходного вектора сети при изменении параметра c от -0,5 до 0,5 ответ нейронной сети будет сначала интерпретироваться как распознавание класса, а затем как отказ от распознавания.

Минимальное значение c , при котором нейронная сеть отказывается от распознавания, будем называть порогом допустимости для обучающего примера, а минимальное значение порога допустимости по всем обучающим примерам – порогом допустимости для данного обучающего множества.

При положительном значении порога допустимости нейронная сеть по правилу WTA распознает

все примеры правильно. Поэтому цель обучения – получить сеть с положительным порогом допустимости для обучающего множества. Обучение происходит поэтапно. На каждом этапе задается параметр допустимости c . Затем параметры нейронной сети корректируются по методу обратного распространения ошибок с использованием тех примеров, для которых выходной вектор сети не является допустимым. На каждом этапе значение параметра допустимости увеличивается до тех пор, пока не станет положительным и равным порогу допустимости обучающего множества.

Оценка качества распознавания

Для количественной оценки качества распознавания нейронной сети чаще всего определяют среднеквадратическое отклонение (2) по примерам тестового множества или подсчитывают долю неправильных распознаваний в тестовом множестве. В данном случае, мы различаем случаи неправильного распознавания и отказа от распознавания (отказ/ложное). При этом указанные критерии не позволяют учесть обычно большую опасность ложного распознавания по сравнению с отказом от распознавания.

Для оценивания качества распознавания будем использовать штрафную функцию вида

F=aлжnлж+aоткnотк, где nлж и nотк – соответственно, количество ложных распознаваний и отказов в тестовом множестве, а aлж и aотк – соответствующие весовые коэффициенты. Далее для весового коэффициента числа отказов в распознавании ограничимся случаем aотк=1. Для коэффициента ложных распознаваний будем рассматривать три варианта: aлж=1, 10 и 100.

Для сокращения записей далее штрафную функцию будем обозначать F N , где N – степень числа 10 в записи весового коэффициента ложного распознавания:

F N =10 ^N n лж + n отк . (5)

В указанном представлении F0 численно равно количеству неправильных распознаваний, F1 соответствует случаю малой, а F2 – большой «опасности» ложного распознавания.

Выбор варианта критерия зависит от конкретной задачи. Например, при распознавании индексов письменной корреспонденции в цифрочитающих устройствах автоматизированных письмосортировочных машин целесообразно использовать критерий F2, т.к. ошибки распознавания могут привести к отправке корреспонденции в регион, значительно удаленный от адресата.

При изменении величины параметра допустимости количество отказов и ложных распознаваний может меняться, т.е. в общем случае F N =F( N ,c). Следует заметить, что для активационной функции (1) при c=0,5 – первое, а при c=-0,5 – второе слагаемое в (5) равны нулю.

При уменьшении величины параметра допустимости по сравнению с 0,5 часть отказов в распознавании переходит в правильное распознавание, в ре- зультате значения штрафной функции уменьшаются. При увеличении параметра по сравнению с -0,5 ложные распознавания переходят отказы. Это свидетельствует о существовании минимального значения функции (5) при некотором промежуточном значении параметра допустимости.

Минимальное значение критерия (5) по множеству параметров допустимости будем использовать в качестве оценки качества распознавания:

GN = min F(N, c) , (6) c где N имеет тот же смысл и принимает такие же значения, как и в (5). Представляет интерес установить связь порога допустимости обучающего множества, получаемого в ходе обучения нейронной сети с оценкой качества распознавания (6).

В действительности, обучив персептрон до сколь угодно малого положительного порога допустимости, его можно увеличить, умножив веса нейронов выходного слоя на некоторое число α>1. Это справедливо для любой возрастающей нечетной активационной функции нейронов последнего слоя. При этом минимальное значение штрафной функции не изменится.

Дело в том, что при s 1 2 для (1) выполняется неравенство

f (αs 1 )< f (αs 2 ).

Это означает, что, несмотря на увеличение порогов допустимости примеров, отношения типа неравенств между ними сохранятся. Следовательно, сохранится и количество отказов и ложных распознаваний в (5) при величине параметра допустимости, равной порогу допустимости некоторого примера. Таким образом, множество значений штрафной функции сохранится, хотя изменятся значения аргументов, при которых они достигаются.

Результаты экспериментов

Проведенные эксперименты заключались в обучении нейронной сети до различных значений порога допустимости и вычислении оценки (5). Данными для обучения и тестирования являлись изображения арабских цифр, приведенные к размеру 12х16 пикселов. В качестве признаков использовались значения функции яркости (градация серого, 8 бит на пиксел). Таким образом, входной вектор имеет размерность 192, выходной – 10, по числу различных цифр. Исходное множество состояло из 48427 изображений печатных, стилизованных и рукописных цифр в примерной пропорции 30%, 30% и 40%, соответственно. Случайным образом 33000 изображений были отобраны в обучающее множество, оставшиеся составили тестовое множество.

Нейронная сеть обучалась до значений порога допустимости по обучающему множеству с 0,05 по 0,45 с шагом 0,05 и с 0,40 по 0,49 с шагом 0,01. Так как обучение нейронной сети начинается с генерации случайных значений весов, значения весов обученной сети так же имели случайный характер. Поэтому для количественной оценки качества обуче- ния проводилось усреднение по 48 эпизодам обучения, отличающимся начальными условиями. Значение критерия (6) вычислялось по тестовому множеству, не участвовавшему в обучении.

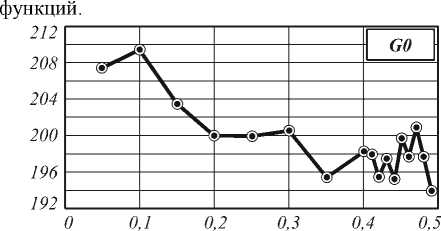
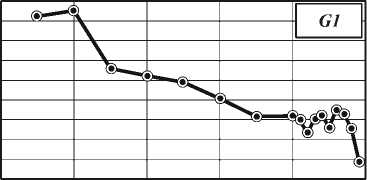
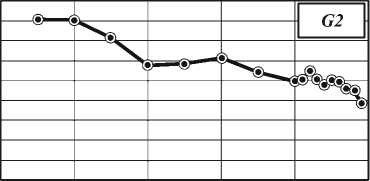
На рис. 1 показаны графики изменения критериев G0, G1 и G2 в зависимости от величины порогов допустимости, которые достигались в процессе обучения. Из графиков видно, что в целом при увеличении порога допустимости штрафная функция снижается, что говорит об улучшении качества распознавания обученной нейронной сети. Разница достигает 10% для всех трех функций.

При использовании нейронной сети в режиме распознавания для достижения малых значений штрафной функции необходимо знать минимальное достигнутое значение параметра допустимости. На рис. 2 приведены полученные в эксперименте зависимости минимальной величины параметра допустимости при увеличении порога допустимости обучающего множества для различных штрафных

О 0,1       0,2       0,3       0,4      0,5

О 0,1       0,2       0,3       0,4      0,5

Рис. 1. Зависимость штрафной функции от порога допустимости, достигнутого в процессе обучения

Для функции G0 получены отрицательные значения, что говорит о значительном превышении отказов распознавания над ложным распознаванием, т.к. при значении -0,5 отказов не может быть (условия (3) и (4) выполняются всегда). Для функции G1 все оптимальные значения допустимости для тестового множества меньше, а для функции G2 – больше, чем порог допустимости обучающего множества.

На графиках значений параметра допустимости можно выделить два участка: слабый линейный рост до значения аргумента 0,35-0,4, увеличивающийся в последующем. При этом снижение штрафной функции на втором участке незначительно, по сравнению с первым. На основании этого можно рекомендовать обучение нейронной сети до порога допустимости 0,35.

-0,40

-0,42

-0,44

-0,46

-0,48

-0,45

-0,35

-0,25

-0,15

0,5

0,4

0,3

0,2

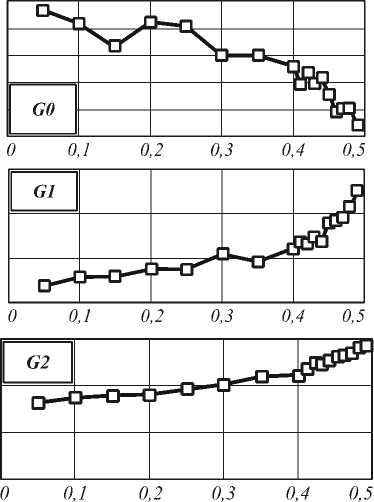
Рис. 2. Минимальное значение параметров допустимости для различных штрафных функций Таким образом, показана зависимость качества распознавания нейронной сети от одного параметра регулирующего процесс отбора данных. Варьированием этого параметра достигнуто 10%-е улучшение критерия качества, заданного в виде функции, учитывающей как ошибки, так и отказы при распознавании. Обоснован выбор значения параметра для обучения нейронной сети.

Работа выполнена при поддержке Министерства образования и науки РФ, правительства Самарской области и Американского фонда гражданских исследований и развития (CRDF Project SA-014-02) в рамках российско-американской программы «Фундаментальные исследования и высшее образование» (BRHE), а также при поддержке гранта Президента РФ № НШ-1007.2003.01 и гранта РФФИ № 05-01-08043.