Оптимизация коэффициента размытости ядра в задаче непараметрической идентификации

^* Идентификация многих стохастических объектов часто сводится к идентификации статических систем. Наиболее общая схема исследуемого дискретно-непрерывного процесса может быть представлена на рис. 1 [1–3; 5].

Рис. 1. Общая схема исследуемого процесса

На рис. 1 приняты обозначения: А – неизвестный оператор объекта; x ( t ) - выходной век

* © Михов Е. Д., Иванов Н. Д., 2018

тор процесса; u (t ) - вектор управляющих воздействий; ц (t ) - вектор входных не управляемых, но измеряемых переменных процесса; Л ( t ) - вектор входных неуправляемых и неизмеряемых переменных процесса; ξ ( t ) – случайное воздействие; ωⁱ ( t ): i =1, 2, …, k – переменные процесса, контролируемые по длине объекта; t – непрерывное время; H^µ , H^u , H^x , H^z , H^q , H^ω – каналы связи, соответствующие различным переменным и включающие в себя средства контроля, приборы для измерения наблюдаемых переменных; µ_t , u_t , x_t , ω_t – означает измерение в дискретное время; µ ( t ), u ( t ), x ( t ), ω ( t ), h^µ ( t ), h^u ( t ), h^x ( t ), h^ω ( t ) – случайные помехи измерений соответствующих переменных процесса. Процессы с дискретным снятием измерений часто встречаются в различных технических областях. С помощью подобных моделей проводится диагностирование компонентов электроники (диодов, резисторов и т.д.) на предмет брака. Подобная диагностика проводится при анализе компонентов элементной базы, используемых для сборки космических летательных аппаратов.

ОСМИЧЕСКИЕ АППАРАТЫ И

ТЕХНОЛОГ1Л1Л жада

Том 2

Уровни идентификации

Рассмотрим системы с различным уровнем априорной информации [4–6]:

где Ф (*) – это ядерная «сглаживающая» функция (2), а с_s ^x – коэффициент размытости ядра.

•

•

•

системы с параметрической неопределенностью. Параметрический уровень априорной информации предполагает наличие параметрической структуры модели и некоторых характеристик случайных помех, обычными из них являются нулевое математическое ожидание и ограниченная дисперсия. Для оценивания параметров используются чаще всего разнообразные итеративные вероятностные процедуры. При этих условиях также решается задача идентификации в узком смысле, как и во всех предыдущих случаях;

системы с непараметрической неопределенностью. Непараметрический уровень априорной информации не предполагает наличие модели, но требует наличие некоторых сведений качественного характера о процессе, например, однозначность, либо неоднозначность его характеристик, линейность для динамических процессов, либо характер его нелинейности. Для решения задач идентификации на этом уровне априорной информации (идентификация в широком смысле) применяются методы непараметрической статистики;

системы с параметрической и непараметрической неопределенностью. Важными с точки зрения практики являются задачи идентификации многосвязных систем в условиях, когда объем исходной информации не соответствует ни одному из вышеописанных типов. Например, для отдельных характеристик многосвязного процесса на основании физико-химических и энергетических закономерностей, закона сохранения массы, балансовых соотношений, могут быть выведены параметрические закономерности, а для других нет. Таким образом, мы находимся в ситуации, когда задача идентификации формулируется в условиях и параметрической, и непараметрической априорной информации. Тогда и модели представляют собой взаимосвязанную систему параметрических и непараметрических соотношений.

Ф ( o ) = <

1 - | o |, если | o | < 1, 0   , если1 < | o |.

Стоит сказать, что от выбранного вектора коэффициента размытости напрямую зависит качество построенной модели. Данный коэффициент определяет степень участия элементов выборки в оценке.

Коэффициент размытости ядра определяет степень участия элементов выборки в вычислении

в точке u_м (рис. 2).

А xs+1

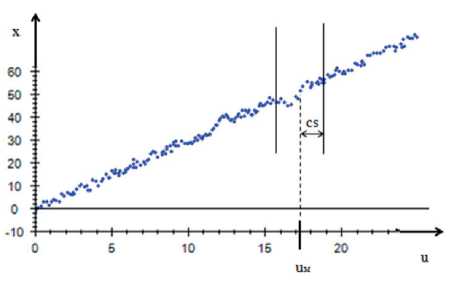
Рис. 2. Определение коэффициента размытости ядра

Как видно на рис. 2 участвуют в оценке в точке uм только те элементы выборки, у которых | n – n м | <  cs .

Исходя из большого влияния вектора cs на качество построенной модели у исследователей часто возникает задача оптимизации данного вектора (в качестве критерия оптимизации имеется ввиду точность построенной модели).

В настоящее время существуют множество методов оптимизации как для нахождения локальных экстремумов, так и для нахождения глобальных (хотя стоит сказать, что методы для нахождения глобальных экстремумов – вероятностные).

Ход исследования

Уровни идентификации

Непараметрическая идентификация пред ставляется в виде моделирования при помощи

ядерных оценок [7]: sk

X u (,), П Ф

Г и * u n , s + 1

—

u n,!

*

x s + 1 =

i = 1          j = 1

sk

ЕП Ф

i = 1 j = 1

x

I cL

*

u n , s + 1 — u,

z^

ny_

x

I    cs     J

Смысл исследования заключается в выяснении вопроса о необходимости оптимизации коэффициента размытости для каждого входного воздействия.

Для начала оптимизируем вектор коэффициента размытости ядра при помощи метода деформируемых многогранников. Слабостью данного метода можно считать то, что при нахождении минимума, он может «застрять» в локальном экстремуме. Для того чтобы определить, применим ли данный метод для оптимизации cs, построим графики зависимости среднеквадратичной ошибки ϭ от cs (рис. 3, 4).

В первую очередь были построены графики зависимости между коэффициентом размытости

Оптимизация коэффициента размытости ядра в задаче непараметрической идентификации ядра и среднеквадратичной ошибкой для двухмерного случая для различных процессов.

Характер данных зависимостей не изменялся. В качестве примера приведем один из графиков (рис. 3).

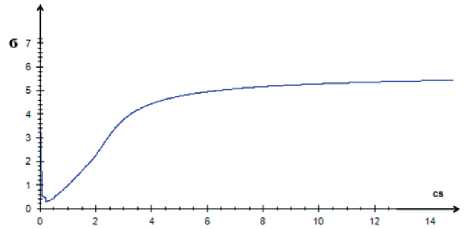
Рис. 3. Зависимость среднеквадратичной ошибки от коэффициента размытости ядра (2-мерный случай)

На рис. 3 отображено, что для 2-мерного случая зависимость является плавной и в ней не прослеживаются локальные минимумы.

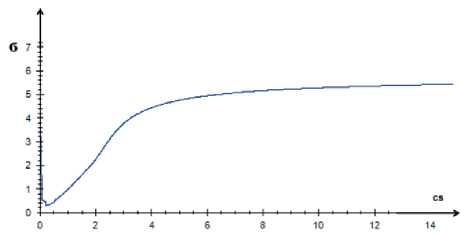
Рис. 4. Зависимость среднеквадратичной ошибки от коэффициента размытости ядра (3-мерный случай)

Также были построены графики зависимости между коэффициентом размытости ядра и среднеквадратичной ошибкой для трехмерного случая для различных процессов.

Характер данных зависимостей также не изменялся. В качестве примера приведем один из графиков (рис. 4).

На рис. 4 отображено, что для 3-мерного случая зависимость также является плавной и без локальных минимумов.

В связи с этим можно проводить оптимизацию cs при помощи метода деформируемого многогранника [8; 9].

После процесса оптимизации вектора коэффициентов размытости ядра при помощи метода деформируемого многогранника будет проведена оптимизация вектора коэффициентов размытости ядра при помощи генетического алгоритма [10].

Вычислительный эксперимент

Моделируемый процесс имеет два входных воздействия и один выходной параметр. Обучающая выборка была взята в количестве 300. Помеха, воздействующая на объект, была равна 7%. Критерием оптимизации была выбрана среднеквадратичная ошибка ϭ .

1 n —

° = X ( Xi- X )^{2 (3)} V n i = 1

Выведем результаты в виде табл. 1. Как мы можем видеть из табл. 1, оптимизация вектора коэффициента размытости занимает во много раз больше времени, чем оптимизация скалярного значения, при этом модель практически не становится лучше.

Также стоит отметить, что оптимизация при помощи метода деформируемых многогранников действует гораздо быстрее, чем оптимизация при помощи стандартного перебора или генетического алгоритма.

Было проведено сравнение между оптимизацией при помощи метода деформируемых многогранников, генетического алгоритма и оптимизацией при помощи стандартного перебора, где было доказано превосходство первого в задаче оптимизации вектора cs .

Таблица 1

Результаты оптимизации вектора cs

Метод оптимизации	Оптимизируемый параметр	Время нахождения оптимального cs , мс	Среднеквадратичная ошибка ϭ
Метод деформируемого многогранника	Вектор cs	1118	0,750869
Метод деформируемого многогранника	Скаляр cs	100	0,755853
Перебор возможных значений	Вектор cs	26808	0,780678
Перебор возможных значений	Скаляр cs	934	0,78102
Генетический алгоритм	Вектор cs	39067	0,758035
Генетический алгоритм	Скаляр cs	37028	0,761118

ОСМИЧЕСКИЕ АППАРАТЫ И технологии имина

Том 2

Заключение

Была рассмотрена общая схема исследуемого процесса. Был кратко проанализирован вопрос идентификация в «узком» и «широком» смыслах. Был рассмотрен вопрос оптимизации вектора коэффициентов размытости ядра. В статье были рассмотрены следующие алгоритмы оптимизации: метод перебора, метод деформиру- емого многогранника и генетический алгоритм. Перечисленные методы оптимизации были использованы для оптимизации вектора коэффициентов размытости ядра. Продемонстрировано, что нет необходимости в оптимизации коэффициента размытости ядра для каждого входного воздействия. Также продемонстрировано, что методы локальной оптимизации успешно решают задачу подбора коэффициентов размытости ядра.

Исследование выполнено за счет гранта Российского научного фонда ( проект №16-19-10089 ).