Оптимизация контура Азовского моря на основе алгоритма Рамера – Дугласа – Пекера

Одной из задач, возникающих при моделировании сложных природных систем, является задача построения гранично-адаптивной расчетной сетки. Азовское море является прибрежной системой и обладает сложной геометрией дна и береговой линии, характеризуется большим перепадом глубин, наличием песчаных кос. При построении треугольных сеток возникает проблема избыточной детализации полигональных моделей, что зачастую приводит к увеличению объема данных, что, в свою очередь, повышает нагрузку на вычислительные ресурсы, объем памяти и время обработки. Поэтому становится особенно актуальной задача оптимизации представления геометрии области вычислений при сохранении ее визуальной и топологической точности.

В данной статье для оптимизации контура расчетной области использована модификация алгоритма Рамера – Дугласа – Пекера (далее – РДП) [1]. Этот метод позволяет эффективно уменьшать количество точек в ломаных линиях и полигонах, сохраняя их основные геометрические особенности. Его главное преимущество заключается в гибкости: степень упрощения задается параметром ε, который определяет максимально допустимое отклонение.

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 2 за 2025 год

Другим известным методом упрощения контуров является метод Visvalingam – Whyatt, основанный на постепенном удалении наименее значимых треугольников, образованных соседними вершинами полилинии [2]. Удаляя последовательно точки, создающие наименьшую площадь треугольника, удается сохранить глобальные особенности формы и существенно уменьшить число вершин. Однако на больших объемах данных этот метод работает медленнее, чем алгоритм РДП. Также используется метод разбиения на кубические B-сплайны (Cubic Bezier Curves Decomposition) [3]. Вместо прямого удаления точек этот подход заменяет сегментированную линию гладкими сплайновыми кривыми (B-сплайнами). Вместо подбора отдельных точек методом строится непрерывная линия, близкая к оригиналу. Также широко применим векторный радиус-метод (RadiusBased Methods) [4]. Здесь определяется радиус вокруг каждой точки, который показывает максимальное удаление соседних точек. Если радиус меньше некоторого предела, точка считается незначимой и исключается. Этот подход эффективен для работы с зашумленными данными, такими как треки движения транспортных средств или пешеходов, и позволяет убрать лишние колебания траектории.

Построение и оптимизация контуров Азовского моря

Построение и анализ обработки упрощенных контуров производились на основе контура реального физического объекта сложной формы – Азовского моря. На контуре вдоль северного и северо-западного побережья хорошо заметно наличие песчаных кос. Размер отдельных кос достигает длины 20 и даже 40 км и в местах их расположения соответствует 10 и 25 % протяженности моря с севера на юг, так что их учет при моделировании различных показателей моря является важной задачей, позволяющей получать результаты, наиболее приближенные к наблюдаемым в природе явлениям.

Изображение полного контура

Для получения детального контура Азовского моря, включая координаты и форму кос, были использованы интеллектуальные технологии, в частности сверточная нейронная сеть U-Net в сочетании с методами компьютерного зрения из библиотеки OpenCV [5].

Подаваемый на вход алгоритмов контур Азовского моря состоит из 5353 вершин, расположенных на плоскости с координатами от 1147 до 5236 по оси X и от 0 до 2554 по оси Y . Далее этот контур будет называться полным, или исходным (см. Рисунок 1). Проведенный поверхностный анализ позволил сократить количество точек в три раза, не теряя при этом значимых геометрических характеристик Азовского моря, и получить контур из 1785 вершин. Далее такой контур будет называться прореженным, или мини-контуром.

Из-за особенностей работы алгоритмов библиотеки OpenCV, применяемой на последних этапах распознавания, наблюдаются характерные артефакты в структуре контуров. Как видно на Рисунке 2, полный контур на всем своем протяжении содержит многочисленные компактно расположенные группы точек, формирующие локальные кластеры высокой плотности. Плотные группы точек в дальнейшем могут быть заменены едиными репрезентативными точками без потери значимой информации об общей форме контура и ключевых геометрических особенностях.

Оптимизация контура Азовского моря на основе алгоритма Рамера – Дугласа – Пекера

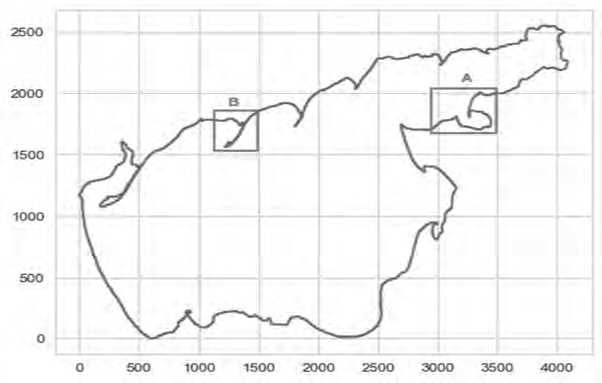
Рисунок 1. Детальный контур Азовского моря (зона А – зона демонстрации упрощения контура прореживанием; зона B – морская коса при упрощении которой алгоритмом РДП возникают самопересечения)

Источник: здесь и далее рисунки выполнены авторами.

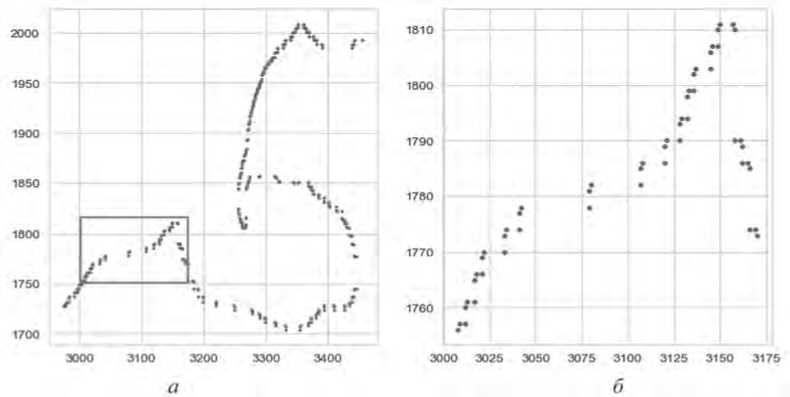
Рисунок 2. Артефакты первичного распознавания контура:

а – зона А из Рисунка 1; б – выделенный участок с хорошо заметным группированием точек

Упрощение контура

При формировании гранично-адаптивной сетки количество точек исходного контура, описывающего внешнюю границу моделируемой области, оказывает прямое влияние на общее количество узлов результирующей сетки, получаемой в результате триангуляции области, ограниченной контуром. Увеличение числа узлов сетки, в свою очередь, увеличивает вычислительные затраты и сложность численного моделирования.

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 2 за 2025 год

На данном этапе рассмотрим два неисключающих друг друга подхода:

• 1)    прореживание узлов исходного контура в соответствии с некоторым шаблоном;

• 2)    применение алгоритмов на основе алгоритма РДП [6; 7] для упрощения контуров.

Регулярное прореживание узлов контура

Одним из простых способов сокращения количества узлов (точек) исходного контура является его прореживание в соответствии с некоторым заданным шаблоном. Данный подход может оказаться одновременно эффективным, и, учитывая наличие в исходном контуре плотных групп точек, достаточно точно передающим форму исходного контура.

Поскольку большинство плотных групп состоят из трех узлов (см. Рисунок 2, б ), самым простым решением будет выборка из исходного (полного) контура каждого третьего узла. В такой ситуации прореженный контур (мини-контур) будет содержать 1785 узлов. Как видно из Рисунка 3, полученный таким образом контур в точности передает форму и особенности исходного контура, убирая локальные шумы, возникшие в ходе распознавания, что остается верным не только для зоны А, но и для всего контура, включая зоны узких морских кос.

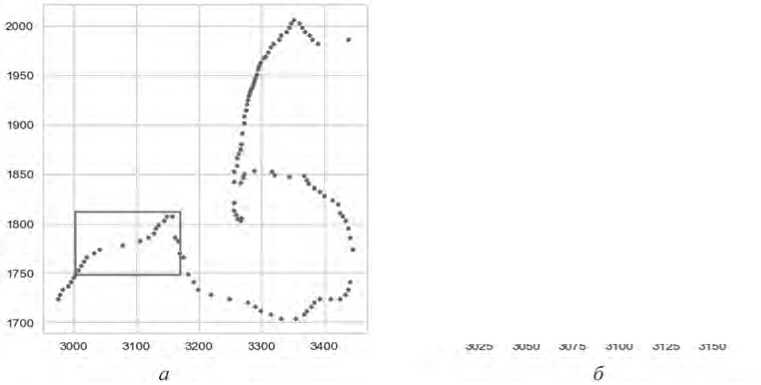
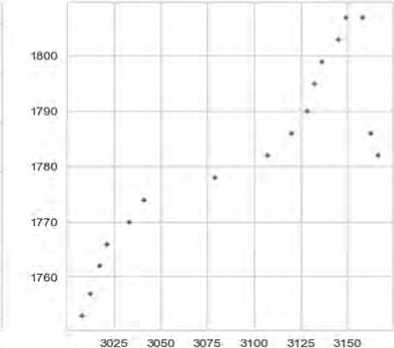
Рисунок 3. Упрощение исходного контура на основе прореживания:

а – упрощенная зона А из Рисунка 1; б – выделенная область после прореживания

Упрощение контура на основе алгоритма Рамера – Дугласа – Пекера

Построим ряд упрощенных контуров с использованием алгоритма РДП, варьируя величину допустимого отклонения от 2 до 10 единиц. Упрощение будем проводить как для полного контура, полученного на основе распознавания изображений Азовского моря, так и для прореженного мини-контура. Количество узлов (точек) для упрощенных контуров при различных значениях допустимого отклонения приведены на рисунке ниже. Как видно из графика (см. Рисунок 4), уже при значении допустимого отклонения в 5 единиц количество узлов, получаемых после применения алгоритма РДП, мало зависит от контура, подаваемого на вход алгоритма (полного или прореженного), а при значениях в 10 единиц становится практически одинаковым.

Оптимизация контура Азовского моря на основе алгоритма Рамера – Дугласа – Пекера

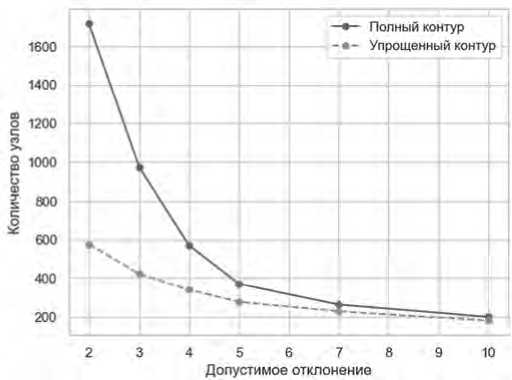
Рисунок 4. Зависимость количества узлов от параметра ε

Однако, несмотря на вычислительную простоту, алгоритм РДП не гарантирует сохранения топологии исходного контура. В процессе работы, особенно при обработке невыпуклых контуров и при относительно больших допустимых отклонениях, он может приводить к появлению самопересечений в результирующем контуре, которых не было в исходном. Например, на Рисунке 5 представлен участок зоны B, в котором алгоритм РДП при значениях допустимого отклонения больше 5 формирует самопересечение.

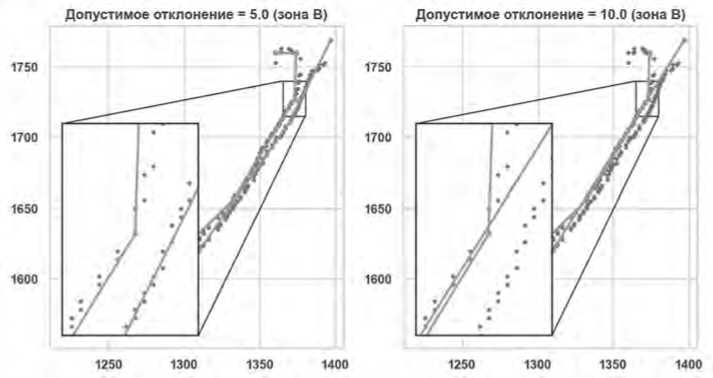
Рисунок 5. Зависимость наличия самопересечения контура от допустимого отклонения

Модификация алгоритма Рамера – Дугласа – Пекера с целью исключения самопересечений упрощенного контура

С целью исключения самопересечений в контуре, которые могут возникать после применения алгоритма РДП, была реализована постобработка упрощенных контуров.

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 2 за 2025 год

Предположим, что контур, подаваемый на вход алгоритма, является описанием границы мелководного водоема и не содержит самопересечений. Тогда при наличии самопересечений каждые два пересекающихся сегмента в упрощенном контуре образованы путем удаления узлов входного контура, и такое самопересечение можно устранить, вернув часть удаленных узлов в упрощенный контур.

Рассмотрим схематичное изображение части контура (см. Рисунок 6), описывающее оконечный участок морской косы (см. Рисунок 1, зона B) при упрощении которого получена последовательность сегментов (A,B) – (B,C) – (C,D) – (D,E).

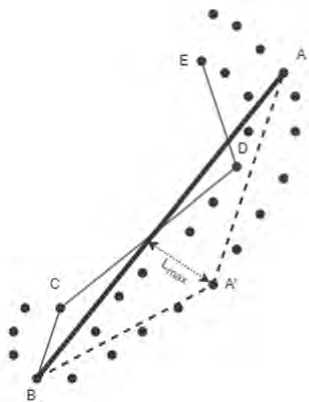
Рисунок 6. Постобработка упрощенных контуров

Из-за слишком большого допустимого отклонения и особенностей алгоритма РДП сегмент (A,B), полученный при упрощении, пересекает противонаправленную часть контура, образуя пересечения сегментов в парах (A,B) – (C,D) и (A,B) – (D,E). Возьмем первую пару и выберем в ней сегмент (A,B) как наиболее длинный (содержащий наибольшее количество удаленных узлов исходного контура). Сегмент (A,B) можно разбить на два отдельных сегмента (A,A’) – (A’,B), выбрав узел A’ так, чтобы его расстояние до сегмента (A,B) было максимальным из всех удаленных узлов, принадлежащих участку исходного контура между узлами A и B. Результат работы такого алгоритма для зоны B представлен на Рисунке 7.

Оптимизация контура Азовского моря на основе алгоритма Рамера – Дугласа – Пекера

Допустимое отклонение = 10.0 (зона В)

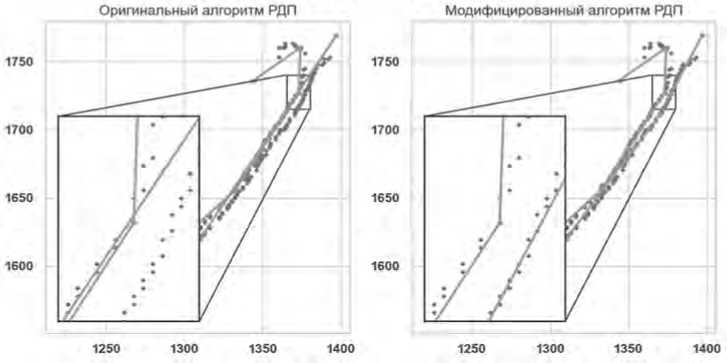
Рисунок 7. Устранение самопересечения упрощенного контура после постобработки

Формально описанный выше алгоритм устранения самопересечений для всего контура можно записать как

Algorithm RemoveSel(Intersections (Р, С)

С' ♦— С                       * рабочая копия контура

• 1    — RecalcIntersections(C') * список пересекающихся пар ребер iter*—0; lmax«—1000          ► защитное ограничение на итерации

while I # 0 and iter < Imax do iter *— iter + 1

((A,B),(C.D))«— first(l)         » берем первую пару пересеченных ребер

• ► выбираем ребро с большим количеством промежуточных точек if|B-A|>|D-C|then

u *— ChooscCandidateForSegment(A.B) ► попытка разбить ребро (А,В) Insert u in С' between A and В else v «— ChooseCandidateForSegment(C.D) ► попытка разбить ребро (C,D) Insert v in С' between С and D end if

I«— RccalcIntcrscctions(C')                 * пересчитываем пересечения end while return C'

end Algorithm

Заключение

Рассмотрена задача упрощения геометрических контуров с использованием алгоритма РДП для оптимизации обработки данных дистанционного зондирования. Разработан адаптивный подход к упрощению контуров, учитывающий особенности распределения точек в результатах обработки исходных изображений библиотекой OpenCV. Показана

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 2 за 2025 год эффективность комбинированного подхода (RDP + прореживание) для обработки протяженных географических объектов. Экспериментально подтверждена возможность сокращения количества точек на 60…80 % без потери значимых геометрических характеристик контура. В качестве практического примера рассмотрено построение упрощенного контура Азовского моря для ускорения обработки спутниковых снимков.

Полученные результаты имеют важное значение для задач оперативного мониторинга прибрежных систем, могут применяться для математического моделирования гидродинамических и гидробиологических процессов [8].

Исследование подтвердило, что сочетание алгоритма РДП с предварительной обработкой данных представляет собой эффективное решение для задач оптимизации векторных контуров в прикладных геоинформационных системах.