Оптимизация линейных систем с закрепленными концами траекторий и квадратичным функционалом при наличии ограничений

Введение. В наиболее известных работах в области моделирования и автоматического управления можно найти примеры удачной постановки и решения различных задач [1–4]. Многие задачи оптимального управления рассматриваются в двух постановках. Согласно одной из них оптимальное управление ищется как функция времени и начального состояния системы. Другая постановка задачи синтеза предполагает поиск оптимального управления в виде некоторой функции текущего состояния управляемой системы и времени.

В основе решения задач оптимального управления в первой постановке лежит принцип максимума Понтрягина [5] (решение сводится к соответствующей краевой задаче), а решение той же задачи во второй постановке основано на динамическом программировании (задача сводится к решению уравнения Беллмана [6]).

Разработка различных способов построения алгоритмов управления, обладающих необходимыми для приложений свойствами, является актуальной задачей современных информационных технологий [7].

В данной работе рассматривается постановка задачи оптимального управления, когда для управляемой системы задаются оба граничных условия. Предлагается конструктивный алгоритм управления, основанный на принципе обратной связи с учетом ограничений. Задача оптимального управления системами с закрепленными концами траекторий возникает, например, при исследовании динамики робототехнических и электроэнергетических систем, химических и ядерных реакторов. В простейшем случае динамика исследуемых систем может быть описана линейными дифференциальными уравнениями, критерием качества управления может служить квадратичный функционал.

Постановка задачи. Рассмотрим задачу об оптимальном управлении линейной нестационарной системой в соответствии с квадратичным критерием качества при наличии огра- ничений на управления. Если компоненты управляющего вектора не ограничены по величине, то для управляемой линейной системы можно найти аналитически оптимальные управления и оптимальные траектории.

Пусть управляемая система описывается системой дифференциальных уравнений x = A(t)x + B(t)u,     t E (t0,T);(1)

x(t0) = xо, x(T) = 0;  u(t) E U(t) = {u|a(t) < u(t) < в(t), t E (tо,T),(2)

а, в E C [ t о ,T ], a < 0, в > 0 }c L 2(( t о ,T), Rm),(3)

где x = x ( t ) — вектор состояния объекта управления размерности n х 1; u = u ( t ) — вектор управляющих воздействий размерности m х 1; A ( t ) , B ( t ) — заданные непрерывные и ограниченные матрицы размерности n х n и n х m соответственно; x 0 — заданный вектор.

Обозначим через A( 1 ₀ , T, x 0 ) множество всех допустимых управлений, удовлетворяющих условию u ( t ) E U ( t ) , t E ( t о ,T ) , и соответствующих траекторий x ( t, u ) системы (1) , определенных на отрезке t о < t < T , т. е. множество допустимых пар { x ( t ) , u ( t ) } :

A(tо, T, x0) = {(x, u): u(t) E U(t), x(t)= A(t)x(t) + B(t)u(t), tо < t < T, x (tо) = x0, x (T) = 0}.

Пусть на множестве (4) задан функционал

T

J(x, u) = 2 У [x*Q(t)x + u*R(t)u] dt, t0

где Q ( t ) , R ( t ) — заданные симметричные непрерывные и ограниченные матрицы размерности n х n и m х m соответственно, удовлетворяющие условиям Q ( t ) >  0 (неотрицательноопределенная), R ( t ) >  0 (равномерно положительно-определенная).

Предположим, что множество (4) не пусто и система (1) управляема, т. е. выполняется условие

T

G (t о ,T )= / t0

Ф( t о ,t ) B ( t ) B * ( t )Ф * ( t о ,t ) dt >  0 ,

где Ф(t,T) = 6(t)6 1(т); 6(t) — фундаментальная матрица решений системы, описываемой однородным дифференциальным уравнением z, = A (t) z.

Задача. Найти синтезирующее управление й ( x ,t, x 0 ,t _о ,T ) , такое что соответствующая ему пара ( x ( t ) , u ( t )) E A( t о ,T, x 0 ) (4) и доставляет минимальное значение функционалу (5).

Для решения поставленной задачи образуем вспомогательный функционал с применением множителей Лагранжа специального вида. Для этого добавим к функционалу (5) систему дифференциальных уравнений (1) с множителем А = K ( t ) x + q ( t ) и выражение Л 1 ( а — u ) + А 2 ( u — в ) , где А i >  0; А 2 >  0 . В результате получим функционал

T

I [2 x * Q ( t ) x + 2 u * R ( t ) u + ( K ( t ) x + q ( t )) * ( A ( t ) x + B ( t ) u — ic)+ t 0

+ A 1 ( x ,t )( a ( t ) — u ) + A 2 ( x ,t )( u — в ( t )) ] dt, (7)

где q = q ( t ) — векторная функция размерности n x 1; K = K ( t ) — симметричная положительно-определенная матрица размерности n x n .

Множитель A = K ( t ) x + q ( t ) снимает ограничения, налагаемые на допустимые пары { x ( t ) , u ( t ) } в виде системы дифференциальных уравнений (1), а функции { A i ( x ,t ) , A ₂ ( x ,t ) } — соответствующие ограничения, налагаемые на управления (3).

Для рассматриваемой задачи метод множителей Лагранжа (принцип освобождения от связей) состоит в следующем: исходная задача оптимального управления с ограничениями сводится к другой задаче без ограничений. При этом новая задача формулируется таким образом, чтобы ее решение являлось решением первоначальной задачи [8, 9].

Введем в рассмотрение следующие функции:

v ^{( x ,t} ) = 1 ^x * K ⁽ t ) ^x + ^x * q ⁽ t ) - ¹ q * ⁽ t ) W ^{( t,T} ) q ⁽ t ) , Iv = ^A = K ⁽ t ) ^x + q ⁽ t );      ⁽⁸⁾

2                   2                   d x

M ( x , u ,t ) = 2 x [ Q ( t ) + K ( t )] x + 2 u R ( t ) u + ( K ( t ) x + q ( t )) ( A ( t ) x + B ( t ) u )+

^{+ x} q ⁽ t ) - q ⁽ t ) W ⁽ t, T ) q ⁽ t ) - ₂ q ⁽ t ) W ⁽ t, T ) q ⁽ t )^{+ A} i ^{( a (} t ) - ^u )^{+ A} 2 ^{( u} - ^{в (} t )) • ⁽⁹⁾

Тогда, используя функции (8), (9), функционал L ( x , u ) (7) представим в следующем виде:

T

L ( x , u ) = v ( x ( 1 0 ) ,t 0 )

— v ( x ( T ) ,T ) + J M ( x , u ,t ) dt^ t 0

Решение задачи . Произведем выбор K, W, q , λ ₁ , λ ₂ таким образом, чтобы при каждом фиксированном t E ( 1 0 ,T ) функция M ( x , u ,t ) достигала наименьшего значения на паре ( 5с, u ) . Если при этом функция 5с удовлетворяет дифференциальному уравнению (1) при управлении й = u ( x ,t, x 0 ,t 0 ,T ) с условиями (2) , (3) , то такая пара (гс( t ) , ii( t )) является искомым решением поставленной задачи.

Методами дифференциального исчисления находим управление, обеспечивающее минимальное значение функции M ( x , u ,t ) из (10) в следующем виде:

г! = —R 1 ( t )[ B * ( t )( K ( t ) x + q ( t )) — A 1 + A 2 ] •

Обозначим ^ = —R- 1[—A 1 + A2], тогда синтезирующее управление принимает вид тс = —R- 1( t) B* (t)(K (t) x + q (t)) + Ф (x,t) •                         (11)

Множители A ₁ >  0 , A 2 >  0 определим таким образом, чтобы выполнялись условия

A 1 ( a ( t ) — u ) = 0 , A 2 ( u — в ( t )) = 0 •                           (12)

Для этого осуществим выбор λ ₁ , λ ₂ , ϕ следующим образом:

A 1 = —R ( t ) inf(0 , w ( x , t ) — a ( t )) , A 2 = —R ( t ) inf(0 , в ( t ) — w ( x , t )) ,          (13)

Ф(x, t) = — inf(0, w(x, t) — a(t)) + inf(0, в(t) — w(x, t)), где

w ( x , t ) = —R - 1 ( t ) B * ( t )( K ( t ) x + q ( t )) .                           (14)

Определим функцию M ( x , u ,t ) на управлении, задаваемом формулой (11). Подставляя управление (11) в выражение (9) и группируя подобные члены, получаем функцию

M ( x , й , t ) = ^ x * [ Q ( t ) + K ( t ) A ( t ) + A ( t ) K ( t ) - K ( t ) B ( t ) R - ¹ ( t ) B * ( t ) K ( t ) + K ( t )] x +

+2 ^ * R ( t ) ф + ( x - W ( t, T ) q ) * [ q + A * ( t ) q - K ( t ) B ( t ) R ^{- 1} ( t ) B * ( t ) q - W ^{- 1} ( t, T ) B ( t ) ф ] +

+ ( x - W ( t,T ) q ) * W ^{- 1} ( t,T ) B ( t ) ф - 2 q * [ W - W ( t,T ) A 1 ( t ) - A i ( t ) W ( t,T )+

+ B 1 ( t )] q + A 1 ( a ( t ) - U ) + A 2 ( U - в ( t )) . (15)

Осуществим выбор матриц K, W ( t,T ) и функции q ( t ) следующим образом:

• 1)    матрица K ( t ) удовлетворяет матричному дифференциальному уравнению

K = -KA(t) - A*(t)K + KB(t)R-1(t)B*(t)K - Q(t), K(to) = Ko;(16)

• 2)    матрица W ( t,T ) удовлетворяет матричному дифференциальному уравнению

W = W(t,T)A1(t) + Ai(t)W(t,T) - Bi(t), W(TT) = 0;(17)

• 3)    функция q ( t ) удовлетворяет дифференциальному уравнению

q = -A*(t)q + W-1(t,T)B(t)Ф(x,t), q(to) = W-1(to,T)x(to),(18)

где

A 1(t) = A(t) - B (t)R-1(t)B* (t)K(t), B 1(t) = B(t)R-1 (t)B* (t).(19)

Пусть существуют решения уравнений (16)–(18) и выполнены условия (12). Тогда значение функции (15) равно

M(x, 'u ,t) = 2 ф* (x, t)R(t) ф (x ,t).

Здесь учтено соотношение

x(t) = W(t,T)q(t), t G [to, T].(21)

Дифференциальные уравнения, определяющие закон движения для системы (1) с управлением - й ( x ,t ) = w ( x ,t ) + ф ( x ,t ) , представим в следующем виде:

эс = A 1(t)x - B 1(t)q + B(t)ф(x,t), x(to) = xo;(22)

• <1 = - A1 (t) q + W -1( t, T) B (t) ф (x,t), q (to) = W -1( to ,T) x (to).(23)

В результате минимальное значение функционала L ( x , u ) (10) равно

T

1                                   1                                1

L ( ас , u ) = - O k K ( t o ) x о + x ₀ q ( t о ) - -q ( t o ) W ( t о ,T ) q ( t o ) +      [ ^ ( x ,t ) R ( t ) ^ ( x ,t )] dt. (24)

^{2                          2                         2}

t 0

Покажем, что состояние системы (22), (23), соответствующее управлению (11), в конечный момент времени равно нулю, т. е. x ( T ) = 0 . В дифференциальных уравнениях (22), (23) обратим их линейные дифференциальные части и представим их в виде интегральных уравнений

t

t

x ( t ) = Ф( t,t о ) ( x 0 - У Ф( t 0 ,т)B 1 ( т) q ( т)dт + J Ф( t о ,т ) B ( т) у ( x ( т),т ) dт );     (25)

t 0

t 0

q ⁽ t ) = ^Ф * ⁽ t о ,t )

t q (t о) + У t0

Ф * ( т, t о ) W 1 ( т, T ) B ( т ) у ( x ( т ) , т ) dт

Здесь Ф( t,т ) = 6 ( t ) 6 1 ( т ) — матрица; 6 ( t ) — фундаментальная матрица решений системы, которая описывается однородным дифференциальным уравнением x = A 1 ( t ) x ; матрица A 1 ( t ) имеет вид (19) , а матрица

T

W ( t,T ) = У Ф( t,т ) B 1 ( т )Ф * ( t,т ) dт t

удовлетворяет дифференциальному уравнению (17) и невырождена при выполнении условия управляемости (6).

Из интегральных уравнений (25), (26) непосредственно находим, что состояние системы (22) удовлетворяет граничному условию x ( T ) = 0 .

Результаты, полученные для поставленной задачи, сформулируем в виде теоремы.

Теорема. Для оптимальности пары ( x ( t ) , U (t )) Е А( t _о ,T, x 0 ) в задаче (1)-(3), (5) необходимо и достаточно, чтобы:

• 1)    x ( t ) удовлетворяла системе дифференциальных уравнений

ас = Ai(t)x - Bi(t)q + B(t)^(x,t), x(tо) = xо;(28)

= - Ai (t) q + W - 1( t, T) B (t) ^ (x, t), q (t о) = W -1 (t о, T) x (t о);(29)

• 2)    управление й (t ) определялось по формуле

й( t) = u (x( t) ,t, x о ,t о ,T) = -R- 1( t) B* (t)(K (t):£( t) + q (t)) + ^ (:£( t) ,t),(30)

где матрица K ( t ) является решением уравнения (16) ; функция ^ ( x ,t ) имеет вид

^ ( x , t ) = — inf(0 , w ( x , t ) — a ( t )) + inf(0 , в ( t ) — w ( x , t )) ,

w(x, t) = -R- 1(t)B*(t)(K(t)x + q(t)).(31)

Доказательство. Необходимость следует из выражений (11)–(19). Для доказательства достаточности покажем оптимальность найденной допустимой пары ( x ( t ) , й (t )) , используя управление (11) и значение функционала (5). Значение функционала (5) имеет вид (24), в котором использованы решения дифференциальных уравнений (22), (23) и соотношения (20), (21).

Пусть ( x i ( t ) , u i ( t )) — произвольная допустимая пара, удовлетворяющая дифференциальному уравнению (1) с граничными условиями (2). Значение функционала (5) запишем в следующем виде:

J ( X 1 , U 1 ) = 2 x 0 к X о + x 0 q о

-

2 ^q * W ⁽ t о ^,T ) ^q o +

T

+1 [ 2( u i + R1 (t) в *(t)(к (t) x i + q)) *R (t)(u i + R- 1( t) b* (t)(к (t) x 1 + q))+ t0

+ ( x 1 - W ( t,T ) q ) * ( q + Л 1 ( t ) q ) ] dt. (32)

Учитывая, что x ( t ) = W ( t,T ) q ( t ) , t E [ t 0 ,T ] , получаем

J ( x 1 , U 1 ) =

2 ^x 0 ^{( K (} t о )⁺ W ^{1 (} t о ^,T )) ^x о ⁺ 2

[ [(u 1 + R-1(t)B* (t)(K(t)+ t0

+ W - ¹ ( t,T )) x 1 ) * R ( t )( u 1 + R ^{- 1} ( t ) B * ( t )( K ( t ) + W ^{- 1} ( t,T )) x 1 ) ] dt.

Используя значение функционала (24), (32), с учетом дифференциальных уравнений (28), (29), управления (30) и функции ^ ( x ,t ) (31) получаем

T

J ( x 1 , u 1 ) — J ( Ж , 'll

) = 2 / [ ( u 1 ⁺ R ^{1 (} t ) B * ( t )( ^K ( t ) ⁺ W - ^{1 (} t,T )) x 1 ) * R ( t )( u 1 +

t 0

+ R ¹ ( t ) B* ( t )( K ( t ) + W ¹ ( t,T )) x 1 ) — ф * ( ж ,t ) R ( t ) ф ( x , t ) ] dt >  0 .

Следовательно, J ( x , u ) = inf {J ( x , u ) , ( x , u ) E A( t о ,T, x o ) } .

Алгоритм решения задачи на ПК. Опишем удобный для реализации на ПК алгоритм решения задачи оптимального управления (1)–(5).

• 1.    Используя метод Рунге — Кутты, проинтегрировать систему дифференциальных уравнений (16), (17) для определения матриц K ( t ) и W ( t,T ) в интервале [ t о ,T ] с условиями K ( t о ) = K о и W ( T,T ) = 0 .

• 2.    Задать условия x ( 1 0 ) = x 0 , x ( T ) = 0 и вычислить q ( 1 0 ) = W ^{- 1} ( 1 0 , T ) x ( 1 0 ) .

• 3.    Используя метод Рунге — Кутты, проинтегрировать систему дифференциальных уравнений (28), (29) в интервале [ t о ,T ] , задав начальные условия x ( t о ) = x 0 , q ( t о ) = W ^{- 1} ( t о ,T ) x ( t о ) . В процессе интегрирования системы (28), (29) необходимо выдать на печать график оптимальной траектории гё( t ) и оптимального управления u ( t ) . Если необходимо провести расчеты для новых значений x ( t _о ) = x 0 , то повторить п.п. 2, 3.

Следует отметить, что K ₀ — произвольная симметричная положительно-определенная матрица размерности nxn . При задании различных начальных условий K ( 1 0 ) = K ₀ для матричного дифференциального уравнения (16) получаем различные матрицы K ( t ) и W ( t,T ) . Однако при этом получается одна и та же вектор-функция u ( t ) вида (30), поскольку задача имеет единственное решение. При вычислении вектор-функции q ( t ) по формуле (29) влияние матрицы K ( t ) компенсируется.

Пример. Рассмотрим задачу оптимального управления

T

J ⁽ u ) =

2 У [ x 1 + 2 x 2 + u 2 ] dt ’

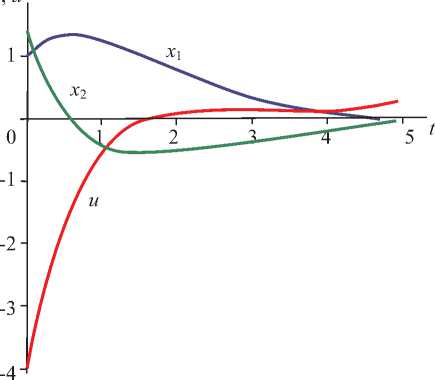
Рис. 1. График оптимального управления и оптимальных траекторий без ограничений на управления, соответствующий уравнениям (36)

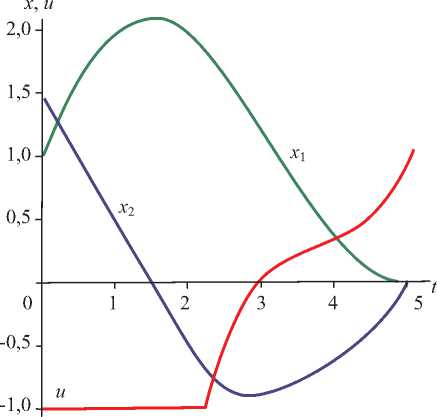
Рис. 2. График оптимального управления и оптимальных траекторий с учетом ограничений на управления, соответствующий уравнениям (37)

x 1 = x 2 , x 2 = u, x 1 (0) = 1 , x 2 (0)

2 , x 1 ( T ) = 0 , x 2 ( T ) = 0 , T = 5;

|u ( t ) | <  1 , t E [0 , 5] .

Решение задачи без ограничений на управления. Дифференциальные уравнения с управлением, определяющие закон движения системы (34) и доставляющие минимальное значение функционалу (33), представим в следующем виде:

xi = x2, x2 = —xi - 2x2 - q2, qi = q2, q2 = —q 1 + 2q2,

u — —x 1 — 2 x 2 — q 2 , K —

Решение задачи с ограничением на управления вида (35). Дифференциальные уравнения с управлением, определяющие закон движения системы (34) и доставляющие минимальное значение функционалу (33) , представим в следующем виде:

x 1 = x 2, x 2 = —x 1 — 2 x 2 — q 2 + у, q1 = q 2,  <12 = —q 1 + 2 q 2 + W 1У,                           (37)

u = w(x, t) + у (x, t), w(x, t) = —x 1 — 2x2 — q2, у (x, t) = — inf(0,w(x, t) + 1) + inf(0, 1 — w(x, t)).

Расчеты проводились на ПК с использованием пакета прикладных программ Maple-7, в котором реализован изложенный выше алгоритм решения задачи оптимального управления (33)–(35). На рис. 1 приведены графики оптимальных траекторий движения системы и управления без ограничений, на рис. 2 — с учетом ограничений на управления.

Заключение. Предложен новый подход построения синтезирующего управления (30), основанного на принципе обратной связи, приводящем динамическую систему в требуемое состояние за конечное время при наличии ограничений на управления. Оптимальный закон движения рассматриваемой системы с заданными граничными условиями определен в виде (28), (29). Разработан алгоритм решения задачи оптимального управления на ПК. Этот алгоритм реализован на примере (33)–(35). Полученный результат позволяет построить функцию Беллмана — Кротова в следующем виде:

T

2 x ( к ( t ) + w ¹

V ( x ,t )

⁽ t, T )) x + I [j⁽ A 1 ( x ,^T ) - A 2 ⁽ x ^,T )) * R - ^{1 ( T )(} A 1 ( ^{x ,T} ) - A 2 ^{( x ,T ))+}

+ A i ( x ,t )( u - a ( т )) + A 2 ( х ,т )( в ( т ) - u ) ] dT.